
Wetenschap
Onderzoekers beantwoorden fundamentele vraag over kwantumfysica
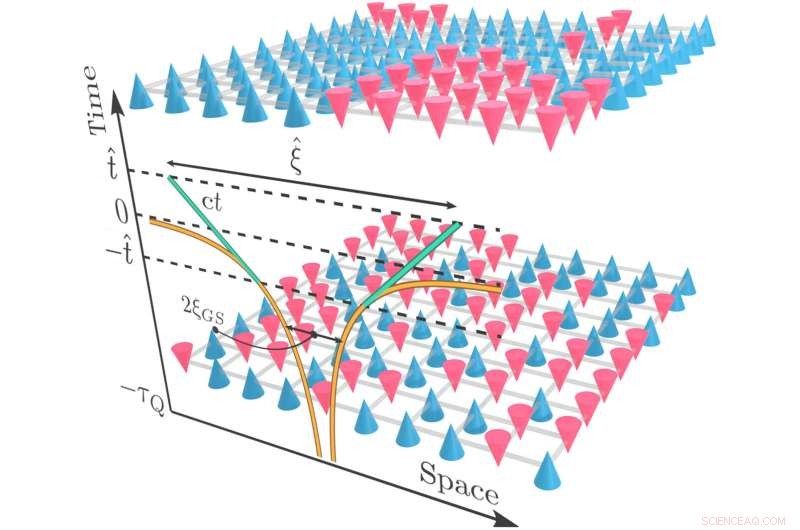
Schematische weergave van de dynamiek over een faseovergang in een tweedimensionaal spin-1/2 model. In de initiële paramagnetische toestand (onder) zijn spins uitgelijnd met de richting van het transversale magnetische veld. Een meting van de spinconfiguratie in die toestand langs de ordeningsrichting zou dan typisch een willekeurig patroon opleveren van spins die naar boven wijzen (blauwe kegels) of naar beneden (rode kegels). Na een langzame helling over een kwantumkritisch punt, ontwikkelt het systeem een kwantumsuperpositie van ferromagnetische domeinen, die, bij het meten van spinconfiguraties langs de ordeningsrichting, typisch een ineenstorting op een mozaïek van dergelijke domeinen zal opleveren (boven). Op de voorkant nemen we de groei van het ferromagnetische correlatiebereik op als functie van de tijd t vanaf t =−τQ naarmate de helling vordert over het kritieke regime met het kritieke punt op t =0. De genezingslengte ξˆ die de grootte van domeinen in het Kibble-Zurek (KZ) -mechanisme bepaalt, wordt ingesteld op het karakteristieke tijdstip ∣∣t∣
Een internationaal team van natuurkundigen, met medewerking van de Universiteit van Augsburg, heeft voor het eerst een belangrijke theoretische voorspelling in de kwantumfysica bevestigd. De berekeningen hiervoor zijn zo complex dat ze tot nu toe zelfs voor supercomputers te veeleisend zijn gebleken. De onderzoekers slaagden er echter in om ze aanzienlijk te vereenvoudigen met methoden uit het veld van machine learning. De studie verbetert het begrip van fundamentele principes van de kwantumwereld. Het is gepubliceerd in het tijdschrift Science Advances .
De berekening van de beweging van een enkele biljartbal is relatief eenvoudig. Het voorspellen van de banen van een groot aantal gasdeeltjes in een vaartuig die voortdurend botsen, vertragen en afbuigen, is echter veel moeilijker. Maar wat als het helemaal niet duidelijk is hoe snel elk deeltje precies beweegt, zodat ze op elk moment talloze mogelijke snelheden zouden hebben, die alleen verschillen in hun waarschijnlijkheid?
De situatie is vergelijkbaar in de kwantumwereld:kwantummechanische deeltjes kunnen zelfs alle potentieel mogelijke eigenschappen tegelijk hebben. Dit maakt de toestandsruimte van kwantummechanische systemen extreem groot. Als je wilt simuleren hoe kwantumdeeltjes met elkaar interageren, moet je rekening houden met hun volledige toestandsruimten.
"En dat is buitengewoon complex", zegt prof. dr. Markus Heyl van het Institute of Physics van de Universiteit van Augsburg. "De rekeninspanning neemt exponentieel toe met het aantal deeltjes. Met meer dan 40 deeltjes is het al zo groot dat zelfs de snelste supercomputers het niet aankunnen. Dit is een van de grote uitdagingen van de kwantumfysica."
Neurale netwerken maken het probleem beheersbaar
Om dit probleem te vereenvoudigen, gebruikte de groep van Heyl methoden uit het veld van machine learning:kunstmatige neurale netwerken. Hiermee kan de kwantummechanische toestand opnieuw worden geformuleerd. "Dit maakt het beheersbaar voor computers", legt Heyl uit.
Met behulp van deze methode hebben de wetenschappers een belangrijke theoretische voorspelling onderzocht die tot nu toe een uitstekende uitdaging is gebleven:het kwantum Kibble-Zurek-mechanisme. Het beschrijft het dynamische gedrag van fysieke systemen bij wat een kwantumfaseovergang wordt genoemd. Een voorbeeld van een faseovergang vanuit de macroscopische en meer intuïtieve wereld is de overgang van water naar ijs. Een ander voorbeeld is het demagnetiseren van een magneet bij hoge temperaturen.
Als je andersom gaat en het materiaal afkoelt, begint de magneet zich weer te vormen onder een bepaalde kritische temperatuur. Dit gebeurt echter niet gelijkmatig over het hele materiaal. In plaats daarvan worden tegelijkertijd veel kleine magneten met verschillend uitgelijnde noord- en zuidpolen gemaakt. De resulterende magneet is dus eigenlijk een mozaïek van veel verschillende, kleinere magneten. Natuurkundigen zeggen ook dat het gebreken bevat.
Het Kibble-Zurek-mechanisme voorspelt hoeveel van deze defecten te verwachten zijn (met andere woorden, uit hoeveel minimagneten het materiaal uiteindelijk zal bestaan). Wat vooral interessant is, is dat het aantal van deze defecten universeel is en dus onafhankelijk van microscopische details. Dienovereenkomstig gedragen veel verschillende materialen zich precies identiek, zelfs als hun microscopische samenstelling compleet anders is.
Het Kibble-Zurek-mechanisme en de vorming van sterrenstelsels na de oerknal
Het Kibble-Zurek-mechanisme werd oorspronkelijk geïntroduceerd om de vorming van structuur in het universum te verklaren. Na de oerknal was het universum aanvankelijk volledig homogeen, wat betekent dat de gehoste materie perfect gelijkmatig verdeeld was. Lange tijd was het onduidelijk hoe sterrenstelsels, zonnen of planeten uit zo'n homogene toestand konden zijn ontstaan.
In dit verband biedt het Kibble-Zurek-mechanisme een verklaring. Terwijl het universum afkoelde, ontwikkelden zich defecten op dezelfde manier als magneten. Inmiddels zijn deze processen in de macroscopische wereld goed begrepen. Maar er is één type faseovergang waarvoor het nog niet mogelijk is geweest om de geldigheid van het mechanisme te verifiëren, namelijk de eerder genoemde kwantumfaseovergangen. "Ze bestaan alleen bij het absolute nulpunt van -273 graden Celsius", legt Heyl uit. "Dus de faseovergang vindt niet plaats tijdens afkoeling, maar door veranderingen in de interactie-energie - je zou misschien kunnen denken aan het variëren van de druk."
Zo'n kwantumfase-overgang hebben de wetenschappers nu op een supercomputer gesimuleerd. Zo konden ze voor het eerst aantonen dat het Kibble-Zurek-mechanisme ook in de kwantumwereld van toepassing is. "Dat was geenszins een voor de hand liggende conclusie", zegt de natuurkundige uit Augsburg. "Onze studie stelt ons in staat om de dynamiek van kwantummechanische systemen van veel deeltjes beter te beschrijven en zo de regels die deze exotische wereld beheersen nauwkeuriger te begrijpen." + Verder verkennen
Nieuwe vacht voor de kwantumkat:verstrengeling van veel atomen voor het eerst ontdekt
 Onderzoekers smeden nieuwe rekenhulpmiddelen om nauwkeuriger voorspellingen te doen van eiwitstructuren
Onderzoekers smeden nieuwe rekenhulpmiddelen om nauwkeuriger voorspellingen te doen van eiwitstructuren Onderzoekers ontdekken nieuwe structuur voor veelbelovende materiaalklasse
Onderzoekers ontdekken nieuwe structuur voor veelbelovende materiaalklasse Nieuw ontwikkeld materiaal kan leiden tot lichtere, veiliger auto-ontwerpen
Nieuw ontwikkeld materiaal kan leiden tot lichtere, veiliger auto-ontwerpen Nieuwe aanpak voor het opvangen van gas bevordert het beheer van nucleaire brandstof
Nieuwe aanpak voor het opvangen van gas bevordert het beheer van nucleaire brandstof Voedselkwaliteitscontrole sneller en gemakkelijker gemaakt
Voedselkwaliteitscontrole sneller en gemakkelijker gemaakt
 Wetenschappers volgen een lekkage van lading van New York naar Noorwegen, onthullen hoe stromen schadelijke stoffen verspreiden
Wetenschappers volgen een lekkage van lading van New York naar Noorwegen, onthullen hoe stromen schadelijke stoffen verspreiden Een nieuwe manier om verontreinigingen uit nucleair afvalwater te verwijderen
Een nieuwe manier om verontreinigingen uit nucleair afvalwater te verwijderen Geconfronteerd met hoge smogniveaus, Milaan gaat auto's zondag verbieden
Geconfronteerd met hoge smogniveaus, Milaan gaat auto's zondag verbieden De koolstofeconomie transformeren
De koolstofeconomie transformeren Australische klimaattool identificeert einde winter in 2050
Australische klimaattool identificeert einde winter in 2050
Hoofdlijnen
- Nest van bedreigde reuzenweekschildpad gevonden in Cambodja
- Wat zijn de kleine delen van het DNA die Code for a Trait?
- Verspilde vogelveren veranderd in voedsel
- Garnalenvisserij in New England voor minstens een jaar gesloten
- Onderzoekers identificeren een paar receptoren die essentieel zijn voor de communicatie tussen mannen en vrouwen bij planten
- Honden zijn expressiever als iemand kijkt
- Hoe nauwkeurig is ons mentale beeld van onszelf?
- Europa's oudste boom groeit nog steeds
- 245 miljoen jaar oude fossielen bieden nieuwe inzichten in de evolutie en voedingsstrategieën van waterinsecten
- Verduidelijking van het mechanisme voor het onderdrukken van turbulentie door ionenmassa
- Uw koelkast op zonne-energie laten werken

- Waarneming van niet-triviale supergeleiding op het oppervlak van type II Weyl-halfmetaal

- De groei van een organisme rijdt op een patroon van golven

- Fermilab-wetenschappers gaan op zoek naar donkere materie met behulp van kwantumtechnologie

 Nieuwe microscooptechniek onthult details van druppelkiemvorming
Nieuwe microscooptechniek onthult details van druppelkiemvorming Nieuwe studie suggereert dat harde eierschalen minstens drie keer zijn geëvolueerd in de stamboom van dinosauriërs
Nieuwe studie suggereert dat harde eierschalen minstens drie keer zijn geëvolueerd in de stamboom van dinosauriërs Nieuwe verfrommeling van hybride nanostructuren verhoogt de gevoeligheid van SERS
Nieuwe verfrommeling van hybride nanostructuren verhoogt de gevoeligheid van SERS Teachable Machine 2.0 breidt machine learning-ervaring uit
Teachable Machine 2.0 breidt machine learning-ervaring uit NASA bereidt zich voor om mensen terug naar de maan te sturen
NASA bereidt zich voor om mensen terug naar de maan te sturen  Mosgenoomonderzoek identificeert twee nieuwe soorten
Mosgenoomonderzoek identificeert twee nieuwe soorten Afbeelding:Musa Bay gevangen genomen door Copernicus Sentinel-2A
Afbeelding:Musa Bay gevangen genomen door Copernicus Sentinel-2A Wetenschappers maken cellen die de tastzin mogelijk maken
Wetenschappers maken cellen die de tastzin mogelijk maken
- Elektronica
- Biologie
- Zonsverduistering
- Wiskunde
- French | Italian | Spanish | Portuguese | Swedish | German | Dutch | Danish | Norway |

-
Wetenschap © https://nl.scienceaq.com

