Wetenschap
Mijn promotor heeft zojuist de Nobelprijs voor natuurkunde gewonnen - hier is hoe zijn onderzoek naar complexe systemen de wetenschap veranderde

In dit voorbeeld, een hoek van de driehoek is gefrustreerd. Credit:Johan Jarnestad/De Koninklijke Zweedse Academie van Wetenschappen, CC BY-NC
De Nobelprijs voor natuurkunde voor 2021 is gezamenlijk toegekend aan de Italiaanse Giorgio Parisi, De Japanse Syukuro Manabe en de Duitse Klaus Hasselmann voor hun "baanbrekende bijdragen aan ons begrip van complexe systemen".
Toen ik het nieuws hoorde, Ik kon het bijna niet geloven. Ik studeerde voor mijn masterscriptie en mijn Ph.D. in theoretische natuurkunde bij professor Parisi aan de Sapienza Universiteit in Rome.
Als ik zeg dat ik in ongeloof was, begrijp me niet verkeerd. Van alle mensen die ik ooit heb ontmoet tijdens mijn onderzoekservaring - misschien in mijn leven - is hij zonder twijfel de meest vindingrijke. Ik was dus niet verbaasd over het besluit van het Nobelprijscomité om hem tot laureaat te benoemen. Liever, het was hun beslissing om zijn "bijdragen aan ons begrip van complexe systemen" te erkennen die mijn interesse wekte.
Deze prijs voor professor Parisi, gesplitst met baanbrekende meteorologen Professor Manabe en Professor Hasselmann, is een verbazingwekkende erkenning van een heel onderzoeksgebied - misschien iets minder glamoureus dan de algemene relativiteitstheorie of snaartheorie - dat probeert te begrijpen en te modelleren wat we in de natuurkunde 'complexe systemen' noemen.
Deze omvatten zaken als klimaatecosystemen, financiële systemen, en biologische verschijnselen, om er een paar te noemen. De enorme verscheidenheid aan complexe systemen - vertegenwoordigd in fluctuerende markten en stromende spreeuwen - maakt het erg moeilijk om enige vorm van universele regels voor hen af te leiden. Dankzij het werk van Parisi hebben we ongekende conclusies kunnen trekken over systemen die, op het oppervlak, kijk willekeurig, onvoorspelbaar en onmogelijk theoretisch te modelleren.
In tegenstelling tot sommige andere natuurkundige modellen, complexe systemen zijn geen verzameling identieke deeltjes, regelmatig met elkaar omgaan op een manier die consistent en voorspelbaar is. In plaats daarvan, complexe systemen zijn systemen van elementen, mogelijk van elkaar verschillen, interactie op verschillende en schijnbaar onvoorspelbare manieren terwijl ze worden blootgesteld aan wisselende externe omstandigheden.
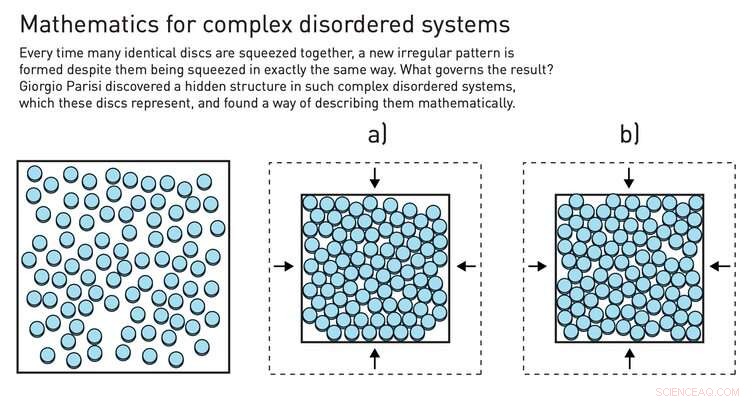
De replicatruc kan worden uitgevoerd door ballen in een doos te comprimeren. Credit:Johan Jarnestad/De Koninklijke Zweedse Academie van Wetenschappen, CC BY-NC
Een springplank voor het modelleren van complexe systemen is de theorie van "ontregelde systemen". Dit zijn in wezen systemen waarin verschillende paren elementen verschillende, potentieel tegenstrijdige krachten die ertoe kunnen leiden dat de elementen "gefrustreerd" raken.
Een manier om dit te illustreren is om je een partij (een gesloten sociaal systeem) voor te stellen, waar Alice misschien met Bob wil chatten, en Bob wil misschien met Charlie praten, maar Charlie wil misschien niet met Alice praten. Er is frustratie hier - dus wat moeten ze doen?
Het onderzoek van professor Parisi verduidelijkte wat er gebeurt als frustratie optreedt in wanordelijke en complexe systemen. Hij stelde vast dat complexe systemen in staat zijn hun trajecten in de tijd te onthouden, en kan lange tijd in suboptimale toestanden blijven steken.
In ons partijvoorbeeld stel je voor Alice, Bob, Charlie, en andere gasten die onregelmatig van gespreksgroepen en partners wisselen, in de hoop de beste groep mensen te vinden om mee te chatten, maar mogelijk nooit te vinden. Dat is de suboptimale toestand waarin complexe systemen kunnen blijven steken.
Patronen van wanorde
Een van de vele theoretische hulpmiddelen die professor Parisi heeft gebruikt om zijn theorie vast te stellen, is de zogenaamde "replicatruc" - een wiskundige methode waarbij een ongeordend systeem, herhaalt het meerdere keren, en vergelijkt hoe verschillende replica's van het systeem zich gedragen. Je kan dit doen, bijvoorbeeld, door knikkers in een doos samen te persen, die elke keer dat u de compressie uitvoert een andere configuratie zal vormen. Na vele herhalingen, Parisi wist het, vertellende patronen kunnen ontstaan.
Deze methode is nu een van de weinige theoretische pijlers voor de ontwikkeling van de hele theorie van complexe systemen zoals we die nu kennen. Het is aangetoond dat de theorie van professor Parisi betrouwbare voorspellingen geeft over de statistische eigenschappen van complexe systemen, variërend van onderkoelde vloeistoffen (vloeistoffen onder hun stollingstemperatuur), bevroren vloeistoffen, amorfe vaste stoffen zoals glas, en zelfs zwermen spreeuwen.
De theorie van wanordelijke systemen stelt ons in staat om de prachtige opkomst van coherente vluchtpatronen binnen dichte zwermen vogels te begrijpen - die erin slagen bij elkaar te blijven en ondanks ongunstige omstandigheden enorme groepen te vormen.
Hetzelfde raamwerk is gebruikt om het klimaat op aarde te begrijpen. De meteorologen die de Nobelprijs delen met professor Parisi zullen hebben vertrouwd op doorbraken in de theoretische natuurkunde om de modellen te produceren die we nu gebruiken om de opwarming van de aarde betrouwbaar aan te tonen.
Ik had de kans om deze onderwerpen te bespreken met professor Parisi in Rome, terwijl zijn experimenten met zwermen vogels plaatsvonden en tijdens zijn computersimulaties over het gedrag van glas. Een beetje van zijn verstand kennende, Het verbaast me helemaal niet dat hij de Nobelprijs voor natuurkunde heeft gekregen.
Maar ik ben aangenaam verrast dat het gebied van complexe systemen, die stilletjes de grens van theoretisch onderzoek in de natuurkunde verdringt, deze blootstelling heeft gekregen. Deze Nobelprijs heeft nieuwe legitimiteit opgeleverd - en, we kunnen hopen, nieuwe geesten - op dit fascinerende gebied van de hedendaagse natuurkunde.
Dit artikel is opnieuw gepubliceerd vanuit The Conversation onder een Creative Commons-licentie. Lees het originele artikel. 
 Leuke experimenten voor het scheiden van mengsels
Leuke experimenten voor het scheiden van mengsels  Onderzoekers bieden overzicht van samengestelde metaalschuimen en mogelijke toepassingen
Onderzoekers bieden overzicht van samengestelde metaalschuimen en mogelijke toepassingen Modificatie van aminozuren biedt nieuw startpunt voor ontwikkeling van medische behandelingen
Modificatie van aminozuren biedt nieuw startpunt voor ontwikkeling van medische behandelingen Kijken naar een toekomst waarin het ontdooien van vliegtuigen tot het verleden behoort
Kijken naar een toekomst waarin het ontdooien van vliegtuigen tot het verleden behoort Van receptorstructuur tot nieuwe osteoporosemedicijnen
Van receptorstructuur tot nieuwe osteoporosemedicijnen
 Pogingen om de in gevaar gebrachte Pando te herstellen, tonen belofte
Pogingen om de in gevaar gebrachte Pando te herstellen, tonen belofte De meeste aardverschuivingen in het westen van Oregon veroorzaakt door hevige regenval, geen grote aardbevingen
De meeste aardverschuivingen in het westen van Oregon veroorzaakt door hevige regenval, geen grote aardbevingen Het derde klimaatrapport van Oregon toont aan dat de staat nog steeds aan het opwarmen is, ondanks de koude winter
Het derde klimaatrapport van Oregon toont aan dat de staat nog steeds aan het opwarmen is, ondanks de koude winter Voor de wereldwijde watercrisis, klimaat kan de laatste druppel zijn
Voor de wereldwijde watercrisis, klimaat kan de laatste druppel zijn algen, zeewier verkleurt de wateren en stranden van Florida
algen, zeewier verkleurt de wateren en stranden van Florida
Hoofdlijnen
- Waarom zijn de Neanderthalers uitgestorven?
- Roofzuchtige bacteriën die patrijspoorten maken en fresco's schilderen in schadelijke bacteriën
- Welke Organelle vormt de basis voor Cilia en Flagella?
- Verschil tussen een gesloten en open bloedsomloop
- De voor- en nadelen van grote oren voor vleermuissoorten
- Rangschikken met behulp van een vierkantswortelcurve
- Make-up & Science Fair Ideas
- Welke materialen kan ik gebruiken om een DNA-model te maken?
- Vleermuizen anticiperen op optimale weersomstandigheden
 Onderzoekers verminderen de tijd die nodig is voor 3D-printen van glas en keramiek sterk
Onderzoekers verminderen de tijd die nodig is voor 3D-printen van glas en keramiek sterk ChipScope – een nieuwe benadering van optische microscopie
ChipScope – een nieuwe benadering van optische microscopie Nieuwe ontwikkelingen met Chinese satellieten in het afgelopen decennium
Nieuwe ontwikkelingen met Chinese satellieten in het afgelopen decennium Liefhebbers van het paradijselijke strand van Toscane hebben de fabriek te danken
Liefhebbers van het paradijselijke strand van Toscane hebben de fabriek te danken Russische wetenschappers leren echografie kankercellen te vinden en te doden
Russische wetenschappers leren echografie kankercellen te vinden en te doden NASA-nachtbeeld toont orkaan Paulettes met grote ogen naderen Bermuda
NASA-nachtbeeld toont orkaan Paulettes met grote ogen naderen Bermuda Digitaliseren en repliceren van de wereld van materialen
Digitaliseren en repliceren van de wereld van materialen Wat vindt het publiek van verantwoord ondernemen?
Wat vindt het publiek van verantwoord ondernemen?
- Elektronica
- Biologie
- Zonsverduistering
- Wiskunde
- French | Italian | Spanish | Portuguese | Swedish | German | Dutch | Danish | Norway |

-
Wetenschap © https://nl.scienceaq.com