
Wetenschap
draaikolk, de sleutel tot informatieverwerkingscapaciteit:Virtueel fysiek reservoir computing

Krediet:CC0 Publiek Domein
In recente jaren, fysieke reservoirberekening, een van de nieuwe informatieverwerkingstechnologieën, heeft veel aandacht getrokken. Dit is een fysieke implementatieversie van reservoir computing, dat is een leermethode die is afgeleid van de theorie van het terugkerende neuraal netwerk (RNN). Het implementeert berekeningen door het fysieke systeem te beschouwen als een enorme RNN, het uitbesteden van de belangrijkste operaties aan de dynamiek van het fysieke systeem dat het fysieke reservoir vormt. Het heeft het voordeel dat er onmiddellijk optimalisatie wordt verkregen met beperkte rekenbronnen door lineaire en statische uitleeswegingen aan te passen tussen de uitvoer en een fysiek reservoir zonder dat optimalisatie van de wegingen door terugpropagatie vereist is.
Echter, aangezien de informatieverwerkingscapaciteit afhankelijk is van de fysieke reservoircapaciteit, het is belangrijk dat dit wordt onderzocht en geoptimaliseerd. Verder, bij het ontwerpen van een fysiek reservoir met een hoog informatieverwerkingsvermogen, verwacht wordt dat de experimentele kosten zullen worden verminderd door numerieke simulatie. Bekende voorbeelden van het berekenen van fysieke reservoirs zijn de toepassing ervan op zachte materialen, fotonica, spintronica, en quanta, terwijl de afgelopen jaren veel aandacht is besteed aan golven; neuromorfe apparaten die functies van de hersenen simuleren met behulp van niet-lineaire golven zijn voorgesteld.
De vloeiende stroom van water, lucht, enz. vertegenwoordigt een fysiek systeem dat bekend is, maar verschillende en gecompliceerde patronen vertoont waarvan werd gedacht dat ze een hoog informatieverwerkingsvermogen hebben. Echter, virtueel fysiek reservoirberekening met behulp van numerieke simulatie of onderzoek naar informatieverwerkingscapaciteit van vloeistofstromingsverschijnselen is niet gerealiseerd vanwege de relatief hoge numerieke rekenkosten. Daarom, de relatie tussen de stroomvortex en informatieverwerkingscapaciteit bleef onbekend.
In dit onderzoek, Prof. Hirofumi Notsu en een afgestudeerde student van Kanazawa University in samenwerking met Prof. Kohei Nakajima van de Universiteit van Tokyo onderzochten vloeistofstromingsverschijnselen als een fysiek systeem, vooral de vloeistofstroom die rond een cilinder plaatsvindt, wat goed begrepen wordt. Het is bekend dat dit fysieke systeem wordt bepaald door de onsamendrukbare Navier-Stokes-vergelijkingen, die de vloeistofstroom beschrijven, en bevat ook het Reynoldsgetal, een parameter die indicatief is voor de systeemkenmerken.
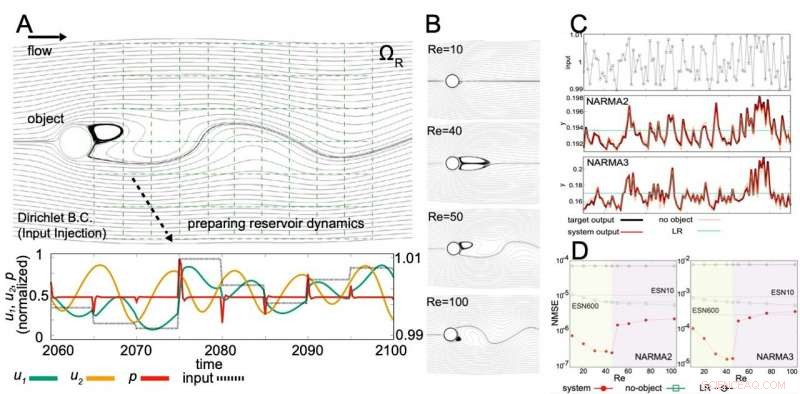
A:Overzicht van het onderzoek. B:Typische vloeistofstroom bij elk Reynolds-getal. C:Invoer langs tijdreeks en de resultaten van NARMA2- en NARMA3-modellen. Streefwaarden zijn in het zwart, terwijl de waarden van virtuele fysieke reservoirberekeningen met behulp van wervels in het rood zijn. D:Waarden van fouten (genormaliseerde gemiddelde kwadratische fouten, NMSE) op elk Reynolds-nummer in NARMA2- en NARMA3-modellen. De fout is minimaal met een Reynolds-getal rond de 40. Credit:Kanazawa University
Dit fysieke systeem werd virtueel geïmplementeerd door ruimtelijke tweedimensionale numerieke simulatie met behulp van de gestabiliseerde Lagrange-Galerkin-methode, en de dynamiek van stroomsnelheid en druk op de geselecteerde punten in het stroomafwaartse gebied van de cilinder werden gebruikt als het fysieke reservoir. De informatieverwerkingscapaciteit werd geëvalueerd met behulp van het NARMA-model.
Het is bekend dat in de vloeistofstroom rond een cilinder, naarmate de waarde van het Reynoldsgetal toeneemt, dubbele wervelingen gevormd in het stroomafwaartse gebied van de cilinder worden geleidelijk groter en vormen uiteindelijk een Karman vortexstraat, het afwisselend afstoten van wervels. In dit onderzoek, er werd verduidelijkt dat bij het Reynoldsgetal waar de dubbele wervelingen maximaal zijn, maar net voor de overgang naar een Karman vortexstraat, de informatieverwerkingscapaciteit is het hoogst.
Met andere woorden, voor de overgang naar een Karman vortex straat, de informatieverwerkingscapaciteit neemt toe naarmate de grootte van de tweelingwervels toeneemt. Anderzijds, aangezien de eigenschap echotoestand die de reproduceerbaarheid van de reservoirberekening garandeert niet kan worden gehandhaafd wanneer de overgang naar de Karman-vortexstraat plaatsvindt, het wordt duidelijk dat de Karman vortexstraat niet kan worden gebruikt voor computers.
Verwacht wordt dat deze bevindingen met betrekking tot wervelingen van vloeistofstromen en informatieverwerkingscapaciteit nuttig zullen zijn wanneer, in de toekomst, de informatieverwerkingscapaciteit van het fysieke reservoir kan worden uitgebreid met behulp van vloeistofstroom, bijv. in de ontwikkeling van op golven gebaseerde neuromorfe apparaten die onlangs zijn gerapporteerd. Hoewel de numerieke rekenkosten van fluïdumstromingsverschijnselen relatief hoog zijn, deze studie heeft het mogelijk gemaakt om macroscopische wervelingen te hanteren die fysiek gemakkelijk te begrijpen zijn en heeft de relatie tussen wervels en informatieverwerkingsmogelijkheden verduidelijkt door het virtueel implementeren van fysieke reservoirberekening met ruimtelijke tweedimensionale numerieke simulatie.
Virtuele fysieke reservoir computing, die vroeger werd toegepast op een relatief groot aantal fysieke systemen die werden beschreven als eendimensionale systemen, is uitgebreid met fysieke systemen met twee of meer ruimtelijke dimensies. Verwacht wordt dat de resultaten van dit onderzoek het mogelijk zullen maken om de informatieverwerkingscapaciteiten van een breder scala aan fysieke systemen virtueel te onderzoeken. In aanvulling, aangezien is gebleken dat draaikolken de sleutel zijn tot informatieverwerking, de verwachting is dat onderzoek naar het creëren of in stand houden van wervels verder zal worden bevorderd.
 Het verrassingselement
Het verrassingselement Hoe bereken ik de hoeveelheid zuur om de water-pH te verlagen?
Hoe bereken ik de hoeveelheid zuur om de water-pH te verlagen?  Het roosteren van cacaobonen kan zowel de gezondheidsvoordelen van chocolade behouden, smaak
Het roosteren van cacaobonen kan zowel de gezondheidsvoordelen van chocolade behouden, smaak Unieke structurele fluctuaties aan het ijsoppervlak bevorderen auto-ionisatie van watermoleculen
Unieke structurele fluctuaties aan het ijsoppervlak bevorderen auto-ionisatie van watermoleculen Onderzoekers verbeteren de synthese van bismutwolframaat met een milieuvriendelijke procedure
Onderzoekers verbeteren de synthese van bismutwolframaat met een milieuvriendelijke procedure
Hoofdlijnen
- Wat zijn de verschillen tussen een oog van een koe en een menselijk oog?
- Geheugenverlies en hoofdtrauma
- Nieuw raamwerk om microbiële interacties af te leiden
- Bodembedekkers verhogen de vernietiging van onkruidzaden in velden, licht werpen op interacties met roofdieren
- Kennis van larvale vissen slechts een druppel op de gloeiende plaat
- Vertrouwen op GPS voorkomt dat delen van uw hersenen worden geactiveerd
- Drie artikelen helpen de code van co-enzym Q-biosynthese te kraken
- Zeeschildpadden sterven nadat ze verstrikt zijn geraakt in plastic afval
- Ecologische successie: definitie, types, stadia en voorbeelden
- Onzichtbare tags:natuurkundigen schrijven, lezen en wissen met licht

- Sommige zwarte gaten wissen je verleden uit

- Experimenteel bewijs voor Zeeman spin-baankoppeling in antiferromagnetische

- Hoe maak je een eenvoudige afstandsbediening Car

- Stabiele fauteuilachtige hexazinaatring in wolfraamhexanitride
 Satellietontwerp toegepast op superjacht
Satellietontwerp toegepast op superjacht Waarom mensen in Afrika tijdens de laatste ijstijd naar de bergen vluchtten
Waarom mensen in Afrika tijdens de laatste ijstijd naar de bergen vluchtten Hoe offshore boren werkt
Hoe offshore boren werkt  Kurkentrekkerlasers gebruiken om chirale moleculen te scheiden
Kurkentrekkerlasers gebruiken om chirale moleculen te scheiden Nieuwe bio-geïnspireerde hydrogels kunnen werken als superlijm in zeer ionische omgevingen zoals zeewater
Nieuwe bio-geïnspireerde hydrogels kunnen werken als superlijm in zeer ionische omgevingen zoals zeewater De twee ontmoeten elkaar eindelijk:nanodraden en nanobuisjes gecombineerd om intracellulaire bio-elektronische sondes te vormen
De twee ontmoeten elkaar eindelijk:nanodraden en nanobuisjes gecombineerd om intracellulaire bio-elektronische sondes te vormen Maleisië redt 140 schubdieren van vermoedelijke smokkelaars
Maleisië redt 140 schubdieren van vermoedelijke smokkelaars Universele wet van aanraking zal nieuwe ontwikkelingen in virtual reality mogelijk maken
Universele wet van aanraking zal nieuwe ontwikkelingen in virtual reality mogelijk maken
- Elektronica
- Biologie
- Zonsverduistering
- Wiskunde
- Italian | Spanish | Portuguese | Swedish | German | Dutch | Danish | Norway | French |

-
Wetenschap © https://nl.scienceaq.com

