
Wetenschap
Quantum Hall-effect gereïncarneerd in 3D-topologische materialen
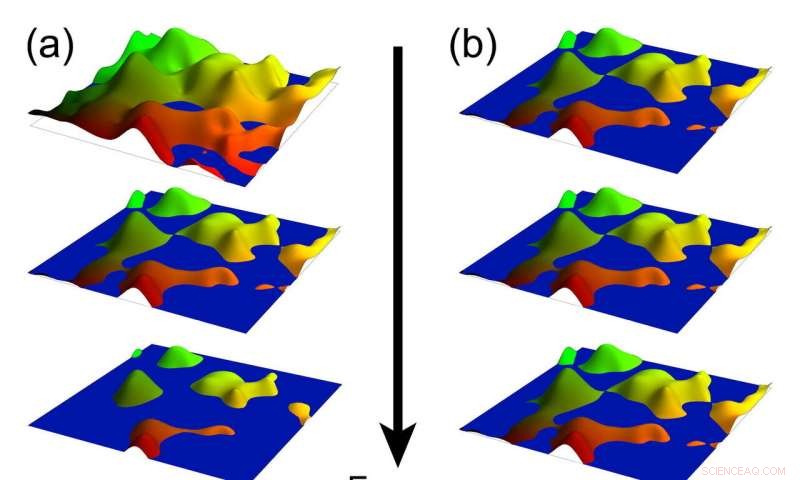
De ruige landschappen in deze illustraties verbeelden het elektrische potentieel op het oppervlak van 2D-materialen die het quantum Hall-effect vertonen. Het niveau van robuustheid komt overeen met onzuiverheden in het systeem, en het waterniveau vertegenwoordigt de "Fermi-energie, ” of vulniveau van elektronen. In het kwantum Hall-effect (links), de percolatiedrempel (midden) is een nauwkeurig afgestemde energietoestand die de overgang naar topologische orde markeert. Nieuw onderzoek door natuurkundigen van Rice University, de University of California Berkeley en het Karlsruhe Institute of Technology hebben "stapels" van deze speciale 2D-toestand gevonden die patronen van kwantumverstrengeling (rechts) beschermen door het hele oppervlakte-energiespectrum van 3D-topologische materialen. Krediet:M. Foster/Rice University
Amerikaanse en Duitse natuurkundigen hebben verrassend bewijs gevonden dat een van de beroemdste fenomenen in de moderne natuurkunde - het kwantum Hall-effect - wordt 'gereïncarneerd' in topologische supergeleiders die kunnen worden gebruikt om fouttolerante kwantumcomputers te bouwen.
De ontdekking van het kwantum Hall-effect in 1980 was het begin van de studie van topologische orden, elektronische toestanden met "beschermde" patronen van lange-afstands kwantumverstrengeling die opmerkelijk robuust zijn. De stabiliteit van deze beschermde toestanden is buitengewoon aantrekkelijk voor quantum computing, die kwantumverstrengeling gebruikt om informatie op te slaan en te verwerken.
In een studie die deze maand online is gepubliceerd in Fysieke beoordeling X ( PRX ), theoretische natuurkundigen van Rice University, de Universiteit van Californië, Berkeley (UC Berkeley), en het Karlsruhe Institute of Technology (KIT) in Karlsruhe, Duitsland, presenteerde sterk numeriek bewijs voor een verrassend verband tussen 2D- en 3D-fasen van topologische materie. Het quantum Hall-effect werd ontdekt in 2D-materialen, en laboratoria over de hele wereld zijn in een race om 3D-topologische supergeleiders voor kwantumcomputers te maken.
"In dit werk hebben we aangetoond dat een bepaalde klasse van 3D-topologische supergeleiders 'energiestapels' van 2-D elektronische toestanden aan hun oppervlak zou moeten vertonen, " zei Rice co-auteur Matthew Foster, een universitair hoofddocent natuurkunde en sterrenkunde en lid van het Rice Center for Quantum Materials (RCQM). "Elk van deze gestapelde toestanden is een robuuste 'reïncarnatie' van een enkele, zeer speciale toestand die optreedt in het 2D-quantum Hall-effect."
Het quantum Hall-effect werd voor het eerst gemeten in tweedimensionale materialen. Foster gebruikt een "percolatie" -analogie om de vreemde overeenkomsten te visualiseren tussen wat er gebeurt in 2D-quantum Hall-experimenten en de 3D-computermodellen van het onderzoek.
"Stel je een vel papier voor met een kaart van ruige pieken en dalen, en stel je dan voor wat er gebeurt als je dat landschap met water vult, "zei hij. "Het water is onze elektronen, en wanneer het vloeistofniveau laag is, je hebt gewoon geïsoleerde meren van elektronen. De meren zijn van elkaar gescheiden, en de elektronen kunnen de massa niet geleiden. Als het waterpeil hoog is, je hebt geïsoleerde eilanden, en in dit geval zijn de eilanden als de elektronen, en je krijgt ook geen bulkgeleiding."
In de analogie van Foster is het ruige landschap het elektrische potentieel van het 2D-materiaal, en het niveau van robuustheid komt overeen met de hoeveelheid onzuiverheden in het systeem. Het waterniveau vertegenwoordigt de "Fermi-energie, een begrip in de natuurkunde dat verwijst naar het vulniveau van elektronen in een systeem. De randen van de papieren kaart zijn analoog aan de 1D-randen die het 2D-materiaal omringen.
"Als je water toevoegt en het vloeistofniveau precies afstemt op het punt waar je kleine waterbruggetjes hebt die de meren met elkaar verbinden en kleine landbruggetjes die de eilanden met elkaar verbinden, dan is het net zo gemakkelijk om over het water of over land te reizen, ' zei Foster. 'Dat is de percolatiedrempel, wat overeenkomt met de overgang tussen topologische toestanden in quantum Hall. Dit is de speciale 2D-toestand in Quantum Hall.
"Als je het vloeistofpeil meer verhoogt, nu zitten de elektronen gevangen in geïsoleerde eilanden, en je zou denken, 'We zullen, Ik heb dezelfde situatie als voorheen, zonder geleiding.' Maar, bij de bijzondere overgang, een van de elektronische toestanden is tot aan de rand afgepeld. Door meer vloeistof toe te voegen, wordt de randstatus niet verwijderd, die rond het hele monster kan gaan, en niets kan het stoppen."
De analogie beschrijft de relatie tussen robuuste edge conduction en bulk fine-tuning door de speciale overgang in het quantum Hall-effect. In de PRX-studie Foster en co-auteurs Björn Sbierski van UC Berkeley en Jonas Karcher van KIT bestudeerden 3D-topologische systemen die vergelijkbaar zijn met de 2D-landschappen in de analogie.
"De interessante dingen in deze 3D-systemen gebeuren ook alleen aan de grens, " zei Foster. "Maar nu zijn onze grenzen geen 1D-randtoestanden, het zijn 2D-oppervlakken."
Met behulp van "brute-force numerieke berekeningen van de oppervlaktetoestanden, "Sbierski, Karcher en Foster vonden een verband tussen de kritische 2D-quantum Hall-toestand en de 3D-systemen. Zoals de 1D-randtoestand die blijft bestaan boven de overgangsenergie in 2D-quantum Hall-materialen, de berekeningen onthulden een persistente 2D-grenstoestand in de 3D-systemen. En niet zomaar een 2-D staat; het is precies dezelfde 2D-percolatietoestand die aanleiding geeft tot 1D quantum Hall-randtoestanden.
"Wat een verfijnde topologische kwantumfase-overgang in 2D was, is 'gereïncarneerd' als de generieke oppervlaktetoestand voor een hogere dimensionale bulk, " zei Foster. "In de studie van 2018, mijn fractie identificeerde een analoge verbinding tussen een andere, meer exotisch type 2D-kwantum Hall-effect en de oppervlaktetoestanden van een andere klasse van 3D-topologische supergeleiders. Met dit nieuwe bewijs, we zijn er nu zeker van dat er een diepe topologische reden is voor deze verbindingen, maar op dit moment blijft de wiskunde duister."
Topologische supergeleiders moeten nog experimenteel worden gerealiseerd, maar natuurkundigen proberen ze te creëren door onzuiverheden toe te voegen aan topologische isolatoren. Dit proces, bekend als doping, is op grote schaal gebruikt om andere soorten onconventionele supergeleiders te maken van bulkisolatoren.
"We hebben nu bewijs dat drie van de vijf 3D-topologische fasen zijn gekoppeld aan 2D-fasen die versies zijn van het kwantum Hall-effect, en alle drie de 3D-fasen zouden kunnen worden gerealiseerd in 'topologische supergeleiders, ' zei Foster.
Foster zei dat de conventionele wijsheid in de fysica van de gecondenseerde materie was dat topologische supergeleiders elk slechts één beschermde 2D-oppervlaktetoestand zouden bevatten en dat alle andere toestanden nadelig zouden worden beïnvloed door onvermijdelijke onvolkomenheden in de vastestofmaterialen die worden gebruikt om de supergeleiders te maken.
Maar Sbierski, De berekeningen van Karcher en Foster suggereren dat dit niet het geval is.
"In de kwantumzaal, je kunt overal afstemmen en toch dit robuuste plateau in geleiding krijgen, vanwege de 1D-randtoestanden, " zei Foster. "Ons werk suggereert dat dit ook het geval is in 3D. We zien stapels kritieke toestanden op verschillende energieniveaus, en ze worden allemaal beschermd door deze vreemde reïncarnatie van de 2-D quantum Hall-overgangstoestand."
De auteurs hebben ook de weg geëffend voor experimenteel werk om hun bevindingen te verifiëren, details uitwerken van hoe de oppervlaktetoestanden van de 3D-fasen in verschillende experimentele sondes zouden moeten verschijnen.
"We bieden nauwkeurige statistische 'vingerafdrukken' voor de oppervlaktetoestanden van de topologische fasen, Foster zei. "De eigenlijke golffuncties zijn willekeurig, wegens wanorde, maar hun distributies zijn universeel en komen overeen met de quantum Hall-overgang."
 Hoe maak je een Dendrogram
Hoe maak je een Dendrogram Broeikasgassen uit olie en gas zullen naar verwachting blijven toenemen
Broeikasgassen uit olie en gas zullen naar verwachting blijven toenemen GeoSEA-array registreert glijden van de zuidoostelijke flank van de Etna
GeoSEA-array registreert glijden van de zuidoostelijke flank van de Etna Wat is de Equators Latitude?
Wat is de Equators Latitude?
Een standaard geografisch coördinatensysteem is uitgevonden om het navigeren over de hele wereld eenvoudiger te maken. Horizontale breedtelijnen en verticale lengtelijnen vormen dit rastersysteem en verdelen de aarde in
 NASA vindt ex-tropische cycloon Uesis-regens die Nieuw-Zeeland treffen
NASA vindt ex-tropische cycloon Uesis-regens die Nieuw-Zeeland treffen
Hoofdlijnen
- Waar bestaat het cytoplasma uit?
- Drie artikelen helpen de code van co-enzym Q-biosynthese te kraken
- Componenten van Homeostasis
- Wat is vergelijkende biochemie?
- Hoe geel en blauw groen maken bij papegaaien
- De toekomst zaaien? Ark conserven zeldzaam, bedreigde planten
- Hoe bacteriën worden gereproduceerd?
- Ontdekt? Nieuw maar uitgestorven menselijk familielid uit Melanesië
- Het verschil tussen histon en nonhistone
- Naar een continue atoomlaser

- Nieuwe weg voor de grootschalige synthese van Janus-deeltjes
- Studie vergelijkt drie top-atoomklokken met recordnauwkeurigheid over zowel glasvezel als lucht

- Zwaartekrachtgolven kunnen het bestaan van het quark-gluonplasma bewijzen

- Van fotosynthese tot nieuwe verbindingen voor oogziekten

 Een platform om fluorescent gelabelde eiwitten te bereiden en hun natuurlijke omgeving te simuleren
Een platform om fluorescent gelabelde eiwitten te bereiden en hun natuurlijke omgeving te simuleren Gemeenschappen met lage inkomens voorbereiden op orkanen begint met outreach
Gemeenschappen met lage inkomens voorbereiden op orkanen begint met outreach 50 jaar na Concorde, Amerikaanse start-up kijkt naar supersonische toekomst
50 jaar na Concorde, Amerikaanse start-up kijkt naar supersonische toekomst De achteruitgang van het Caribische koraalrif begon in de jaren vijftig en zestig door lokale menselijke activiteiten
De achteruitgang van het Caribische koraalrif begon in de jaren vijftig en zestig door lokale menselijke activiteiten Elektrisch afstembare meta-oppervlakken effenen de weg naar dynamische hologrammen
Elektrisch afstembare meta-oppervlakken effenen de weg naar dynamische hologrammen Aalto-1-satelliet verzendt eerste beeld
Aalto-1-satelliet verzendt eerste beeld Hoe ESD-matten te testen
Hoe ESD-matten te testen  Vroege Cambrische ontdekking van fossielen geeft nieuw inzicht in de oorsprong van hemichordaten
Vroege Cambrische ontdekking van fossielen geeft nieuw inzicht in de oorsprong van hemichordaten
- Elektronica
- Biologie
- Zonsverduistering
- Wiskunde
- Italian | Spanish | Portuguese | Swedish | German | Dutch | Danish | Norway | French |

-
Wetenschap © https://nl.scienceaq.com

