
Wetenschap
Twijfelachtige stabiliteit van dissipatieve topologische modellen voor klassieke en kwantumsystemen

Krediet:CC0 Publiek Domein
Energiebesparing vormt de kern van elke natuurkundige theorie. Effectieve wiskundige modellen kunnen echter energiewinst en/of -verlies bevatten en daarmee de wet van behoud van energie overtreden door alleen de fysica van een subsysteem vast te leggen. Als resultaat, de Hamiltoniaan, de functie die de energie van het systeem beschrijft, verliest een belangrijke wiskundige eigenschap:het is niet langer Hermitisch. Dergelijke niet-Hermitische Hamiltonianen hebben met succes experimentele opstellingen beschreven voor zowel klassieke problemen - in b.v. sommige optische systemen en elektrische circuits - en kwantumsystemen, bij het modelleren van de beweging van elektronen in kristallijne vaste stoffen. In een nieuwe krant in EPJ D , natuurkundigen Rebekka Koch van de Universiteit van Amsterdam in Nederland en Jan Carl Budich van de Technische Universität Dresden, in Duitsland, beschrijven hoe deze functies nieuwe inzichten verschaffen in gedrag aan de randen van topologische materialen.
Echter, niet-Hermitiaanse Hamiltonianen breken met concepten die bekend zijn van energiebesparende systemen zoals de bulk-boundary correspondentie (BBC) in deze materialen. Deze overeenkomst relateert de topologische eigenschappen van het grootste deel van het materiaal aan de fysica van de randen. In het Hermitische geval het grootste deel van zo'n materiaal kan worden beschreven door de randen te verwaarlozen en gewoon aan te nemen dat het materiaal oneindig of periodiek is, omdat grenseffecten de fysica van de binnenkant niet beïnvloeden.
Verrassend genoeg, dit geldt niet meer als de energie niet behouden blijft:de eigenschappen van de begrenzing hebben ineens een enorme invloed op het bulksysteem en daar moet vervolgens rekening mee worden gehouden. Het leidt tot een drastisch gewijzigde BBC (bulk-boundary correspondentie) voor niet-Hermitische systemen. Vooral, Koch en Budich bestudeerden verschillende sterktes van de koppeling tussen grenzen en hun effect op het bulksysteem. Wetende dat er in realistische kwantummechanische systemen altijd een interactie is tussen de randen - weliswaar een extreem kleine - onderzochten ze in hoeverre ontkoppelde randen over het algemeen waarneembaar zijn. Koch en Budich ontdekten dat het spectrum van het topologische materiaal stabiel is onder fysiek gemotiveerde verstoringen zoals de onderdrukte interacties tussen de grenzen.
Hoofdlijnen
- Nieuwe genen op verslechterend Y-chromosoom
- Race om Indonesische krokodil te redden die is getroffen door een bandenketting
- Verschillen en overeenkomsten tussen Unicellular & Cellular
- Hoe is de taal geëvolueerd?
- DNA-onderzoekers roepen botverzamelaars op om toegang tot botten te delen
- Is lachen besmettelijk?
- Bijvangst verantwoordelijk voor achteruitgang Nieuw-Zeelandse zeeleeuw
- Hoe reproduceren algen zich?
- Probiotica (vriendelijke bacteriën): wat is het en hoe helpt het ons?
- Nieuwe roadmap naar beter presterende zonne-energiecellen
- Lasergestuurde techniek voor het creëren van fusie is nu binnen handbereik, zeggen onderzoekers

- Cesiumdamp helpt bij het zoeken naar donkere materie

- Er is geen manier om de lichtsnelheid in één richting te meten

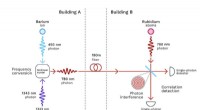
- Wetenschappers correleren fotonparen van verschillende kleuren die in afzonderlijke gebouwen zijn gegenereerd
 Een atoomchip-interferometer die kwantumzwaartekracht kan detecteren
Een atoomchip-interferometer die kwantumzwaartekracht kan detecteren Wetenschappers synthetiseren loodvrije op zirkonium gebaseerde vacature-geordende dubbele perovskiet nanokristallen
Wetenschappers synthetiseren loodvrije op zirkonium gebaseerde vacature-geordende dubbele perovskiet nanokristallen Vrouwen in de wetenschap stellen minder vragen dan mannen, volgens nieuw onderzoek
Vrouwen in de wetenschap stellen minder vragen dan mannen, volgens nieuw onderzoek Besluitvorming van vijf nanoseconden:nieuw chipontwerp om onderzoekers snel te kunnen rekenen
Besluitvorming van vijf nanoseconden:nieuw chipontwerp om onderzoekers snel te kunnen rekenen Apple tegen wetgevers:Siri luistert niet totdat daarom wordt gevraagd
Apple tegen wetgevers:Siri luistert niet totdat daarom wordt gevraagd Gewelddadige misdaad is als een besmettelijke ziekte - en we weten hoe we de verspreiding ervan kunnen stoppen
Gewelddadige misdaad is als een besmettelijke ziekte - en we weten hoe we de verspreiding ervan kunnen stoppen Tikken geheimen van Aussie spiders unieke zijde
Tikken geheimen van Aussie spiders unieke zijde Kan niet typen? Apple staat voor class action-rechtszaak wegens defecte MacBook-toetsenborden
Kan niet typen? Apple staat voor class action-rechtszaak wegens defecte MacBook-toetsenborden
- Elektronica
- Biologie
- Zonsverduistering
- Wiskunde
- French | Italian | Spanish | Portuguese | Swedish | German | Dutch | Danish | Norway |

-
Wetenschap © https://nl.scienceaq.com


