Wetenschap
Wetenschappers voorkomen kritieke ineenstorting van solitonen van hogere orde
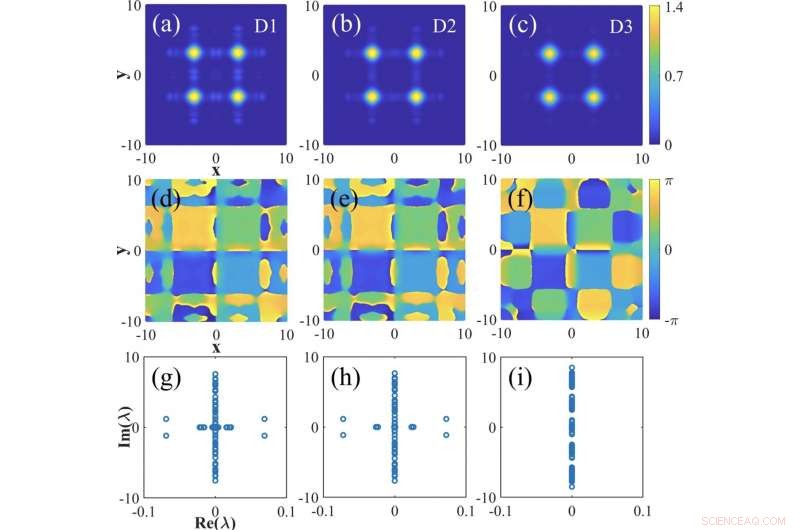
contourplots, fasen, en eigenwaarden van vortex gap solitons verschijnen als quadruple-mode gebonden toestanden. Krediet:XIOPM
Solitonen zijn stabiele objecten die in evenwicht worden gehouden door diffractie of dispersie en niet-lineariteit. Een fundamentele uitdaging op dit gebied is de stabilisatie van solitonen in multidimensionale coördinaten, aangezien de 2-D en 3-D solitonen in de vrije ruimte altijd onstabiel zijn en respectievelijk kritische ineenstortingen ondergaan als gevolg van catastrofale zelffocusserende niet-lineariteit.
De stabilisatie van multidimensionale gelokaliseerde toestanden is meestal afhankelijk van lineaire periodieke media met uniforme niet-lineariteit. Hoewel niet-lineaire roosters met vloeiende variatie van niet-lineariteit verschillende soorten solitonen kunnen ondersteunen. Echter, bestaan en stabiliteitseigenschappen van solitonen met kubieke-quintische niet-lineariteiten en 2-D lineair periodiek potentieel moeten nog worden onthuld. Is er een model of methode om kritieke ineenstorting van solitonen van hogere orde te voorkomen?
Een onderzoeksteam onder leiding van Prof. Dr. Zeng Jianhua van het Xi'an Institute of Optics and Precision Mechanics (XIOPM) van de Chinese Academie van Wetenschappen (CAS) stelt een haalbaar schema voor om 2-D gelokaliseerde modi te stabiliseren tegen kritieke ineenstorting door rekening te houden met de fractionele diffractievolgorde naar lichtvoortplanting in periodieke fysieke systemen met concurrerende zelffocusserende en zelf-defocusserende niet-lineariteiten in kubieke-kwanttische niet-lineaire termen. Het resultaat is gepubliceerd in Communicatie Fysica .
Ze stellen theoretisch een raamwerk voor van 2-D niet-lineaire fractionele Schrödingervergelijking (NLFSE), die de kritieke ineenstorting kan onderdrukken. Ze onthullen dat het model een verscheidenheid aan stabiele solitonfamilies produceert, inclusief 2-D fundamentele gap en verticale solitonen evenals gap soliton clusters (solitonen zijn altijd onstabiel in het quintic-only model).
Een gedetailleerd inzicht in de dynamische eigenschappen van solitonen laat verder zien dat de solitonen robuust stabiel zijn in het midden van de bandgaps van het onderliggende lineaire Bloch-spectrum, terwijl onstabiel nabij de randen van de bandhiaten; en de stabiliteit van de solitonen wordt matig beïnvloed door niet-lineaire sterkte.
De opmerkelijke ontdekking biedt een nieuwe weg om het bestaan en de dynamische eigenschappen van 2-D gelokaliseerde modi te onderzoeken door de diffractievolgorde en afstembare bandhiaten van de periodieke fysieke systemen te beheren.
 Onderzoek maakt oplaadbare batterijen met een langere levensduur mogelijk
Onderzoek maakt oplaadbare batterijen met een langere levensduur mogelijk Wetenschappers zetten giftige pesticiden om in behandeling tegen antibioticaresistente bacteriën
Wetenschappers zetten giftige pesticiden om in behandeling tegen antibioticaresistente bacteriën Onderzoek brengt vroege ziekteverschijnselen in de schijnwerpers met infraroodlicht
Onderzoek brengt vroege ziekteverschijnselen in de schijnwerpers met infraroodlicht Concentreer je een oplossing
Concentreer je een oplossing Spierachtig materiaal zet uit en trekt samen als reactie op licht
Spierachtig materiaal zet uit en trekt samen als reactie op licht
 Uit onderzoek blijkt dat aardbevingen nog jaren doorgaan nadat de injectie van afvalwater in het gasveld is gestopt
Uit onderzoek blijkt dat aardbevingen nog jaren doorgaan nadat de injectie van afvalwater in het gasveld is gestopt Symbiotische gigantische bacteriën stellen doktersvissen in de Rode Zee in staat hun dieet te specialiseren
Symbiotische gigantische bacteriën stellen doktersvissen in de Rode Zee in staat hun dieet te specialiseren Wanneer een stip een storm beïnvloedt
Wanneer een stip een storm beïnvloedt Hoe een afvalwaterzuiveringsinstallatie te maken Model
Hoe een afvalwaterzuiveringsinstallatie te maken Model Vier keer giftiger:hoe natuurbrandrook in de loop van de tijd veroudert
Vier keer giftiger:hoe natuurbrandrook in de loop van de tijd veroudert
Hoofdlijnen
- De juiste manier om DNA te repareren
- De zeeschildpad die weigerde te worden geslagen door de storm
- Nieuwe online database brengt het genoom in beeld met behulp van moleculaire structuur
- Wat zou er gebeuren als een cel geen ribosomen had?
Cellen zijn de kleinste functionele eenheden van alle levende wezens. In de cellen bevinden zich gespecialiseerde structuren, organellen genaamd, die ze helpen bepaalde functies uit te voeren. Rib
- Wat zijn de stappen van de stikstofcyclus?
- Wat gebeurt er met een Zygote na de bevruchting?
- Zullen we binnenkort uitgestorven zijn?
- Onderzoek Topic Ideeën voor Biologie
- Wat is een eigenschap die het resultaat is van twee dominante genen?
 Embraer duikt met verlies 2e kwartaal
Embraer duikt met verlies 2e kwartaal Nieuwe aanpak voor moderne elektriciteitsnetten die de efficiëntie verhoogt, verlaagt de kosten
Nieuwe aanpak voor moderne elektriciteitsnetten die de efficiëntie verhoogt, verlaagt de kosten Milieuvriendelijke nanodeeltjes voor kunstmatige fotosynthese
Milieuvriendelijke nanodeeltjes voor kunstmatige fotosynthese De theorie dat mensen in Afrika zijn ontstaan, wordt vaak in twijfel getrokken - dat is goed voor de wetenschap
De theorie dat mensen in Afrika zijn ontstaan, wordt vaak in twijfel getrokken - dat is goed voor de wetenschap Hoe Bushnell Telescopen te gebruiken
Hoe Bushnell Telescopen te gebruiken 14 staten klagen aan dat de VS de smogregels niet hebben nageleefd
14 staten klagen aan dat de VS de smogregels niet hebben nageleefd Robuuste en goedkope katalysatoren voor waterstofproductie
Robuuste en goedkope katalysatoren voor waterstofproductie Grappig bot:uit onderzoek blijkt dat 99 procent van de bètastudenten de humor van instructeurs waardeert
Grappig bot:uit onderzoek blijkt dat 99 procent van de bètastudenten de humor van instructeurs waardeert
- Elektronica
- Biologie
- Zonsverduistering
- Wiskunde
- French | Italian | Spanish | Portuguese | Swedish | German | Dutch | Danish | Norway |

-
Wetenschap © https://nl.scienceaq.com