
Wetenschap
Patronen die typisch in water worden waargenomen, zijn ook te vinden in licht

Solitongolfinteracties in ondiep water. Krediet:Liron Barakiva
Soms in ondiep water, er kan een type golf ontstaan dat veel stabieler is dan gewone golven. Solitons genoemd, deze verschijnselen ontstaan als solitaire golven en kunnen lange afstanden afleggen terwijl ze hun vorm en snelheid behouden, zelfs na aanvaring met andere golven.
Echter, in bepaalde gevallen kunnen solitonbotsingen gecompliceerde golfpatronen genereren, soms "alfabetgolven" genoemd omdat ze lijken op de letters X, ja, en H, evenals combinaties van deze vormen. Soliton-golven en hun botsingspatronen hebben wetenschappers gefascineerd sinds ze werden ontdekt in de 19 e eeuw.
Nu in een nieuwe studie, onderzoekers hebben ontdekt dat dezelfde patronen in watergolven ook ontstaan bij botsingen van optische solitonen (lichtgolven met dezelfde stabiele eigenschappen). De onderzoekers laten zien dat dezelfde vergelijking, genaamd de Kadomtsev-Petviashvili II (KPII) vergelijking, die wordt gebruikt om water-solton-interacties te modelleren, kan ook worden gebruikt om optische soliton-interacties te modelleren, het onthullen van een nauw verband tussen de golfdynamiek van water en licht.
Theodoros P. Horikis, bij de faculteit Wiskunde, Universiteit van Ioánnina, en Dimitrios J. Frantzeskakis, bij de afdeling Natuurkunde, Universiteit van Athene, hebben een artikel gepubliceerd over de patronen in optische solitonen in een recent nummer van Proceedings van de Royal Society A .
"We zijn allemaal op een strand geweest en hebben de ingewikkelde patronen opgemerkt die golven vormen in het ondiepe, nabij de kustlijn:prachtige X-, Y-, en zelfs H-vormige golfvormen komen vaak voort uit de interactie van rechte golven, " vertelde Horikis Phys.org . "Opmerkelijk, deze verschijnselen worden volledig begrepen en kunnen wiskundig in detail worden beschreven met behulp van geschikte wiskundige modellen. Oppervlaktespanning, dat is het fenomeen dat ervoor zorgt dat vloeistoffen het gebied dat ze innemen minimaliseren, speelt een belangrijke rol bij de vorming van X-, Y-, en H-vormige golven. In water, oppervlaktespanning is klein, terwijl in kwik, bijvoorbeeld, oppervlaktespanning is groot.
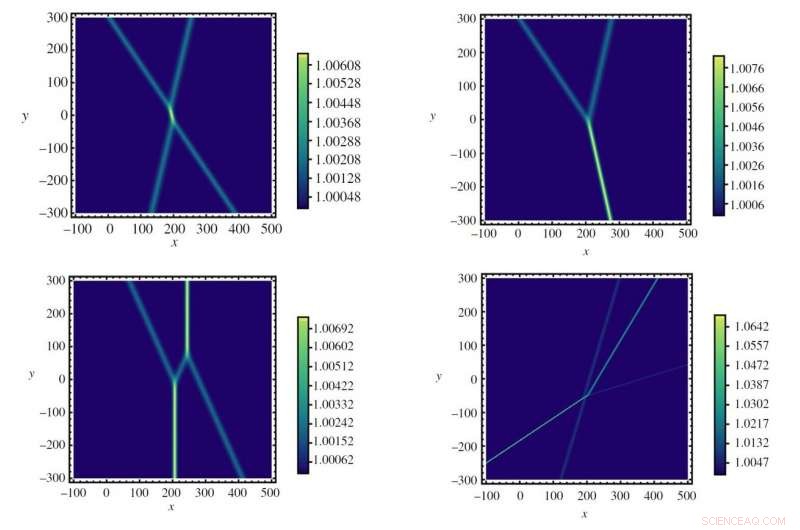
Simulatieresultaten die verschillende patronen laten zien die ontstaan in optische soliton-interacties. Krediet:Horikis en Frantzekakis. ©2019 De Koninklijke Maatschappij
"We hebben aangetoond dat optische soliton-voortplanting in niet-lokale media - waaronder plasma's, nematische vloeibare kristallen en vloeibare oplossingen met thermische niet-lineariteiten - wordt beheerst door hetzelfde model dat wordt gebruikt om ondiepe wateren te beschrijven, waarbij niet-lokaliteit de rol van oppervlaktespanning speelt. Dus, inderdaad, 'licht ontmoet water, ' zoals we voorspellen dat X-, Y-, H-vormig, en zelfs meer gecompliceerde golfstructuren die we waarnemen in vlakke stranden, kunnen ook worden waargenomen in optica, als optische bundels die zich voortplanten in niet-lokale niet-lineaire media."
Zoals de onderzoekers uitlegden, een optisch medium is niet-lokaal wanneer zijn reactie op licht niet alleen afhangt van de positie waar het externe optische veld wordt aangelegd (zoals in een lokaal medium), maar ook op het totale oppervlak en volume van het medium. In niet-lokale media, licht dat op een bepaald punt invalt, wordt afgevoerd naar de omgeving, zodat een smalle gelokaliseerde optische bundel een ruimtelijk brede respons van het medium kan induceren. De analogie tussen de zwakke oppervlaktespanning van water en de sterke niet-lokaliteit in bepaalde optische media maakt de beschrijving van optische solitonen in termen van de KPII-vergelijking mogelijk.
"Wat belangrijk is in ons artikel is dat deze twee verschijnselen, nonlocaliteit in optica en oppervlaktespanning in water, lijkt een één-op-één correspondentie te hebben, bij wijze van spreken, "zei Horikis. "Belangrijk, optische solitons die onstabiel zouden zijn in media met een zwakke niet-lokaliteit, of in vloeistoffen met een sterke oppervlaktespanning (zoals kwik), kan stabiel worden in sterk niet-lokale optische media. Vanwege dit belangrijke stabilisatie-effect dat wordt veroorzaakt door de sterke niet-lokaliteit, het optische medium van de gastheer kan solitons ondersteunen, net als het wateroppervlak, waarvan het contact met lucht werkt als een dun elastisch vel waarop deze 'alfabetgolven' zich kunnen vormen!"
Op basis van dit resultaat, de onderzoekers gebruikten numerieke simulaties om botsingen van twee of drie optische solitonen te modelleren. Net als bij de water soliton case, ze vonden dat X-, Y-, en H-vormige golven ontstonden, en ook dat de hoek van op elkaar inwerkende solitonen tot verschillende patronen leidt.
De onderzoekers verwachten dat het mogelijk is om deze optische solitonpatronen experimenteel te observeren met behulp van technologie die recentelijk is gebruikt om individuele solitonen te observeren. Dit zou het combineren van twee solitons in een niet-lokaal medium vereisen, bijvoorbeeld een nematisch vloeibaar kristal - terwijl spiegels worden gebruikt om de hoek te regelen tussen de twee lichtstralen die worden gebruikt om de solitonen te genereren.
Hun bevindingen suggereren dat het in de toekomst misschien ook mogelijk is om nog ingewikkelder patronen te vinden, zoals webachtige structuren van golven, bij botsingen van optische solitonen. Ze zijn ook van plan te onderzoeken of andere zeer niet-lokale systemen, zoals Bose-Einstein-condensaten (macroscopische kwantumsystemen samengesteld uit ultrakoude atomen) en colloïden (mengsels die deeltjes bevatten die in oplossing zijn gesuspendeerd), kan ook de nodige ingrediënten leveren om het ontstaan van deze patronen te ondersteunen.
© 2019 Wetenschap X Netwerk
 NASA vindt zware regenval van tropische storm Maha boven Lakshadweep
NASA vindt zware regenval van tropische storm Maha boven Lakshadweep Milieubewegingen, big ag verenigt u voor Amazon in Brazilië
Milieubewegingen, big ag verenigt u voor Amazon in Brazilië De stratosfeer:waar vogels en vliegtuigen vliegen en bacteriën gedijen
De stratosfeer:waar vogels en vliegtuigen vliegen en bacteriën gedijen  'S Werelds eerste dieren veroorzaakten opwarming van de aarde
'S Werelds eerste dieren veroorzaakten opwarming van de aarde Voorspellers:Droogte deze winter waarschijnlijker dan sneeuwstormen
Voorspellers:Droogte deze winter waarschijnlijker dan sneeuwstormen
Hoofdlijnen
- Welke mechanismen zorgen voor de nauwkeurigheid van DNA-replicatie?
- Over de zes koninkrijken
- Structuur van het hart Cell
- De rol van GTE in DNA-extractie
- Studie lost waarom drinken je de munchies geeft
- Interacties tussen eenvoudige moleculaire mechanismen leiden tot complexe infectiedynamiek
- Wat gebeurt er met cellen als gevolg van een natriumonbalans?
- Bloemen geheim signaal voor bijen en andere verbazingwekkende nanotechnologieën verborgen in planten
- Synthetische seks in gist belooft veiligere medicijnen voor mensen
 NASA kijkt binnen categorie 5 orkaan Maria voor en na de eerste aanlanding
NASA kijkt binnen categorie 5 orkaan Maria voor en na de eerste aanlanding Hardheid van de huid om een betere menselijke thermische status te schatten
Hardheid van de huid om een betere menselijke thermische status te schatten ESA's volgende zonnemissie zal een schaduwwerpend paar zijn
ESA's volgende zonnemissie zal een schaduwwerpend paar zijn DeepMind gebruikt neuraal netwerk om meta-leren bij mensen te helpen verklaren
DeepMind gebruikt neuraal netwerk om meta-leren bij mensen te helpen verklaren APNewsBreak:Staat onderzoekt stralingsklacht MIT-lab
APNewsBreak:Staat onderzoekt stralingsklacht MIT-lab De wet komt dichterbij op Facebook en de digitale gangsters
De wet komt dichterbij op Facebook en de digitale gangsters Autofabrikanten melden lagere autoverkopen in het eerste kwartaal van het eerste kwartaal door virushit
Autofabrikanten melden lagere autoverkopen in het eerste kwartaal van het eerste kwartaal door virushit Nanobuiskathode klopt groot, dure laser
Nanobuiskathode klopt groot, dure laser
- Elektronica
- Biologie
- Zonsverduistering
- Wiskunde
- French | Spanish | Portuguese | Swedish | German | Dutch | Danish | Norway | Italian |

-
Wetenschap © https://nl.scienceaq.com






