
Wetenschap
Huidige geluiden van Majorana-fermionen
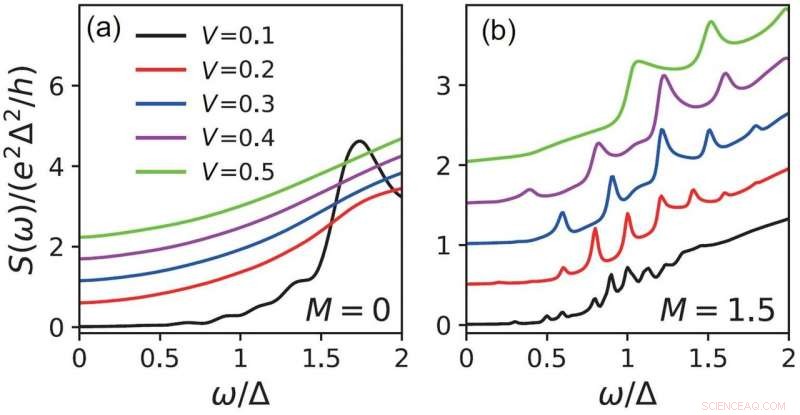
De niet-evenwichtsruis bij een eindige frequentie voor verschillende waarden van de aangelegde voorspanning voor een topologische Josephson-overgang met twee verschillende transmissiewaarschijnlijkheden D =1 (a) en D <1 (b), respectievelijk. De pieken in de rechter figuur onthullen het bestaan van de Majorana-fermionen. Krediet:©Science China Press
Majorana-fermionen zijn deeltjes die hun eigen antideeltjes zijn. In de fysica van de gecondenseerde materie, nul-energie Majorana-fermionen gehoorzamen aan niet-abelse statistieken, en kan worden gebruikt in fouttolerante topologische kwantumberekeningen. Ze zijn dan ook het onderwerp van uitgebreide studies. Echter, aangezien Majorana-fermionen geen elektrische lading dragen, het experimenteel detecteren ervan is nog steeds een uitdaging. Een huidige ruisstudie biedt nu een directe methode voor de detectie van deze nieuwe deeltjes.
De krant, getiteld "Huidige ruis in een topologische Josephson-kruising, " werd gepubliceerd in WETENSCHAP CHINA Natuurkunde, Mechanica en astronomie , wiens corresponderende auteurs Prof. Hua Jiang van Soochow University en Prof. X.C. Xie van Peking University zijn. Met behulp van de niet-evenwichtsfunctiemethode van Green, de auteurs analyseren de stroom over een topologische Josephson-junctie en gerelateerde stroomruis, het onthullen van de relatie tussen het bestaan van Majorana-fermionen en niet-evenwichtsstroomruis.
Er is voorspeld dat een topologische Josephson-junctie twee nul-energetische Majorana-gebonden toestanden kan bevatten aan de interfaces als de tijdomkeringssymmetrie wordt verbroken. Deze gebonden toestanden geven aanleiding tot twee 4π periodieke energiefaserelaties die overeenkomen met verschillende pariteiten en elkaar kruisen. Dergelijke energie-faserelaties leiden tot een fractioneel Josephson-effect van dezelfde periodiciteit. Hoe dan ook, in een realistisch systeem, de oneindig kleine energiekloof die wordt geopend door het effect van de eindige grootte, zal de 2π-periodiciteit herstellen. In niet-evenwicht, de Majorana-gebonden toestanden kunnen deze energiekloof overbruggen onder een bias V. Theoretisch werk heeft voorspeld dat de huidige ruis een piek vertoont bij ω=eV vanwege de koppeling tussen Majorana-gebonden toestanden en het continuüm. Echter, deze Majorana-gebonden toestanden kunnen ook het continuüm koppelen nadat een proces van meerdere Andreev-reflecties op de interfaces plaatsvindt, resulterend in nieuwe verschijnselen.
Gebaseerd op de niet-evenwichts-groene functiemethode, de onderzoekers bestudeerden het effect van de meervoudige Andreev-reflecties zowel in afwezigheid als in aanwezigheid van een DC-biasspanning. Ze laten zien dat de evenwichtsruis en de evenwichtsstroom dezelfde 2π-periodiciteit vertonen als die in conventionele knooppunten vanwege het effect van eindige grootte. Echter, de dips van de evenwichtsruis geven de signatuur van het fractionele Josephson-effect aan. Anderzijds, de meervoudige Andreev-reflecties veroorzaakten pieken van eindige frequentie niet-evenwichtsruis die verscheen bij ω =neV, het leveren van een bewijs voor de experimentele detectie van deze Majorana-gebonden toestanden.
 De code voor roetvorming kraken - wetenschappers ontrafelen mysterie om gevaarlijke emissies te helpen verminderen
De code voor roetvorming kraken - wetenschappers ontrafelen mysterie om gevaarlijke emissies te helpen verminderen een nieuwe, snellere manier om diblock-polymeermaterialen te verwerken
een nieuwe, snellere manier om diblock-polymeermaterialen te verwerken Commercieel gebruik van natriumpolyacrylaat
Commercieel gebruik van natriumpolyacrylaat Elektronische tong zorgt voor de snelle, goedkope detectie van vervalste honing
Elektronische tong zorgt voor de snelle, goedkope detectie van vervalste honing Nieuwe technologie zet afvalplastic in een uur om in vliegtuigbrandstof
Nieuwe technologie zet afvalplastic in een uur om in vliegtuigbrandstof
 Erosie-instabiliteiten op landschapsschaal in het noorden van Gabilan Mesa, Californië
Erosie-instabiliteiten op landschapsschaal in het noorden van Gabilan Mesa, Californië Nieuwe zuiveringstechnieken voor gezondere aquatische ecosystemen
Nieuwe zuiveringstechnieken voor gezondere aquatische ecosystemen Uit onderzoek blijkt dat de omstandigheden op het landoppervlak van invloed kunnen zijn op convectieve systemen op mesoschaal terwijl ze in beweging zijn
Uit onderzoek blijkt dat de omstandigheden op het landoppervlak van invloed kunnen zijn op convectieve systemen op mesoschaal terwijl ze in beweging zijn Nieuwe voorspellingsmodellen kunnen hittegerelateerde sterfgevallen helpen voorkomen
Nieuwe voorspellingsmodellen kunnen hittegerelateerde sterfgevallen helpen voorkomen Hoe kevers te identificeren in Ontario, Canada
Hoe kevers te identificeren in Ontario, Canada
Hoofdlijnen
- Hittetolerante broccoli voor de toekomst
- Welke soorten cellen zijn bacteriën?
- Overeenkomsten tussen huidcellen en zenuwen
- De definitie van moleculaire celbiologie
- Het bewijs zit in de voetafdruk:mensen kwamen eerder naar Amerika dan gedacht
- Wilt u 41 procent van de zeer bedreigde gewervelde planeten redden? Werken op eilanden
- Chloroplast & Mitochondria: wat zijn de overeenkomsten en verschillen?
- De functie van Peyers-patches
- Wat breekt een dubbele helix van DNA af?
- Vormgeven van terahertz-stralen met extreem hoge precisie via 3D-printen

- Schaalbare fotonische computer lost het deelverzamelingsomprobleem op

- Dichtheid van koolzuurhoudend water

- Op zoek naar onzichtbare axion donkere materie met een nieuwe meercellige haloscoop
- Experimenten met zwevende nanodeeltjes onthullen de rol van wrijving op nanoschaal

 The Signs of Weasels
The Signs of Weasels Advocatenkantoren moedigen mannen niet aan om ouderschapsverlof op te nemen
Advocatenkantoren moedigen mannen niet aan om ouderschapsverlof op te nemen Statistisch bewijs voor temperatuurinversies in ultrahete Jupiters
Statistisch bewijs voor temperatuurinversies in ultrahete Jupiters Onzekerheid over toekomstige opname van kooldioxide in Zuidelijke Oceaan gehalveerd
Onzekerheid over toekomstige opname van kooldioxide in Zuidelijke Oceaan gehalveerd Sporen van DNA blootgelegd door gedraaid licht
Sporen van DNA blootgelegd door gedraaid licht Delen van een rijstplant
Delen van een rijstplant Bosbranden kunnen op lange termijn gezondheidsproblemen veroorzaken voor bedreigde orang-oetans
Bosbranden kunnen op lange termijn gezondheidsproblemen veroorzaken voor bedreigde orang-oetans Katalysator voor de koolstofvrije productie van waterstofgas uit ammoniak
Katalysator voor de koolstofvrije productie van waterstofgas uit ammoniak
- Elektronica
- Biologie
- Zonsverduistering
- Wiskunde
- French | Spanish | Portuguese | Swedish | German | Dutch | Danish | Norway | Italian |

-
Wetenschap © https://nl.scienceaq.com

