
Wetenschap
Studie biedt een nieuwe theoretische benadering voor het beschrijven van faseovergangen die niet in evenwicht zijn
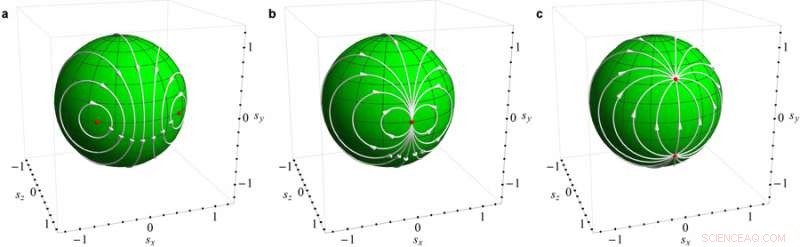
Twee natuurkundigen uit Argonne boden een manier aan om een bepaald natuurkundig fenomeen wiskundig te beschrijven, een faseovergang genaamd, in een systeem dat uit evenwicht is (dat wil zeggen, met energie die er doorheen beweegt) met behulp van denkbeeldige getallen. De illustratie relateert de faseovergang aan de verandering tussen wiskundige Mobius-transformaties (a, B, en C). De theorie van de fysica buiten evenwicht is een lang gezocht doel in het veld, en zou ons uiteindelijk kunnen helpen om betere elektronica te ontwerpen. Krediet:Vinokur/Galda/Argonne Nationaal Laboratorium
Denkbeeldige getallen zijn een oplossing voor een zeer reëel probleem in een studie die vandaag is gepubliceerd in Wetenschappelijke rapporten .
Twee natuurkundigen van het Argonne National Laboratory van het Amerikaanse ministerie van Energie boden een manier aan om een bepaald natuurkundig fenomeen wiskundig te beschrijven, de zogenaamde faseovergang in een systeem dat uit evenwicht is. Dergelijke verschijnselen staan centraal in de natuurkunde, en begrijpen hoe ze zich voordoen is een lang gekoesterd en vervelend doel geweest; hun gedrag en gerelateerde effecten zijn de sleutel tot het ontsluiten van mogelijkheden voor nieuwe elektronica en andere technologieën van de volgende generatie.
in de natuurkunde, "evenwicht" verwijst naar een toestand waarin een object niet in beweging is en er geen energie doorheen stroomt. Zoals je misschien verwacht, het grootste deel van ons leven speelt zich buiten deze staat af:we zijn constant in beweging en zorgen ervoor dat andere dingen in beweging komen.
"Een regenbui, deze draaiende ventilator, deze systemen zijn allemaal uit evenwicht, " zei studie co-auteur van de Valerii Vinokur, een Argonne Distinguished Fellow en lid van de gezamenlijke Argonne-University of Chicago Computation Institute. "Als een systeem in evenwicht is, we weten dat het altijd de laagst mogelijke energieconfiguratie heeft, maar voor niet-evenwicht werkt dit fundamentele principe niet; en ons vermogen om de fysica van dergelijke systemen te beschrijven is zeer beperkt."
Hij en co-auteur Alexey Galda, een wetenschapper bij Argonne en het James Franck Institute van de Universiteit van Chicago, had gewerkt aan manieren om deze systemen te beschrijven, vooral degenen die een faseovergang ondergaan - zoals het moment tijdens een onweersbui wanneer het ladingsverschil tussen wolk en grond te hoog toppen, en er vindt een blikseminslag plaats.
Ze vonden hun nieuwe benadering van niet-evenwichtsfysica in een nieuwe tak van de kwantummechanica. In de taal van de kwantummechanica, de energie van een systeem wordt weergegeven door wat een Hamiltoniaanse operator wordt genoemd. traditioneel, kwantummechanica had geoordeeld dat de operator om het systeem weer te geven geen denkbeeldige getallen kan bevatten als dit zou betekenen dat de energie niet als een "echte" en positieve waarde naar buiten komt - omdat het systeem in werkelijkheid echt bestaat. Deze toestand wordt Hermiticiteit genoemd.
Maar natuurkundigen hebben beter gekeken naar operators die Hermiticiteit schenden door denkbeeldige componenten te gebruiken. Vinokur zei; verschillende van dergelijke operatoren die een paar jaar geleden zijn ontdekt, worden nu veel gebruikt in de kwantumoptica.
"We hebben gemerkt dat dergelijke operators een prachtig wiskundig hulpmiddel zijn om processen die niet in evenwicht zijn te beschrijven, " hij zei.
Om de faseovergang te beschrijven, Galda en Vinokur schreven de Hamiltoniaanse operator uit, introduceerde een uitgeoefende kracht om het uit evenwicht te brengen, en toen maakten ze de kracht denkbeeldig.
"Dit is een truc die vanuit gezond verstand onwettig is, maar we zagen dat deze combinatie, energie plus denkbeeldige kracht, beschrijft perfect wiskundig de dynamiek van het systeem met wrijving, ' zei Vinokur.
Ze pasten de truc toe om andere faseovergangen buiten evenwicht te beschrijven, zoals een dynamische Mott-overgang en een spinsysteem, en zag dat de resultaten overeenkwamen met waargenomen experimenten of simulaties.
In hun laatste werk, ze verbonden hun beschrijving met een operatie die een Möbius-transformatie wordt genoemd, die voorkomt in een tak van de wiskunde die topologie wordt genoemd. "We kunnen niet-evenwichtsovergangen nu begrijpen als topologische overgangen in de ruimte van energie, ' zei Galda.
Dit stukje kwantumonheil moet dieper worden begrepen, ze zeiden, maar is toch waardevol; de theorie beschrijft basisgebieden van de natuurkunde die van groot belang zijn voor de volgende generatie elektronicatechnologie.
"Voorlopig lijkt de verbinding met topologie op wiskundige snoepjes, iets moois dat we nog niet kunnen gebruiken, maar we weten uit de geschiedenis dat als de wiskunde elegant genoeg is, al snel volgen de praktische implicaties ervan, ' zei Vinokur.
 Het produceren van ethaan uit methaan met behulp van een fotochemische lusstrategie
Het produceren van ethaan uit methaan met behulp van een fotochemische lusstrategie Hoe Redox-vergelijkingen in evenwicht te brengen
Hoe Redox-vergelijkingen in evenwicht te brengen "The R134a vs. the R410a
"The R134a vs. the R410a Wetenschappers ontdekken mogelijke methode om de bacteriën die tuberculose veroorzaken uit te hongeren
Wetenschappers ontdekken mogelijke methode om de bacteriën die tuberculose veroorzaken uit te hongeren Hondenvoer verrukkelijker maken door aroma's te analyseren
Hondenvoer verrukkelijker maken door aroma's te analyseren
 Nieuwe tornado-slachtofferanalyse zal toekomstige voorspellingen verbeteren
Nieuwe tornado-slachtofferanalyse zal toekomstige voorspellingen verbeteren Waterbesparende alternatieve voedergewassen voor Texaanse vee
Waterbesparende alternatieve voedergewassen voor Texaanse vee Parijs experimenteert met zelfrijdende bussen (update)
Parijs experimenteert met zelfrijdende bussen (update) Het belang van rode wormen in het ecosysteem
Het belang van rode wormen in het ecosysteem  De Atlantische Oceaan krijgt misschien een vliegende start vanaf de andere kant van de wereld
De Atlantische Oceaan krijgt misschien een vliegende start vanaf de andere kant van de wereld
Hoofdlijnen
- Wat hebben alle levende organismen gemeen?
- Waarom kan je jezelf niet kietelen?
- Wat is het Genotype voor de Roan-kleur?
- Een zwaartekrachttheorie ontwikkelen voor ecologie
- Wanneer dupliceren chromosomen tijdens een cellevenscyclus?
- Seizoensgebonden afbeeldingen onthullen de wetenschap achter stamcellen
- Welk einde is typisch te vinden aan het einde van de enzymnamen?
- Nieuwe analyse plaatst Hobbit op onverwachte ledemaat van de menselijke stamboom
- Celsignalen die wondgenezing in gang zetten zijn verrassend complex
 Wat is een homoloog allel?
Wat is een homoloog allel?  Metagenomische analysesoftware onthult nieuwe oorzaken van het ontstaan van superbacteriën
Metagenomische analysesoftware onthult nieuwe oorzaken van het ontstaan van superbacteriën Hoe de La Brea-teerputten werken
Hoe de La Brea-teerputten werken  Verbazingwekkende resultaten uitgelegd - een multiband-benadering van Coulomb-weerstand en indirecte excitonen
Verbazingwekkende resultaten uitgelegd - een multiband-benadering van Coulomb-weerstand en indirecte excitonen Gesprekken over technische belastingen productief:Mnuchin
Gesprekken over technische belastingen productief:Mnuchin De eigenschappen van nitrocellulose
De eigenschappen van nitrocellulose  Een mijlpaalplan voor het realiseren van fusie-energie en het bevorderen van plasmawetenschap
Een mijlpaalplan voor het realiseren van fusie-energie en het bevorderen van plasmawetenschap Onderzoek werpt nieuw licht op nederzettingen op grote hoogte in Tibet
Onderzoek werpt nieuw licht op nederzettingen op grote hoogte in Tibet
- Elektronica
- Biologie
- Zonsverduistering
- Wiskunde
- French | Italian | Spanish | Portuguese | Swedish | German | Dutch | Danish | Norway |

-
Wetenschap © https://nl.scienceaq.com






