Wetenschap
Het begin van het einde van de orde:experimenten bewijzen Mermin-Wagner-fluctuaties

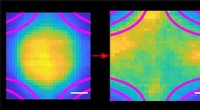
Microscopisch beeld van roostertrillingen in een tweedimensionaal kristal bestaande uit een monolaag van ca. 6, 500 colloïden. Afwijkingen van deeltjesposities van ideale roosterplaatsen kunnen worden waargenomen. Als deze afwijkingen (logaritmisch) groeien met de systeemomvang buiten alle limieten, ze zijn het gevolg van Mermin-Wagner-fluctuaties. In een driedimensionaal kristal, deeltjesafstanden zijn vast en afwijkingen zijn beperkt, ongeacht de grootte van het kristal. Krediet:Universiteit van Konstanz
De klassieke natuurkunde stelt dat een kristal bestaat uit perfect geordende deeltjes met een continue symmetrische atomaire structuur. De stelling van Mermin-Wagner uit 1966 brak met deze visie:het stelt dat in eendimensionale en tweedimensionale atomaire structuren (bijvoorbeeld in een atomaire keten of membraan) er geen perfecte ordening van deeltjes over lange afstanden kan zijn.
Nutsvoorzieningen, 50 jaar later, een groep natuurkundigen uit Konstanz onder leiding van dr. Peter Keim, waren in staat om de stelling van Mermin-Wagner te bewijzen door experimenten en computersimulaties - tegelijkertijd met twee internationale werkgroepen uit Japan en de VS. De onderzoeksresultaten zijn gepubliceerd in de editie van 21 februari 2017 van de Proceedings van de National Academy of Sciences ( PNAS ) wetenschappelijk tijdschrift.
Gebaseerd op een modelsysteem van colloïden, Peter Keim kon bewijzen dat in laagdimensionale systemen langzame maar gestaag groeiende fluctuaties optreden in de afstand tussen deeltjes:de posities wijken af van perfecte roosterplaatsen, afstanden nemen vaak toe of af. Kristalvorming over lange afstanden is daarom niet mogelijk in laagdimensionale materialen.
"Vaak is de stelling van Mermin-Wagner zo geïnterpreteerd dat er helemaal geen kristallen bestaan in tweedimensionale systemen. Dit is verkeerd:in feite groeien langegolfdichtheidsfluctuaties logaritmisch in tweedimensionale systemen en vernietigen ze de orde alleen over lange afstanden , " legt Peter Keim uit. In kleine systemen van slechts een paar honderd deeltjes, kristalvorming kan inderdaad optreden. Maar hoe groter de systemen, hoe meer de onregelmatigheden in de positie van de deeltjes groeien, uiteindelijk voorkomen van kristalvorming over lange afstanden. Peter Keim kon ook de groeisnelheid van deze fluctuaties meten:hij observeerde de voorspelde logaritmische groei, de langzaamst mogelijke vorm van een monotone toename. "Echter, de verstoring van de orde heeft niet alleen een structurele impact, maar laat ook sporen na in de dynamiek van de deeltjes, ’ vervolgt Keim.
De stelling van Mermin-Wagner is een van de standaardonderwerpen van belang in de statistische fysica en werd onlangs opnieuw onderwerp van discussie in het kader van de Nobelprijs voor de natuurkunde:Michael Kosterlitz, de Nobelprijswinnaar van 2016 publiceerde in een commentaar hoe hij en David Thouless gemotiveerd raakten om zogenaamde topologische faseovergangen in laagdimensionale materialen te onderzoeken:het was de tegenstelling tussen de stelling van Mermin-Wagner die het bestaan van perfecte laagdimensionale kristallen verbiedt , enerzijds en de eerste computersimulaties die desondanks kristallisatie in twee dimensies aangaven anderzijds. Het bewijs van Peter Keim en zijn onderzoeksteam heeft nu deze schijnbare tegenstrijdigheid opgelost:op korte schalen is kristalvorming inderdaad mogelijk, maar onmogelijk over lange afstanden.
Het in Konstanz gebaseerde project analyseert gegevens van vier generaties proefschriften. De Mermin-Wagner-fluctuaties werden met succes bewezen door de dynamiek in ongeordende, amorf, dat betekent glazig, tweedimensionale vaste stoffen - net als in het werk uit Japan en de VS dat bijna tegelijkertijd verscheen - terwijl het bestaan van Mermin-Wagner-fluctuaties in tweedimensionale kristallen nog steeds niet direct is bewezen. Het Konstanz-onderzoek werd gesponsord door de Duitse Onderzoeksstichting (DFG) en het Young Scholar Fund van de Universiteit van Konstanz.
 Onderzoekers:Sierra Nevada is de thuisbasis van het oudste ondergrondse watervulsysteem in Europa
Onderzoekers:Sierra Nevada is de thuisbasis van het oudste ondergrondse watervulsysteem in Europa overstromingen, aardverschuivingen doden 37 in Vietnam, scores ontbreken
overstromingen, aardverschuivingen doden 37 in Vietnam, scores ontbreken Hoe FIPEL-lampen werken
Hoe FIPEL-lampen werken  Waarom groene obligaties de sleutel kunnen zijn in de strijd tegen klimaatverandering
Waarom groene obligaties de sleutel kunnen zijn in de strijd tegen klimaatverandering Hoe vond de vroege mensachtigen voedsel tijdens de Oude Steentijd?
Hoe vond de vroege mensachtigen voedsel tijdens de Oude Steentijd?
Hoofdlijnen
- De evolutionaire klok terugdraaien op een lichtgevoelig eiwit
- Vier klassen van macromoleculen belangrijk voor levende dingen
- Onkruidverdelger glyfosaat, controversieel maar nog steeds het meest gebruikt
- Klimaatverandering:kunnen kolibries de hitte aan?
- Dood door duizend sneden? Niet voor kleine populaties
- Het effect van zout en suiker op gedehydrateerde cellen
- Waarom hebben de meeste mensen 23 paar chromosomen?
- Projectideeën om het menselijk spijsverteringssysteem op de middelbare school voor studenten te laten zien
- Relaties tussen mitose in eukaryote cellen en binaire fissie in Prokaryoten
 De omtrek van een kwadrant
De omtrek van een kwadrant Het effect van waterverontreiniging op het land
Het effect van waterverontreiniging op het land  Hoe de natuurlijke glazuren op de muren van Kimberley-rotsschuilplaatsen helpen de wereld te onthullen waarin de kunstenaars leefden
Hoe de natuurlijke glazuren op de muren van Kimberley-rotsschuilplaatsen helpen de wereld te onthullen waarin de kunstenaars leefden Olie belemmert het vermogen van koraalrifvissen om huizen te vinden en roofdieren te ontwijken
Olie belemmert het vermogen van koraalrifvissen om huizen te vinden en roofdieren te ontwijken Coronavirus gebonden? Een perfect project:maak een back-up van uw gegevens
Coronavirus gebonden? Een perfect project:maak een back-up van uw gegevens Aziatische watertorens met krapper budget ondanks warmer en natter klimaat
Aziatische watertorens met krapper budget ondanks warmer en natter klimaat Effecten van plantdata van bodembedekkers op bodemeigenschappen na 4 jaar
Effecten van plantdata van bodembedekkers op bodemeigenschappen na 4 jaar Zilveren nanodeeltjes op grafeenoxidedrager
Zilveren nanodeeltjes op grafeenoxidedrager
- Elektronica
- Biologie
- Zonsverduistering
- Wiskunde
- French | Italian | Spanish | Portuguese | Swedish | German | Dutch | Danish | Norway |

-
Wetenschap © https://nl.scienceaq.com