
Wetenschap
Welke frequentie komt overeen met de reactielijn bij 460 nm?
$$\nu =\frac{c}{\lambda}$$
waar:
- \(\nu\) is de frequentie in Hertz (Hz)
- \(c\) is de lichtsnelheid in meter per seconde (m/s), wat ongeveer \(2,998 \times 10^8\) m/s is
- \(\lambda\) is de golflengte in meter (m)
Gegeven dat de reactielijn zich op 460 nm bevindt, moeten we deze omrekenen naar meters:
$$ \lambda =460 \text{ nm} =460 \times 10^{-9} \text{ m}$$
Door de waarden in de formule te vervangen, kunnen we de frequentie berekenen:
$$ \nu =\frac{2,998 \times 10^8 \text{ m/s}}{460 \times 10^{-9} \text{ m}} \circa 6,52 \times 10^{14} \text {Hz}$$
Daarom is de frequentie die overeenkomt met de reactielijn bij 460 nm ongeveer \(6,52 \maal 10^{14} \) Hz.
 Hoe kan oppervlaktemorfologie de selectiviteit bij elektrokatalyse veranderen?
Hoe kan oppervlaktemorfologie de selectiviteit bij elektrokatalyse veranderen?  Groen licht voor een nieuwe generatie dynamische materialen
Groen licht voor een nieuwe generatie dynamische materialen Slimme stoffen mogelijk gemaakt door nieuwe metaaldepositietechniek
Slimme stoffen mogelijk gemaakt door nieuwe metaaldepositietechniek Mager elektrolytontwerp is een game-changer voor magnesiumbatterijen
Mager elektrolytontwerp is een game-changer voor magnesiumbatterijen Vraag en antwoord:het fascinerende achtergrondverhaal van het periodiek systeem, die op het punt staat 150 jaar te worden
Vraag en antwoord:het fascinerende achtergrondverhaal van het periodiek systeem, die op het punt staat 150 jaar te worden
Hoofdlijnen
- Kunstmatige intelligentie helpt wetenschappers planten te ontwikkelen om de klimaatverandering te bestrijden
- Chimpanseepopulaties vertonen een grote genetische diversiteit, met gevolgen voor het natuurbehoud
- Waarom cellen zure lysosomen nodig hebben
- Waarom leggen boomkikkers hun eieren op de grond?
- Uit onderzoek blijkt dat celkannibalisme en aanverwante verschijnselen in de levensboom wijdverbreid zijn
- Waarom zijn we gewelddadig?
- Hoe verdedigen tuinbouwgewassen zich tegen schimmelpathogenen?
- De voor- en nadelen van klonen
- Wat kan ervoor zorgen dat de celcyclus ongecontroleerd raakt?
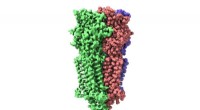
- Cryo-EM onthult structuur en mechanisme van de 5-HT3-receptor
- Sterke constructies realiseren met koolstofvezelversterkte kunststoffen

- Onderzoekers creëren kunstmatige organellen om cellulair gedrag te controleren
- Hoe langzamer ze draaien, hoe helderder ze gloeien

- Hoe computers op zoek zijn naar drugs van de toekomst

 Impact van klimaatverandering op microbiële biodiversiteit hangt af van milieukwaliteit
Impact van klimaatverandering op microbiële biodiversiteit hangt af van milieukwaliteit Lessen van Columbine:Nieuwe technologie geeft inzicht tijdens actieve schietsituaties
Lessen van Columbine:Nieuwe technologie geeft inzicht tijdens actieve schietsituaties Een jaar verder, Caribische eilanden dragen littekens van orkaan Irma
Een jaar verder, Caribische eilanden dragen littekens van orkaan Irma Een verspild decennium:de resterende tijd voor klimaatactie is in 10 jaar met tweederde gekrompen
Een verspild decennium:de resterende tijd voor klimaatactie is in 10 jaar met tweederde gekrompen Het Antropoceen-tijdperk dat niet is – wat de beslissing is om geen nieuw geologisch middel te noemen voor de toekomst van de aarde
Het Antropoceen-tijdperk dat niet is – wat de beslissing is om geen nieuw geologisch middel te noemen voor de toekomst van de aarde  Onderzoekers ontwikkelen nieuwe ultrasnelle 3D-microscoop
Onderzoekers ontwikkelen nieuwe ultrasnelle 3D-microscoop Hoe luchthavenbeveiliging werkt
Hoe luchthavenbeveiliging werkt  Nieuwe technologie verlicht microben die niet in een laboratorium kunnen worden gekweekt
Nieuwe technologie verlicht microben die niet in een laboratorium kunnen worden gekweekt
- Elektronica
- Biologie
- Zonsverduistering
- Wiskunde
- French | Italian | Spanish | Portuguese | Swedish | German | Dutch | Danish | Norway |

-
Wetenschap © https://nl.scienceaq.com

