
Wetenschap
Hoe stel je de vergelijking op om de concentraties van zilverionen en bromide te bepalen, gegeven de gebalanceerde AgBr Ag Br-Ksp-waarde bij 25 graden is 5x10-13?
Gebalanceerde chemische vergelijking:
AgBr(s) ⇌ Ag+(aq) + Br-(aq)
De oplosbaarheidsproductconstante wordt gedefinieerd door:
$$K_{sp} =[\text{Ag}^+] [\text{Br}^-]$$
Waar [Ag^+] en [Br^-] respectievelijk de evenwichtsconcentraties van zilver- en bromide-ionen vertegenwoordigen.
Gegeven \(K_{sp} =5 \times 10^{-13}\) bij \(25 \degree C\), kunnen we de volgende ICE-tabel (Initial, Change, Equilibrium) opstellen om de evenwichtsconcentraties van zilver- en bromide-ionen:
ICE-tabel :
| Soort | Initiaal (M) | Verandering (M) | Evenwicht (M) |
|---|---|---|---|
| AgBr(s) | - | - | - |
| Ag+(aq) | 0 | +x | x |
| Br-(aq) | 0 | +x | x |
Omdat AgBr \(1:1\) oplost, zal de verandering in de concentratie van Ag+ en Br--ionen gelijk zijn, weergegeven als \(+\text x\) en \(-\text x\).
Vervanging van de evenwichtsconcentraties in de \(K_{sp}\) uitdrukking:
$$5 \times 10^{-13} =[\text{x}][\text{x}]$$
Als we \([\text{x}]\ oplossen), verkrijgen we:
$$x =[\text{Ag}^+] =[\text{Br}^-] =\sqrt{5 \times 10^{-13} \ M}$$
Daarom zijn de evenwichtsconcentraties van zilver- en bromide-ionen:
$$[\text{Ag}^+] =[\text{Br}^-] =\sqrt{5 \times 10^{-13} \ M} \circa 2,24 \times 10^{-7}\ M $$
 Waarom tapdansen vervende gifkikkers?
Waarom tapdansen vervende gifkikkers?  Nieuw onderzoek levert supersterke aluminiumlegering op
Nieuw onderzoek levert supersterke aluminiumlegering op Het milieu en de farmaceutische producten voor persoonlijke verzorging:wat zijn de grote vragen?
Het milieu en de farmaceutische producten voor persoonlijke verzorging:wat zijn de grote vragen?  De energieniveaus van organische halfgeleiders afstemmen
De energieniveaus van organische halfgeleiders afstemmen Wat is het mengsel van voornamelijk stikstof en zuurstof?
Wat is het mengsel van voornamelijk stikstof en zuurstof?
 NASA ziet een verminderde, maar doordrenkende ex-tropische cycloon Don
NASA ziet een verminderde, maar doordrenkende ex-tropische cycloon Don Hoe onderscheid te maken tussen een mannelijke en vrouwelijke mus
Hoe onderscheid te maken tussen een mannelijke en vrouwelijke mus De wereld moet actie ondernemen om de golf van vervuilend afval een halt toe te roepen, waarschuwt de VN
De wereld moet actie ondernemen om de golf van vervuilend afval een halt toe te roepen, waarschuwt de VN  Het beleid van Trump zal gemeenschappen die afhankelijk zijn van steenkool schaden in plaats van ze te helpen
Het beleid van Trump zal gemeenschappen die afhankelijk zijn van steenkool schaden in plaats van ze te helpen Canada wil klimaatdoelstelling 2030 halen zegt Trudeau
Canada wil klimaatdoelstelling 2030 halen zegt Trudeau
Hoofdlijnen
- Een spinnenzijde-geluidssysteem:webben passen bij de akoestische deeltjessnelheid voor geluidsdetectie over lange afstanden
- Lijst met waterverontreinigende stoffen
- Opruiming om te overleven onder de zeebodem
- Onderzoekers volgen hoe sporen uit de slapende toestand ontsnappen
- De oproepen van pinguïns worden beïnvloed door hun leefgebied
- Heeft bot het zuur verlicht bij vroege landcrawlers?
- De primaire primaire productiviteit berekenen
- Wat zijn de kansen? Waarschijnlijkheid lost een evolutionaire puzzel op
- Fossiele visvangst uit China bevat oudste tanden ooit
- Nieuw onderzoek naar het potentieel van groene thee om COVID-19 aan te pakken

- Water vormt ruggengraat van hydratatie rond DNA, groepsvondsten

- Het verhaal achter oneindig recyclebaar plastic

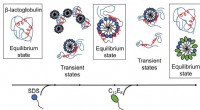
- Met zeep betrapt:begrijpen hoe zeepmoleculen eiwitten helpen om in en uit vorm te komen
- Nieuwe katalysator maakt styreenproductie goedkoper, groener

 Tijdwaarnemingstheorie combineert kwantumklokken en Einsteins relativiteit
Tijdwaarnemingstheorie combineert kwantumklokken en Einsteins relativiteit De ontwikkeling van fusie-energie versnellen om onbeperkte energie op aarde te creëren
De ontwikkeling van fusie-energie versnellen om onbeperkte energie op aarde te creëren Een gestroomlijnde benadering voor het bepalen van thermische eigenschappen van kristallijne vaste stoffen en legeringen
Een gestroomlijnde benadering voor het bepalen van thermische eigenschappen van kristallijne vaste stoffen en legeringen Breuken op een getallenlijn plaatsen
Breuken op een getallenlijn plaatsen Doorbraak in gedrukte elektronica kan leiden tot flexibele elektronicarevolutie
Doorbraak in gedrukte elektronica kan leiden tot flexibele elektronicarevolutie OCTN:een transporter met relevantie voor menselijke pathofysiologie, ontdekking en diagnostiek van geneesmiddelen
OCTN:een transporter met relevantie voor menselijke pathofysiologie, ontdekking en diagnostiek van geneesmiddelen Onderzoekers ontdekken hoe te veel zuurstof cellen en weefsels beschadigt
Onderzoekers ontdekken hoe te veel zuurstof cellen en weefsels beschadigt  Onderzoekers gebruiken AI om de beeldkwaliteit van metalen camera's te verbeteren
Onderzoekers gebruiken AI om de beeldkwaliteit van metalen camera's te verbeteren
- Elektronica
- Biologie
- Zonsverduistering
- Wiskunde
- French | Italian | Spanish | Portuguese | Swedish | German | Dutch | Danish | Norway |

-
Wetenschap © https://nl.scienceaq.com

