
Wetenschap
Wat betekent in de wetenschap?
Hier is hoe het werkt:
1. Tel alle nummers in de set op.
2. Deel de som door het totale aantal waarden.
Het resultaat is het gemiddelde, vaak het gemiddelde genoemd .
Hier is een voorbeeld:
Stel je voor dat je de hoogten van vijf studenten meet:160 cm, 170 cm, 165 cm, 175 cm en 168 cm.
* som: 160 + 170 + 165 + 175 + 168 =838cm
* Aantal waarden: 5
* Gemiddeld: 838 /5 =167,6 cm
Daarom is de gemiddelde hoogte van de vijf studenten 167,6 cm.
Soorten middelen:
Er zijn verschillende soorten middelen, elk geschikt voor specifieke gegevens:
* Rekenkundig gemiddelde: Het meest voorkomende type, berekend zoals hierboven beschreven.
* Geometrische gemiddelde: Gebruikt voor gegevens die exponentieel groeien.
* Harmonisch gemiddelde: Handig voor gegevens die percentages of ratio's omvatten.
Waarom is het gemiddelde belangrijk in de wetenschap?
* Gegevens samenvatten: Het gemiddelde biedt een beknopte manier om een grote dataset weer te geven.
* Vergelijking: Het vergelijken van middelen over verschillende groepen helpt conclusies te trekken over trends en verschillen.
* Statistische analyse: Veel statistische tests zijn afhankelijk van het gemiddelde als een centrale parameter.
Beperkingen van het gemiddelde:
* uitbijters: Extreme waarden (uitbijters) kunnen het gemiddelde aanzienlijk beïnvloeden.
* scheefheid: Scheve gegevens mogen mogelijk niet nauwkeurig de "typische" waarde weergeven met alleen het gemiddelde.
* Niet altijd geschikt: Het gemiddelde is misschien niet de beste maat voor de centrale neiging voor alle gegevenssets.
Vergeet niet dat het gemiddelde een nuttig hulpmiddel is voor het samenvatten van gegevens, maar het is belangrijk om de beperkingen ervan te overwegen en de juiste maatregel te kiezen voor uw specifieke onderzoeksbehoeften.
 Nieuwe biosensor stimuleert zweet terwijl de patiënt koel is en rust
Nieuwe biosensor stimuleert zweet terwijl de patiënt koel is en rust Wordt Cl2 bij elkaar gehouden door ionische binding?
Wordt Cl2 bij elkaar gehouden door ionische binding?  Als je olie in een kopje water giet, zal het gif dan water geven?
Als je olie in een kopje water giet, zal het gif dan water geven?  Welk instrument wordt gebruikt om radioactieve materie te detecteren?
Welk instrument wordt gebruikt om radioactieve materie te detecteren?  Waterflessen, andere gerecyclede 3D-printmaterialen kunnen problemen met militaire bevoorrading voorkomen
Waterflessen, andere gerecyclede 3D-printmaterialen kunnen problemen met militaire bevoorrading voorkomen
 Nieuwe studie onthult toegenomen sneeuwval op Antarctica in de afgelopen twee eeuwen
Nieuwe studie onthult toegenomen sneeuwval op Antarctica in de afgelopen twee eeuwen India zou kunnen voldoen aan de luchtkwaliteitsnormen door het brandstofverbruik van huishoudens te verminderen
India zou kunnen voldoen aan de luchtkwaliteitsnormen door het brandstofverbruik van huishoudens te verminderen Geïntegreerde trajecten om klimaatdoelstellingen te halen en toegang tot veilig water te garanderen
Geïntegreerde trajecten om klimaatdoelstellingen te halen en toegang tot veilig water te garanderen Wat is alles wat een organisme doet en nodig heeft in zijn ecosysteem?
Wat is alles wat een organisme doet en nodig heeft in zijn ecosysteem?  Hoe beïnvloedt pollutie dolfijnen?
Hoe beïnvloedt pollutie dolfijnen?
Hoofdlijnen
- Eigenschap die de kans op een soort verbetert om te overleven?
- Wat zijn de drie basistypen fruit?
- Waarom is een embryo minder vatbaar voor teratogenen per implantatie?
- Je lichaam aan: een hittegolf
- Waarom walvissen geen hersenbeschadiging oplopen als ze zwemmen
- Wat is groeiontwikkeling en reproductie?
- Hoe verschilt glucose van sucrose en cellulosezetmeel?
- Waarom wordt de wetenschap de koningin van alle onderwerpen genoemd?
- Welk phylum hoort een luizen?
- Britse rundvleesboeren willen overstappen naar netto nul, maar praktische en financiële belemmeringen staan in de weg

- Hoe een eiwit vrijkomt om dodelijke kankers te veroorzaken
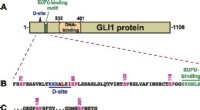
- Hoe orang-oetanmoeders communiceren met hun kroost

- Campylobacter gebruikt andere organismen als Trojaans paard om nieuwe gastheren te infecteren
- Terugtrekkend ijs zorgt ervoor dat Canadese ijsberen een steeds groter risico lopen

 Kan koolmonoxide afkomstig zijn van radiatoren?
Kan koolmonoxide afkomstig zijn van radiatoren?  'S Werelds 22 rijkste mannen hebben meer dan alle vrouwen in Afrika:Oxfam
'S Werelds 22 rijkste mannen hebben meer dan alle vrouwen in Afrika:Oxfam Kunnen sterren ringen om zich heen hebben?
Kunnen sterren ringen om zich heen hebben?  Hoeveel zout doe je erin om het water sneller te laten koken?
Hoeveel zout doe je erin om het water sneller te laten koken?  Wat zijn de kwaliteiten van Stone Samanthakamani?
Wat zijn de kwaliteiten van Stone Samanthakamani?  5 Gebruik van magneten voor kinderen
5 Gebruik van magneten voor kinderen  Hoe aardbevingen de zwaartekracht vervormen
Hoe aardbevingen de zwaartekracht vervormen  Disordered nanonetwerk produceert robuuste en levendige kleuren voor voertuigen, biomimetische weefsels en camouflage
Disordered nanonetwerk produceert robuuste en levendige kleuren voor voertuigen, biomimetische weefsels en camouflage
- Elektronica
- Biologie
- Zonsverduistering
- Wiskunde
- French | Italian | Spanish | Portuguese | Swedish | German | Dutch | Danish | Norway |

-
Wetenschap © https://nl.scienceaq.com

