
Wetenschap
Zes jaar in 120 pagina's:onderzoekers werpen licht op Ricci-stromen
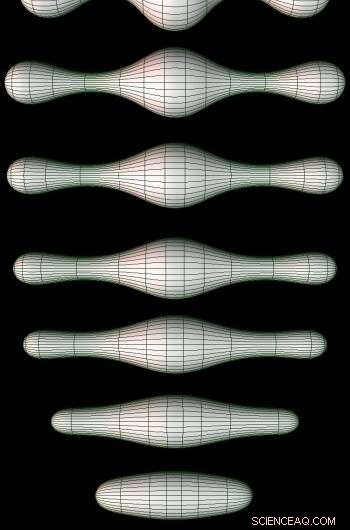
De serval stadia van Ricci Flow op een 2D spruitstuk. Krediet:https://en.wikipedia.org/wiki/Ricci_flow
Differentiële meetkunde is de studie van ruimtemeetkunde. Meerdere natuurlijke fenomenen, van universele uitzetting tot thermische uitzetting en krimp, kan neerkomen op ruimtelijke evolutie. De twee belangrijkste vermoedens op dit gebied, het vermoeden van Hamilton-Tian en de gedeeltelijke C 0 vermoeden, waren onopgeloste puzzels voor meer dan 20 jaar.
"De meeste kiezelstenen op het strand zijn rond. In het begin hadden ze misschien randen en hoeken, maar naarmate de tijd verstrijkt en het tij eb en vloed, hun vorm zal steeds dichter bij perfectie en standaard komen. Maar hoe perfect de evolutie ook is, er kunnen nog afwijkingen zijn, die in de meetkunde 'singulariteiten' worden genoemd."
"Het Hamilton-Tian-vermoeden suggereert dat het grootste deel van de ruimte perfect is, terwijl de grootte van de 'singulariteit' kan worden beperkt tot een laagdimensionale ruimte, " zei prof. Chen Xiuxiong, de oprichter van het Instituut voor Meetkunde en Natuurkunde, Universiteit voor Wetenschap en Technologie van China (USTC) van de Chinese Academie van Wetenschappen (CAS).
Prof Chen, samen met Prof. Wang Bing van USTC, bewees eerst de twee vermoedens.
Hun papier was opgesplitst in 123 pagina's in twee delen van, waarvan de eerste werd gepubliceerd in 2017 en de tweede dit jaar op Journal of Differential Geometry , die ook het fundamentele werk van Hamilton over Ricci-flow publiceerde na een lange cursus van vijf jaar van het ontwikkelen van de theorie en zes jaar van peer-reviewing sinds de eerste inzending.
Dit werk benadrukte de zwakke compactheidstheorie voor niet-ingeklapte Ricci-stromen. Het introduceerde veel innovatieve gedachten en methoden, die verreikende implicaties bijdroeg op het gebied van geometrische analyse, vooral voor de studies van Ricci-stromen.
In feite, veel andere werken zijn ontwikkeld op basis van dit artikel. Bijvoorbeeld, een nieuwe oplossing voor de stabiliteit van het vermoeden van Yau op basis van de structuurtheorie van Ricci-stromen werd gegeven door Prof. Chen, Prof. Wang en Dr. Sun Song van USTC met hun afleiding gepubliceerd in Geometrie en topologie . Daarvoor, ze ontvingen de Oswald Veblen Prize in Geometry voor de eerste oplossing van de stabiliteit van Yau's vermoeden.
De theorie en methoden die in dit artikel worden gepresenteerd, zijn de afgelopen jaren ook toegepast in een reeks werken van Prof. Wang en zijn medewerkers.
De kernideeën van dit artikel werden veralgemeend naar het onderzoek van de gemiddelde krommingsstroom door Prof. Wang en Prof. Li Haozhao, die het extensieprobleem heeft opgelost, en het resultaat werd gepubliceerd in Uitvindingen Mathematicae .
Het artikel van prof. Wang, Dr. Huang Shaosai en Dr. Li Yu, "Over de regelmatige convexiteit van Ricci Shrinker Limit Spaces, " gepubliceerd in Crelle's dagboek , heeft bewezen dat de limiet van niet-ingeklapte krimpende Ricci-solitonen de kegelvorm moet zijn die is gedefinieerd door Prof. Chen en Prof. Wang.
Aanvullend, de krant "Heat Kernel on Ricci Shrinkers, " gepubliceerd in Calculus van variaties en partiële differentiaalvergelijkingen door Prof. Wang en Dr. Li, ontwikkelde verschillende schattingen door de studie van de warmtekernel op Ricci-krimpers en verschafte "noodzakelijke hulpmiddelen om korte tijdsingulariteiten van de Ricci-stromen van algemene dimensie te analyseren."
Deze doorbraak werd gehuldigd door de recensent van het tijdschrift en de winnaar van Fields Metal, Prof. Simon Donaldson, wie zei, "Dit werk is een grote doorbraak in geometrische analyse, en het zal ongetwijfeld leiden tot vele andere gerelateerde onderzoeksprojecten."
 Type energie geproduceerd door fotosynthese
Type energie geproduceerd door fotosynthese Noedels verrijkt met voedingsvezels door geavanceerde technologie blijven lekker
Noedels verrijkt met voedingsvezels door geavanceerde technologie blijven lekker Nieuwe inzichten in schakelbare MOF-structuren
Nieuwe inzichten in schakelbare MOF-structuren Lab-on-paper strook:Klein, goedkoop platform voor het diagnosticeren van tropische koortsen
Lab-on-paper strook:Klein, goedkoop platform voor het diagnosticeren van tropische koortsen Onderzoek naar het creëren van zelfreinigende oppervlakken via 3D-printen
Onderzoek naar het creëren van zelfreinigende oppervlakken via 3D-printen
 Wat zijn de kleuren in pauwenveren?
Wat zijn de kleuren in pauwenveren?  Natuurbeschermers botsen over de weg vooruit ondanks het delen van kerndoelen, studie vondsten
Natuurbeschermers botsen over de weg vooruit ondanks het delen van kerndoelen, studie vondsten Onderzoekers ontwikkelen voorspellend model voor het meten van lachgasemissies in beken en rivieren
Onderzoekers ontwikkelen voorspellend model voor het meten van lachgasemissies in beken en rivieren Bouwstenen van de aarde:onderzoeksteam herberekent distributie van vluchtige elementen
Bouwstenen van de aarde:onderzoeksteam herberekent distributie van vluchtige elementen Tyfoon In-Fa overspoelt Oost-China
Tyfoon In-Fa overspoelt Oost-China
Hoofdlijnen
- Verloren Australische duiker zwom mijlen naar kust gestalkt door haai
- De effecten van algen in drinkwater
- Stiekeme mannetjes nemen vrouwelijke hersens aan om grote bruten voor de gek te houden
- Eukaryotische cel: definitie, structuur en functie (met analogie en diagram)
- Do All Cells Have Mitochondria?
- De verschillen in broederlijke en vaderlijke tweelingen
- Verschillen tussen Protozoa en Protisten
- Micro-evolutie: definitie, proces, micro versus macro & voorbeelden
- Endoplasmatisch reticulum (ruw en glad): structuur en functie (met diagram)
- Cyprus ontdekt eerste ongestoord Romeins scheepswrak

- Nieuwe bronnen bewijzen dat een Fransman een van de vertalers van de King Jamesbijbel was

- Nog steeds op zoek naar Bigfoot

- Experts pleiten voor landelijke adviesraad wetenschappelijke integriteit

- Wereld uitgenodigd om te zien hoe museum Rembrandts Nachtwacht herstelt

 Het percentage dissociatie berekenen
Het percentage dissociatie berekenen  NASA vindt orkaan Delta met zware regenval
NASA vindt orkaan Delta met zware regenval Jeff Bezos Blue Origin lanceert ruimtevaartuig hoger dan ooit
Jeff Bezos Blue Origin lanceert ruimtevaartuig hoger dan ooit Oplossing voor fout in synchrotron-onderzoek kan de resultaten verbeteren
Oplossing voor fout in synchrotron-onderzoek kan de resultaten verbeteren Een nanosensor om dampen te identificeren op basis van een grafeen-silicium heterojunctie Schottky-diode
Een nanosensor om dampen te identificeren op basis van een grafeen-silicium heterojunctie Schottky-diode Groot potentieel voor snellere diagnoses met nieuwe nano-methode
Groot potentieel voor snellere diagnoses met nieuwe nano-methode Hoe een natriumchlorideoplossing te maken
Hoe een natriumchlorideoplossing te maken Schone technologie om chitosan met laag molecuulgewicht te maken
Schone technologie om chitosan met laag molecuulgewicht te maken
- Elektronica
- Biologie
- Zonsverduistering
- Wiskunde
- French | Italian | Spanish | German | Dutch | Danish | Norway | Portuguese | Swedish |

-
Wetenschap © https://nl.scienceaq.com

