
Wetenschap
Wiskundige bespreekt het oplossen van een schijnbaar onoplosbare vergelijking
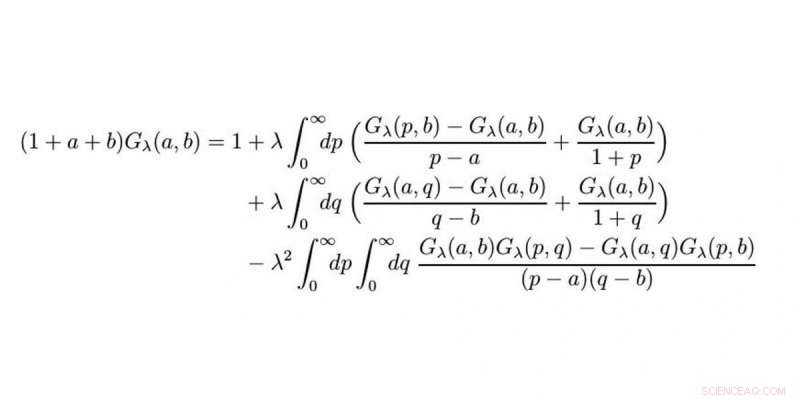
De wiskundige vergelijking. Krediet:WWU/Raimar Wulkenhaar
Na 10 jaar, Prof. Raimar Wulkenhaar van het Mathematisch Instituut van de Universiteit van Münster en zijn collega Dr. Erik Panzer van de Universiteit van Oxford hebben een wiskundige vergelijking opgelost die als onoplosbaar werd beschouwd. De vergelijking moet worden gebruikt om antwoorden te vinden op vragen van de elementaire deeltjesfysica. In dit interview met Christina Heimken, Wulkenhaar kijkt terug op de uitdagingen die we tegenkwamen bij het zoeken naar de formule voor een oplossing en legt uit waarom het werk nog niet klaar is.
Je hebt 10 jaar aan de oplossing van de vergelijking gewerkt. Wat maakte deze vergelijking zo moeilijk op te lossen?
Het is een niet-lineaire integraalvergelijking met twee variabelen. Zo'n vergelijking is zo complex dat je eigenlijk denkt dat er geen formule voor een oplossing kan zijn. Twee variabelen alleen al zijn een uitdaging op zich, en er zijn geen gevestigde benaderingen voor het vinden van een oplossing voor niet-lineaire integraalvergelijkingen. Hoe dan ook, keer op keer gedurende die 10 jaar waren er sprankjes hoop en als resultaat, en ondanks alle moeilijkheden, Ik dacht dat het wel mogelijk was om een expliciete formule voor een oplossing te vinden – uitgedrukt in bekende functies.
Waar kan de vergelijking voor worden gebruikt?
Het gaat over een wiskundig begrip van kwantumveldentheorieën. Deze behoren tot de natuurkunde en spelen een rol bij grootschalige experimenten zoals die bij CERN worden uitgevoerd. Het doel is om elementaire deeltjes wiskundig te beschrijven, d.w.z. de kleinste bekende componenten van materie. Maar dit is zo ingewikkeld dat in plaats daarvan, imaginaire deeltjes worden wiskundig beschreven die bepaalde eigenschappen hebben van de echte deeltjes. De hoop is dat op een dag de echte deeltjes kunnen worden beschreven met behulp van de op deze manier vastgestelde methoden.
Na 10 jaar aan het probleem te hebben gewerkt, je hebt dit jaar een doorbraak meegemaakt. Hoe kwam dat?
Tegen het einde van mei, Ik probeerde een idee uit waarvoor mijn Ph.D. student, Alexander Hock, zorgde voor de beslissende impuls. Ik werkte een nieuwe vergelijking uit - eenvoudiger dan de vorige - en begon deze in lussen op te lossen. Dit betekent dat je de oplossing stap voor stap benadert, d.w.z. lus voor lus, door de linkerkant van de vergelijking in elke vorige stap te berekenen en deze te gebruiken voor de rechterkant van de vergelijking in de volgende stap.
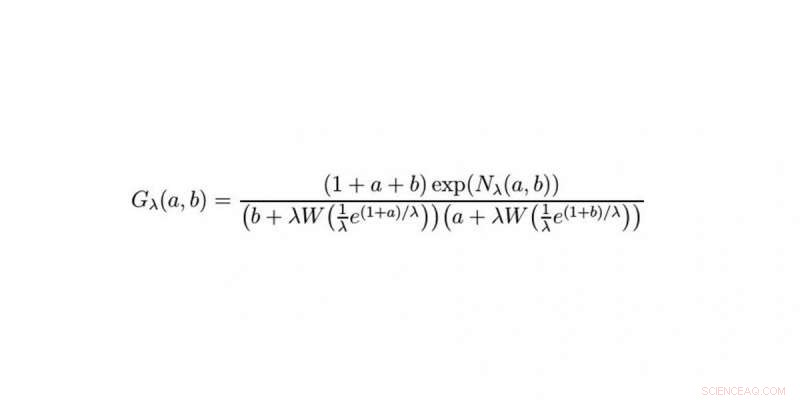
De oplossing. Krediet:WWU/Raimar Wulkenhaar
In de vierde lus moest ik een som van 46 integralen berekenen die oa polylogaritmen bevatten. Deze polylogaritmen, wat enkele van de meer veeleisende functies zijn, werd ingewikkelder in elke lus. Daar heb ik geluk mee gehad, in totaal, bijna alles werd geannuleerd, en wat overbleef was slechts een korte som van machten van normale logaritmen. Ik realiseerde me meteen dat hier een schat te vinden was.
De vijfde lus was niet zo eenvoudig op te lossen - maar opnieuw had ik geluk. Tijdens een zomerschool in de Franse Alpen had ik de gelegenheid om met experts over dergelijke functies te praten. Een van deze experts was Dr. Erik Panzer van de Universiteit van Oxford. Hij had een computerprogramma geschreven over de symbolische wiskunde van hyperlogaritmen en gaf daarbij ondersteuning. 's Nachts heeft dit programma mijn vergelijking doorgerekend tot aan de zevende lus. Het bevestigde mijn resultaten tot en met de vierde lus, en na de vierde lus ging het wonder verder - alles kon worden onderverdeeld in normale logaritmen. Er begon een patroon te ontstaan!
Wat betekent dat?
Misschien herinner je je Pascal's Triangle nog van je schooltijd, met de binominale coëfficiënten? In de driehoek, elk getal dat in een lijn van de driehoek wordt ingevoerd, is de som van de twee getallen die erboven zijn ingevoerd. En het is net zo'n driehoekige structuur die we in onze lussen vinden – zij het ingewikkelder dan in de driehoek van Pascal.
Op 9 juni lussen acht en negen werden voltooid. En toen kwam wat misschien wel het belangrijkste moment was. Erik Panzer ontcijferde een zogenaamde recursieve formule, die elke laatste regel in de driehoek genereert uit de regel erboven, en die ons dus in staat stelt om te extrapoleren van het bekende naar het onbekende.
Wat ging er op dit moment door je heen?
Een van de dingen die ik dacht was, "Niemand kan dit geluk hebben." Ik realiseerde me dat we de vergelijking zouden oplossen. Bij ons avondeten stond er een fles wijn voor onze tafel …
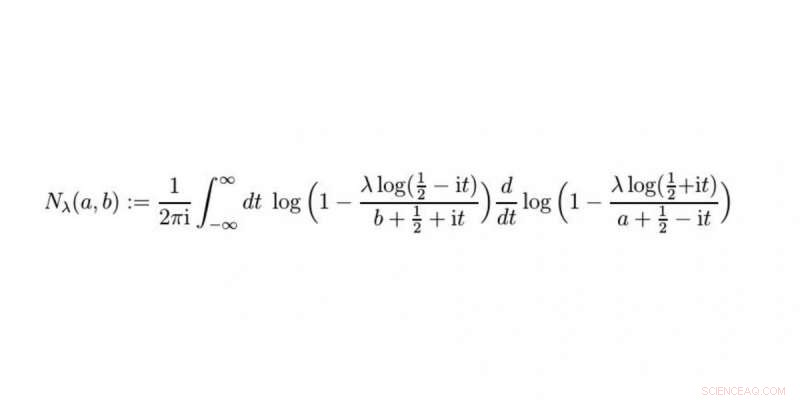
De Nielsen-functie is een deel van de oplossing. Prof. Raimar Wulkenhaar en Dr. Erik Panzer ontdekten deze nieuwe functie tijdens hun werk. Krediet:WWU/Raimar Wulkenhaar
… voordat je weer aan het werk ging.
Ja. De volgende dag slaagde ik erin een deel van de vergelijking terug te brengen tot een eenvoudige reeks afgeleiden. aanvankelijk, de rest leek moeilijk. Pas laat in de avond kwam ik op het idee om de Cauchy-formule te gebruiken om het op te lossen. Ik zette mijn wekker de volgende ochtend op 5.30 uur en probeerde het meteen uit. Het werkte bij de eerste poging, en in de volgende stap stuitte ik op een formule die ik vaak had gezien. Ik wist dat het zou worden opgelost door de Lambert W-functie te gebruiken. Een paar minuten later kreeg ik een e-mail van Erik Panzer:ook hij had aan de Lambert-functie gedacht, maar via een heel andere weg. Als resultaat, we hebben iets bereikt wat al 10 jaar niet haalbaar was:de oplossing van de integraalvergelijking die het model van een kwantumveldentheorie beschrijft. Het was gewoon ongelooflijk.
Je gebruikt ideeën en methoden die in de 18e eeuw door wiskundigen zijn ontwikkeld en die tegenwoordig bijna volledig zijn vergeten.
Deze oude formules hebben ons veel geholpen. De Lambert W-functie, wat een elementair onderdeel is van onze oplossing, is vernoemd naar de Zwitserse wiskundige Johann Heinrich Lambert. Deze vergelijking duikt op in een groot aantal totaal verschillende vragen. Door een gebrek aan kennis van Lamberts grondwerk, de Lambert-functie werd keer op keer uitgevonden, en het werd pas in 1993 als standaard vastgesteld. We gebruikten ook de Lagrange-Bürmann-formule, die ons hielp een integraal op te lossen met behulp van de Lambert-functie, evenals de Cauchy-formule. In het algemeen, wiskunde heeft veel respect voor zijn voorouders. Namen als Euler, Lambertus, Lagrange, Cauchy, Gauss en Hilbert worden geciteerd met de grootste erkenning voor hun prestaties. Maar er zijn twee moderne tools die ik niet zou willen missen:Wikipedia en computeralgebra. Op Wikipedia vind je uitgebreide informatie over bekende – en minder bekende – wiskundige structuren en functies. Computers kunnen vergelijkingen onvergelijkbaar sneller oplossen dan met de hand, en zonder fouten te maken
Wat zijn de volgende stappen?
Er komt een nieuwe functie voor in onze oplossing die we de Nielsen-functie hebben genoemd. Als we het beter hebben begrepen en bijvoorbeeld hebben uitgewerkt hoe het zich verhoudt tot andere bekende functies, wij zullen ons werk – dat als pre-print online vrij toegankelijk is – voor publicatie in een vaktijdschrift met peer reviews aanbieden.
Daarna wil ik graag wat werk voortzetten waar ik sinds 2002 mee bezig ben met mijn collega Prof. Harald Grosse uit Wenen. Het gaat over een kwantumveldentheorie voor wiskundige deeltjes. We zullen dit model nu volledig kunnen begrijpen met behulp van de vergelijking die we hebben opgelost.
 Het potentieel van niet-giftige materialen om lood in perovskietzonnecellen te vervangen
Het potentieel van niet-giftige materialen om lood in perovskietzonnecellen te vervangen Molecuul vliegsnelheid voor het opsporen van drugs
Molecuul vliegsnelheid voor het opsporen van drugs Ingenieurs creëren de meest slijtvaste metaallegering ter wereld
Ingenieurs creëren de meest slijtvaste metaallegering ter wereld Hoe de empirische formule te berekenen
Hoe de empirische formule te berekenen  Koelgordijn gemaakt van een poreus drielaags membraan - alternatief voor elektrisch aangedreven airconditioning
Koelgordijn gemaakt van een poreus drielaags membraan - alternatief voor elektrisch aangedreven airconditioning
 Klimaatwetenschappers bestuderen de kans op een Amerikaanse megadrought
Klimaatwetenschappers bestuderen de kans op een Amerikaanse megadrought Een drievoudige NASA-weergave van orkaan Franklins verdwijnt
Een drievoudige NASA-weergave van orkaan Franklins verdwijnt Natuurlijke verontreinigingsbedreiging voor drinkwater uit grondwater
Natuurlijke verontreinigingsbedreiging voor drinkwater uit grondwater NASA ziet vorming van tropische depressie Two-E in de oostelijke Stille Oceaan
NASA ziet vorming van tropische depressie Two-E in de oostelijke Stille Oceaan Zeespiegelstijging kan bestaande ongelijkheden in de Bay Area verergeren
Zeespiegelstijging kan bestaande ongelijkheden in de Bay Area verergeren
Hoofdlijnen
- De locatie van ribosomen in een cel
- Nieuw apparaat zoomt in op microbengedrag op de juiste schaal
- mRNA: definitie, functie en structuur
- Gespecialiseerde cellen: definitie, soorten en voorbeelden
- Plantenziekte bestrijden bij warme temperaturen houdt voedsel op tafel
- Op zoek naar het CRISPR Zwitsers zakmes
- Belangrijke feiten over het koninkrijk Monera
- Belofte van nieuwe antibiotica ligt in het aanhaken van kleine giftige tetherballs aan bacteriën
- Wat gebeurt er als er geen zuurstof beschikbaar is aan het einde van de langzame glycolyse?
- Heiligdom aan de kant van de Mexicaanse vulkaan zou een universummodel kunnen zijn

- Rapport dringt aan op algemene strategie voor nationale veiligheid en klimaatcrisis

- Inheemse kennis tijdens een pandemie

- Het democratisch bestuur van agrarische multinationals is essentieel voor ecologische duurzaamheid

- Nieuwe studie schetst hoe thuiswerken kan worden aangepast om effectief door te gaan

 Eerst verdween de sneeuw, toen begonnen de modderstromen:Mount Shastas zomer van pijn
Eerst verdween de sneeuw, toen begonnen de modderstromen:Mount Shastas zomer van pijn Duivelse bron van stof in atmosfeer van aarde en Mars
Duivelse bron van stof in atmosfeer van aarde en Mars Internetgemeenschappen kunnen amateurs leren gepersonaliseerde regeringen te bouwen
Internetgemeenschappen kunnen amateurs leren gepersonaliseerde regeringen te bouwen Vissen naar nieuwe antibiotica
Vissen naar nieuwe antibiotica Wat veroorzaakt fotochemische smog?
Wat veroorzaakt fotochemische smog?  Wat zijn enkele van de krachten die landvormen veranderen?
Wat zijn enkele van de krachten die landvormen veranderen?  Een fabriek om te gaan
Een fabriek om te gaan Wat is een subcultuur in de microbiologie?
Wat is een subcultuur in de microbiologie?
- Elektronica
- Biologie
- Zonsverduistering
- Wiskunde
- Italian | Spanish | Swedish | German | Dutch | Danish | Norway | French | Portuguese |

-
Wetenschap © https://nl.scienceaq.com

