
Wetenschap
Een asteroïde van 13 kg reist met snelheid 110 meter als het in 3 gelijke stukken in rust gaat in rust en de tweede gaat verder met hetzelfde wat was energie van explosie?
1. Behoud van momentum
* Voor de explosie: De asteroïde heeft een momentum van (massa * snelheid) =13 kg * 110 m/s =1430 kg * m/s.
* Na de explosie:
* Stuk 1 (in rust):Momentum =0
* Stuk 2 (dezelfde snelheid):momentum =(13 kg/3) * 110 m/s =476,67 kg * m/s
* Stuk 3 (onbekende snelheid):momentum =(13 kg / 3) * V3
Omdat het momentum wordt behouden, is het totale momentum eerder gelijk aan het totale momentum na:
1430 kg*m/s =0 + 476.67 kg*m/s + (13 kg/3)*V3
Oplossen voor V3:
V3 =(1430 - 476.67) * (3/13) =273,33 m / s
2. Kinetische energie
* Voor de explosie: Kinetische energie =(1/2) * massa * snelheid^2 =(1/2) * 13 kg * (110 m/s)^2 =78650 j
* Na de explosie:
* Stuk 1:kinetische energie =0
* Stuk 2:kinetische energie =(1/2) * (13 kg/3) * (110 m/s)^2 =25216.67 j
* Stuk 3:kinetische energie =(1/2) * (13 kg/3) * (273.33 m/s)^2 =51433.33 j
3. Energie van explosie
De energie van de explosie is het verschil tussen de totale kinetische energie na de explosie en de kinetische energie vóór de explosie:
Energie van explosie =(25216.67 J + 51433.33 J) - 78650 J = -1999.99 J
Opmerking: Het negatieve teken geeft aan dat de totale kinetische energie * na de explosie afnam. Dit wordt verwacht, omdat een deel van de initiële kinetische energie werd omgezet in andere vormen van energie tijdens de explosie (zoals warmte en geluid).
Daarom is de energie van de explosie ongeveer 2000 J .
 Waarom verdragen ionische verbindingen elektriciteit in water?
Waarom verdragen ionische verbindingen elektriciteit in water?  Is het smeltpunt van broom hoger of lager dan chloor?
Is het smeltpunt van broom hoger of lager dan chloor?  Onderzoeker laat zien hoe additieven het risico op overdracht van Afrikaanse varkenspest via voer kunnen helpen verminderen
Onderzoeker laat zien hoe additieven het risico op overdracht van Afrikaanse varkenspest via voer kunnen helpen verminderen  Waarom vermindert zwaveldioxide terwijl het oxidatiemiddel van het tellurium-dioxide?
Waarom vermindert zwaveldioxide terwijl het oxidatiemiddel van het tellurium-dioxide?  Is zuurstof in water zuur of basisch?
Is zuurstof in water zuur of basisch?
Hoofdlijnen
- Wat is het principe van dominantie en recessiviteit?
- Hoe een virus zijn symmetrische omhulsels vormt
- Cultuur kan verklaren waarom hersenen groter zijn geworden
- Onderzoek onderzoekt energie- en landgebruikspraktijken op Amerikaanse golfbanen
- Verwacht wordt dat AI de geheimen van niet-coderende genen zal ontrafelen
- Waarom groeien de cellen getransformeerd met PUC18 en Plasmide Lux in aanwezigheid van ampicilline?
- Genetische mutatie verantwoordelijk voor nieuw vachtpatroon bij katten in Finland geïdentificeerd
- Onderzoekers lossen het oude mysterie op over hoe fagen pathogene bacteriën ontwapenen
- Wat betekent wetenschap Inguiry?
- Het injecteren van elektronen schokt de 2D-structuur in een nieuw atomair patroon
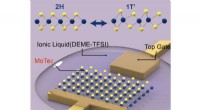
- Het nieuwste nanodraad-experiment vergroot het vertrouwen in de waarneming van Majorana

- In materialen geraakt met licht, individuele atomen en trillingen nemen wanordelijke paden

- CERN:De eerste versnellers zijn weer in actie

- Apparaat genereert UV-spectrumlaserpulsen met een recordbrekende efficiëntie

 Welke eenheid meet kinetische energie?
Welke eenheid meet kinetische energie?  Hoe komt een lopersergie uit de zon?
Hoe komt een lopersergie uit de zon?  Genocidehoax test ethiek van academische publicaties
Genocidehoax test ethiek van academische publicaties In plaats van een standaardlens die de elektronenmicroscoop gebruikt om elektronen te buigen?
In plaats van een standaardlens die de elektronenmicroscoop gebruikt om elektronen te buigen?  Welk heldere object is in de westelijke hemel geweest in Sunset Texas februari 2017?
Welk heldere object is in de westelijke hemel geweest in Sunset Texas februari 2017?  Video:Waarom werkt onkruidverdelger niet meer?
Video:Waarom werkt onkruidverdelger niet meer? Wat is de orbitale hoekmomentumformule en hoe deze in de natuurkunde werd gebruikt?
Wat is de orbitale hoekmomentumformule en hoe deze in de natuurkunde werd gebruikt?  Groenten op Mars binnen tien jaar?
Groenten op Mars binnen tien jaar?
- Elektronica
- Biologie
- Zonsverduistering
- Wiskunde
- French | Italian | Spanish | Portuguese | Swedish | German | Dutch | Danish | Norway |

-
Wetenschap © https://nl.scienceaq.com

