
Wetenschap
Een omhoog naar boven gegooide bal bereikt een hoogte van 13 meter Hoeveel tijd kostte het om zo hoog te worden?
Inzicht in de concepten
* Vrije herfst: Wanneer een object omhoog wordt gegooid, ervaart het een constante neerwaartse versnelling als gevolg van de zwaartekracht (ongeveer 9,8 m/s²).
* Kinematic -vergelijkingen: We zullen een kinematica -vergelijking gebruiken om de hoogte, initiële snelheid, versnelling en tijd te relateren.
De vergelijking
We zullen de volgende kinematische vergelijking gebruiken:
* h =v₀t + (1/2) at²
waar:
* h =laatste hoogte (13 meter)
* V₀ =Initiële snelheid (onbekend)
* t =tijd (wat we willen vinden)
* A =versnelling als gevolg van zwaartekracht (-9,8 m/s² - negatief omdat het naar beneden werkt)
het probleem
We hebben een probleem:we kennen de beginsnelheid niet (v₀). We hebben nog een stuk informatie nodig om dit op te lossen.
Aanvullende informatie nodig
Om de tijd te vinden die de bal nodig heeft om de maximale hoogte te bereiken, hebben we beide nodig:
* De beginsnelheid (v₀) waarmee de bal werd gegooid.
* de tijd die de bal nodig heeft om de maximale hoogte te bereiken en terug te vallen naar zijn startpunt.
Laten we voor tijd oplossen met de beginsnelheid:
1. Op maximale hoogte is de uiteindelijke snelheid van de bal (V) 0 m/s. Dit komt omdat de bal even stopt voordat hij weer naar beneden valt.
2. We kunnen een andere kinematische vergelijking gebruiken om de beginsnelheid te vinden:
* v² =v₀² + 2Ah
* 0² =v₀² + 2 (-9.8) (13)
* v₀² =254.8
* v₀ =√254.8 ≈ 15,96 m/s (dit is de beginsnelheid)
3. Nu kunnen we de eerste vergelijking gebruiken om de tijd te vinden:
* 13 =(15,96) t + (1/2) (-9.8) t²
* 4.9t² - 15.96t + 13 =0
4. Los deze kwadratische vergelijking op voor t:
* U kunt de kwadratische formule of factoring gebruiken. Je krijgt twee oplossingen, maar één zal fysiek onrealistisch zijn. De realistische oplossing is ongeveer t ≈ 1,63 seconden .
Conclusie
Zonder de beginsnelheid of meer informatie kunnen we niet direct de tijd berekenen die de bal nodig heeft om 13 meter te bereiken. Als u de beginsnelheid biedt, kunnen we de tijd vinden.
Hoofdlijnen
- 10 fysieke menselijke eigenschappen die door de evolutie achterhaald zijn
- Beschrijf een reden waarom wetenschapper onderzoek zou kunnen doen?
- Niveaus van celorganisatie
- Hoe anders LJJJJJJJJJJJJJJJJJJJJJJJJJJJJJJJJJJJJJJJJJJJJJJJJJJJJJJJJJJJJJJJJJJJJJJJJJJJJJJJJJJJJJJJJJJJJegJJJJJJJJJJJJJJJJJJJJJJJJJJJJJJJJJJJJJJJJJJJJJJJJJJJJJJJJJJJJJJJJJJJJJ jjjjjjjjjjjjjjjjjjjjjjjjjjjjjjjjjjjjjjjjjjjjjjjjjjjjjjjjjjjjjjjjjjjjjjjjjjjjji
- Wat is het verschil tussen computercel en biologische cel?
- Waarom heterotrofen zijn afhankelijk van autotrofen.
- Wat irriteert een chimpansee?
- Cytoplasma bacteriecellen
- Hoe bepaalt DNA de eigenschappen van een organisme?
- rally's, protesten, en Black Friday:Natuurkunde vindt gevaren die zich in het volle zicht verbergen

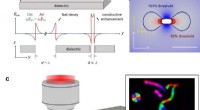
- O-FIB:Far-field-geïnduceerde near-field-afbraak voor direct nanoschrijven in een atmosferische omgeving
- ZnS-scintillatiedetector met uitlezing van golflengteverschuivende vezels

- Hoe ijsbergen echt smelten - en wat dit zou kunnen betekenen voor klimaatverandering

- Diamanten maken gebruik van zowel optische microscopie als MRI voor betere beeldvorming

 Vroegtijdige waarschuwing gezondheids- en welzijnssysteem kan boeren miljoenen ponden besparen
Vroegtijdige waarschuwing gezondheids- en welzijnssysteem kan boeren miljoenen ponden besparen Een holistische kijk op de chemische cyclus van de aarde werpt licht op hoe de planeet bewoonbaar blijft
Een holistische kijk op de chemische cyclus van de aarde werpt licht op hoe de planeet bewoonbaar blijft  Naam 3 gewone mineralen en hoe deze te herkennen?
Naam 3 gewone mineralen en hoe deze te herkennen?  De Beers gaat synthetische diamanten verkopen - zo worden ze gemaakt
De Beers gaat synthetische diamanten verkopen - zo worden ze gemaakt Welke warmteoverdrachtsmethode stelt de aarde in staat energie van de zon te ontvangen?
Welke warmteoverdrachtsmethode stelt de aarde in staat energie van de zon te ontvangen?  Koolstofdioxide bevat koolstof, maar wordt als anorganisch beschouwd, waarom?
Koolstofdioxide bevat koolstof, maar wordt als anorganisch beschouwd, waarom?  Hoe ver zijn de sterren van de grond?
Hoe ver zijn de sterren van de grond?  Fluorescerende techniek brengt verouderende polymeren aan het licht
Fluorescerende techniek brengt verouderende polymeren aan het licht
- Elektronica
- Biologie
- Zonsverduistering
- Wiskunde
- French | Italian | Spanish | Portuguese | Swedish | German | Dutch | Danish | Norway |

-
Wetenschap © https://nl.scienceaq.com


