
Wetenschap
Het negeren van luchtweerstand Wat is de minimale initiële snelheid die een projectiel moet hebben op het oppervlak van de aard als u ontsnapt aan zwaartekrachtspull?
Inzicht in de concepten
* ontsnappingssnelheid: De minimale snelheid die een object nodig heeft om te ontsnappen aan de zwaartekracht van een planeet of ander hemelse lichaam en nooit meer terug te keren.
* Gravitationele potentiële energie: De energie die een object bezit vanwege zijn positie in een zwaartekrachtveld.
* Kinetische energie: De energie die een object bezit vanwege zijn beweging.
De berekening
1. Behoud van energie: De sleutel is om het principe van het behoud van energie te gebruiken. Naarmate het projectiel van de aarde weggaat, neemt de energie van het zwaartekracht toe, terwijl de kinetische energie afneemt. Bij ontsnappingssnelheid zal de kinetische energie van het projectiel nul oneindig ver weg van de aarde zijn.
2. De vergelijking instellen:
* Initiële kinetische energie (KE) + initiële zwaartekrachtpotentiaal energie (GPE) =laatste KE + laatste GPE
* (1/2) mv² - gmm/r =0 + 0
Waar:
* m =massa van het projectiel
* V =ontsnappingssnelheid
* G =zwaartekrachtconstante (6.674 × 10⁻¹¹ m³/kg s²)
* M =massa van de aarde (5.972 × 10²⁴ kg)
* R =straal van aarde (6.371 × 10⁶ m)
3. Oplossing voor ontsnappingssnelheid:
* (1/2) mv² =gmm/r
* v² =2 gm/r
* v =√ (2gm/r)
4. De waarden insluiten:
* v =√ (2 * 6.674 × 10⁻¹¹ m³ / kg s² * 5.972 × 10²⁴ kg / 6.371 × 10⁶ m)
* V ≈ 11,180 m/s
Daarom is de minimale initiële snelheid die een projectiel op het aardoppervlak moet hebben om te ontsnappen aan zwaartekrachttrekkingen (het negeren van luchtweerstand) ongeveer 11.180 m/s (of ongeveer 25.000 mph).
 Kan een mengsel van peper en water ook oplossing worden genoemd?
Kan een mengsel van peper en water ook oplossing worden genoemd?  Wat is de formele lading op het waterstofatoom in HBr?
Wat is de formele lading op het waterstofatoom in HBr?  Is zout en suiker een mengsel of oplossing?
Is zout en suiker een mengsel of oplossing?  Op afstand bestuurde medicijnafgifte implantaatgrootte van druif kan helpen bij het beheer van chronische ziekten
Op afstand bestuurde medicijnafgifte implantaatgrootte van druif kan helpen bij het beheer van chronische ziekten Hoe zijn elektronen verdeeld in een atomen omhulsel?
Hoe zijn elektronen verdeeld in een atomen omhulsel?
 Door de bomen het bos zien:wat een eik ons vertelt over klimaatverandering
Door de bomen het bos zien:wat een eik ons vertelt over klimaatverandering Cloudsat neemt een plak van tropische storm Isaias
Cloudsat neemt een plak van tropische storm Isaias Niet zwaaien, verdrinken:waarom het een kwestie van leven of dood is voor kwelders
Niet zwaaien, verdrinken:waarom het een kwestie van leven of dood is voor kwelders Onderzoek naar klimaatverandering laat zien hoe steden prioriteit kunnen geven aan de volksgezondheid
Onderzoek naar klimaatverandering laat zien hoe steden prioriteit kunnen geven aan de volksgezondheid  Maïsproductiviteit in realtime:Satellieten, veldcamera's, en boeren werken samen
Maïsproductiviteit in realtime:Satellieten, veldcamera's, en boeren werken samen
Hoofdlijnen
- Interspecifieke concurrentie versus intraspecifieke concurrentie
- Genoomonderzoek daagt eerder begrip van de oorsprong van fotosynthese uit
- Onderzoek onderzoekt waarom werknemers vals spelen en hoe bedrijven onbewust aan dit gedrag kunnen bijdragen
- Hebben Cilia en Flagella 1 of 2 membranen?
- Onderzoekers beschrijven hoe sperma de weg kwijt kan raken
- De modificeert eiwitten geleverd van het ruwe endoplasmatische reticulum.
- Wat is eiwit en hoe het heeft gemaakt?
- Hoe helpen de flagella bacteriën rond te bewegen?
- Vroege detectiesysteem voor hinderlijke algenplagende Papahānaumokuākea-riffen
- De waarneming van Kardar-Parisi-Zhang hydrodynamica in een kwantummateriaal

- Nieuwe AR-film ontwikkeld om de transmissie van infrarood licht te maximaliseren

- Knippert helder wanneer hij stevig wordt samengedrukt:hoe eencellige organismen de oceanen verlichten
- Een nieuwe dimensie in de zoektocht naar het begrijpen van donkere materie

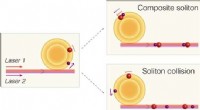
- Botsende solitonen in optische microresonatoren om belangrijke fundamentele fysica te onthullen
 Ammoniakuitstoot veroorzaakt waarschijnlijk geen extreme waas in China
Ammoniakuitstoot veroorzaakt waarschijnlijk geen extreme waas in China Welke 2 elementen vormen brandstof?
Welke 2 elementen vormen brandstof?  Onderzoek in 3D-beeldvorming onthult hoe atomen zijn verpakt in amorfe materialen
Onderzoek in 3D-beeldvorming onthult hoe atomen zijn verpakt in amorfe materialen  Wanneer zandglijdende slangen zich gedragen als lichtgolven
Wanneer zandglijdende slangen zich gedragen als lichtgolven Wat is de oorsprong van minerale hulpbronnen?
Wat is de oorsprong van minerale hulpbronnen?  Grote steden bevorderen sociaal-economische segregatie:zo kunnen we dat oplossen
Grote steden bevorderen sociaal-economische segregatie:zo kunnen we dat oplossen  Waarom jonge mensen misdaad plegen en hoe morele opvoeding kan helpen
Waarom jonge mensen misdaad plegen en hoe morele opvoeding kan helpen Hoe slim te zijn:de 5 beste manieren om slimmer te worden
Hoe slim te zijn:de 5 beste manieren om slimmer te worden
- Elektronica
- Biologie
- Zonsverduistering
- Wiskunde
- French | Italian | Spanish | Portuguese | Swedish | German | Dutch | Danish | Norway |

-
Wetenschap © https://nl.scienceaq.com

