
Wetenschap
Als twee objecten naar elkaar toe liepen met de helft van de snelheid van het licht, bewegen ze dan relatief?
Inzicht in speciale relativiteitstheorie
* Niet eenvoudige toevoeging: Je kunt niet eenvoudig snelheden toevoegen met relativistische snelheden (nabij de snelheid van het licht). Speciale relativiteitstheorie vertelt ons dat tijd en ruimte niet absoluut zijn, maar ten opzichte van het referentiekader van de waarnemer.
* De Lorentz -transformatie: We moeten de Lorentz -transformatie gebruiken om relatieve snelheden correct te berekenen.
Berekening
Laten we zeggen:
* v₁ =0.5c (snelheid van object 1, de helft van de lichtsnelheid)
* v₂ =-0.5c (snelheid van object 2, ook de helft van de snelheid van het licht, maar in de tegenovergestelde richting)
De formule voor het berekenen van de relatieve snelheid (v) van twee objecten die in tegengestelde richtingen bewegen, is:
`` `
v =(v₁ + v₂) / (1 + (v₁ * v₂ / c²)))
`` `
Onze waarden aansluiten:
`` `
v =(0,5c - 0,5c) / (1 + (0,5C * -0,5C / c²)))
v =0 / (1 - 0,25)
v =0 / 0.75
v =0
`` `
resultaat
De relatieve snelheid van de twee objecten is 0 . Dit lijkt misschien contra -intuïtief, maar het is vanwege hoe tijd en ruimte worden beïnvloed met relativistische snelheden. Hoewel elk object met de helft van de snelheid van het licht beweegt, wordt hun relatieve beweging als nul van elkaars referentiekaders gezien.
Sleutelpunt: Hoe snellere objecten bewegen, hoe belangrijker de relativistische effecten worden.
 Met deze techniek kunnen onderzoekers onderzoeken hoe materialen zich op atomair niveau binden
Met deze techniek kunnen onderzoekers onderzoeken hoe materialen zich op atomair niveau binden  Welke twee metalen zijn vloeistof bij kamertemperatuur?
Welke twee metalen zijn vloeistof bij kamertemperatuur?  Krachtige nieuwe beeldvormingsmethode onthult in detail hoe deeltjes in oplossing bewegen
Krachtige nieuwe beeldvormingsmethode onthult in detail hoe deeltjes in oplossing bewegen Wat is het belang van chemie voor de samenleving en het dagelijks leven?
Wat is het belang van chemie voor de samenleving en het dagelijks leven?  Energie besparen bij de productie van chemicaliën
Energie besparen bij de productie van chemicaliën
 Pijpleiding ontspoord, zo is de klimaatstrategie van Canada
Pijpleiding ontspoord, zo is de klimaatstrategie van Canada 3 aardbevingen schudden de grootste stad van Alaska, maar geen schademeldingen
3 aardbevingen schudden de grootste stad van Alaska, maar geen schademeldingen Nieuwe studie kijkt naar handel in stikstofkredieten om de groei van oeverbuffers te stimuleren
Nieuwe studie kijkt naar handel in stikstofkredieten om de groei van oeverbuffers te stimuleren Florence is de tweede natste storm van het land, achter Harvey
Florence is de tweede natste storm van het land, achter Harvey Verhelderend onderzoek onthult hoe planten reageren op licht
Verhelderend onderzoek onthult hoe planten reageren op licht
Hoofdlijnen
- Wat zijn genetisch gemodificeerde organismen (GGO's)? Zijn ze veilig?
- Welke van de volgende macromoleculen omringen en beschermen interne organen?
- Welke celorganellen zijn niet ingebed in cytoplasma -cellen?
- Een neuraal 'navigatiesysteem':hoe zebravissen navigeren om hun comfortabele temperatuur te vinden
- Wat is het biotische potentieel van een vrouwelijke mens?
- Hoe noem je een kleine cel die kan uitgroeien tot nieuwe varen of mos?
- Wat is een anhydrase?
- Wat is het endogene water in het maagdarmkanaal?
- Evenwichtige bemesting:een steunpunt voor duurzame productie van maïs en rijst in Afrika
- Onderzoeksteam ontwikkelt ultrabreedband edge coupler voor zeer efficiënte tweede harmonische generatie

- Onderzoeker documenteert wat er gebeurde tijdens de eerste poging tot een zwaartekrachtsgolfobservatorium in Europa

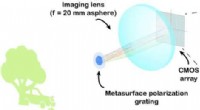
- Draagbare polarisatiegevoelige camera kan worden gebruikt in machinevisie, autonome voertuigen, beveiliging en meer
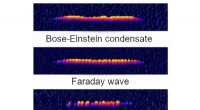
- Materiegolven en kwantumsplinters
- Electron-photon smalltalk kan grote impact hebben op kwantumcomputers

 'Squishy'-lasers kunnen onthullen hoe tumoren en baby's groeien
'Squishy'-lasers kunnen onthullen hoe tumoren en baby's groeien  Hoe hybride werk het management opnieuw uitvindt
Hoe hybride werk het management opnieuw uitvindt  Nieuwe strategie ontworpen voor duurzame productie van benzylamines uit lignine
Nieuwe strategie ontworpen voor duurzame productie van benzylamines uit lignine Welke plaats is de lengtegraad en breedtegraad van 38 North 120 West?
Welke plaats is de lengtegraad en breedtegraad van 38 North 120 West?  30 graden noord en west?
30 graden noord en west?  Snap 20% van het personeelsbestand terwijl de advertentieverkoop blijft opdrogen
Snap 20% van het personeelsbestand terwijl de advertentieverkoop blijft opdrogen Spring Potential Energy: definitie, vergelijking, eenheden (w /voorbeelden)
Spring Potential Energy: definitie, vergelijking, eenheden (w /voorbeelden)  Wat is het belang van cross-over in procesevolutie?
Wat is het belang van cross-over in procesevolutie?
- Elektronica
- Biologie
- Zonsverduistering
- Wiskunde
- French | Italian | Spanish | Portuguese | Swedish | German | Dutch | Danish | Norway |

-
Wetenschap © https://nl.scienceaq.com

