
Wetenschap
Leg uit hoe momentum behouden blijft na een botsing?
Om uit te leggen hoe momentum behouden blijft na een botsing, beschouwen we het vereenvoudigde geval van een eendimensionale botsing tussen twee objecten:
Geval 1:elastische botsing tussen twee bewegende objecten
- Vóór botsing:object 1 met massa m1 en snelheid u1, object 2 met massa m2 en snelheid u2.
- Tijdens botsing:Er wordt aangenomen dat de botsing elastisch is, wat betekent dat er geen verlies aan kinetische energie plaatsvindt. De krachten die betrokken zijn bij de botsing zijn conservatief en veranderen het totale momentum van het systeem niet.
- Na botsing:Object 1 met massa m1 en snelheid v1, object 2 met massa m2 en snelheid v2.
Door het principe van behoud van momentum toe te passen, krijgen we:
```
Totaal aanvankelijk momentum =Totaal eindmomentum
m1u1 + m2u2 =m1v1 + m2v2
```
Omdat de botsing elastisch is, voldoen de relatieve snelheden voor en na de botsing in dit geval aan:
```
(v1 - u1) =(v2 - u2)
```
Door de vergelijking te herschikken, kunnen we zien dat de relatieve beweging tussen de objecten na de botsing onveranderd blijft, waardoor het momentum behouden blijft.
Geval 2:Een inelastische botsing die leidt tot een hechte band
Beschouw een ander scenario waarin de botsing tussen de twee objecten inelastisch is. Na de botsing blijven de objecten aan elkaar plakken en bewegen ze als een samengesteld object.
- Vóór botsing:object 1 met massa m1 en snelheid u1, object 2 met massa m2 en snelheid u2.
- Na botsing:gecombineerd object met massa (m1 + m2) en snelheid v.
Nogmaals, het behoud van momentum toepassen:
```
Totaal aanvankelijk momentum =Totaal eindmomentum
m1u1 + m2u2 =(m1 + m2)v
```
Als we v oplossen, vinden we de snelheid van het gecombineerde object na de botsing:
```
v =(m1u1 + m2u2) / (m1 + m2)
```
In dit geval is de eindsnelheid van het gecombineerde object het gewogen gemiddelde van de beginsnelheden, rekening houdend met de verschillende massa's van de objecten.
Deze voorbeelden illustreren hoe momentum behouden blijft bij botsingen, zowel elastisch als inelastisch. Het principe zorgt ervoor dat het totale momentum van een gesloten systeem onveranderd blijft, ongeacht de krachten die binnen het systeem werken.
 Wat zijn de kleinste deeltjes kleiner dan 3 subatomaire deeltjes?
Wat zijn de kleinste deeltjes kleiner dan 3 subatomaire deeltjes?  Organische verbindingen zijn veelbelovend als goedkopere alternatieven voor metaalfotokatalysatoren
Organische verbindingen zijn veelbelovend als goedkopere alternatieven voor metaalfotokatalysatoren  Door de natuur geïnspireerde proteïne kan helpen bij de plasticplaag
Door de natuur geïnspireerde proteïne kan helpen bij de plasticplaag Wetenschappers ontwikkelen oplossing voor het voorbereiden van macroscopische 2-D MXenes
Wetenschappers ontwikkelen oplossing voor het voorbereiden van macroscopische 2-D MXenes Natuurkundestudent ontwikkelt machine learning-model voor energie- en milieutoepassingen
Natuurkundestudent ontwikkelt machine learning-model voor energie- en milieutoepassingen
 Algen bloeien irk Canarische strandgangers
Algen bloeien irk Canarische strandgangers Word weer mens om sociale, milieu-uitdagingen
Word weer mens om sociale, milieu-uitdagingen Satelliet- en sociaaleconomische gegevens integreren om het klimaatveranderingsbeleid te verbeteren
Satelliet- en sociaaleconomische gegevens integreren om het klimaatveranderingsbeleid te verbeteren tegen 2100, droge steden zullen meer last hebben van hittegolven dan gematigde steden
tegen 2100, droge steden zullen meer last hebben van hittegolven dan gematigde steden Het beperken van de opwarming van de aarde kan miljoenen gevallen van knokkelkoorts voorkomen
Het beperken van de opwarming van de aarde kan miljoenen gevallen van knokkelkoorts voorkomen
Hoofdlijnen
- Eerste onderzoek dat aantoont dat pesticiden morfologische veranderingen bij gewervelde dieren kunnen veroorzaken
- Video:Waarom muizenmaki's bestuderen?
- Kunnen golden retrievers langer leven? Onderzoekers vinden genen die verband houden met een lang leven in het ras
- Waarom zijn organismen opnieuw geclassificeerd?
- Onderzoek toont aan dat cabernet-druiven klimaatverandering kunnen overleven
- Chili vecht om een favoriete mossel te redden
- Hadden dinosaurussen veren?
- Een nieuwe rol voor de eiwitfamilie zou een pad kunnen bieden voor de manier waarop gewaseigenschappen worden gewijzigd
- Heb je katoen? De ontdekking van onderzoekers uit Texas zou eiwitten kunnen opleveren om miljoenen mensen te voeden
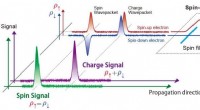
- Spin-resolved oscilloscoop voor laad- en spinsignalen
- Biologische patroonvormende systemen worden beter gekenmerkt door geometrie dan simulaties

- Theoretici ontdekken de Rosetta Stone voor neutrinofysica

- Regelmatige reeksen silicium nanodeeltjes die essentieel zijn voor het verbeteren van de lichtemissie in nanofotonische apparaten

- Verbetering van piëzo-elektrische eigenschappen onder druk
 Hoe ondersteunt de ouderdom van gesteenten op de zeebodem de verspreiding van de theorie?
Hoe ondersteunt de ouderdom van gesteenten op de zeebodem de verspreiding van de theorie?  Herinneringen aan ongelijkheid voor arme mensen prikkelen hen om eerder de rijken te willen belasten
Herinneringen aan ongelijkheid voor arme mensen prikkelen hen om eerder de rijken te willen belasten Zuurstofarme zones in Deense zeeën verdubbelen in een jaar
Zuurstofarme zones in Deense zeeën verdubbelen in een jaar Onderzoek naar machine learning kan veel industrieën helpen
Onderzoek naar machine learning kan veel industrieën helpen Rijsimulatie gebruiken om de zelfgenoegzaamheid van chauffeurs bij passieve spoorwegovergangen te begrijpen
Rijsimulatie gebruiken om de zelfgenoegzaamheid van chauffeurs bij passieve spoorwegovergangen te begrijpen Hoe verschilt Cytokinese bij planten en dieren?
Hoe verschilt Cytokinese bij planten en dieren?  Welke van de volgende sets metingen kan worden gebruikt om de versnelling te berekenen?
Welke van de volgende sets metingen kan worden gebruikt om de versnelling te berekenen?  Zullen tornado's en waterhozen gedijen als de aarde opwarmt?
Zullen tornado's en waterhozen gedijen als de aarde opwarmt?
- Elektronica
- Biologie
- Zonsverduistering
- Wiskunde
- French | Italian | Spanish | Portuguese | Swedish | German | Dutch | Danish | Norway |

-
Wetenschap © https://nl.scienceaq.com

