
Wetenschap
Biologische patroonvormende systemen worden beter gekenmerkt door geometrie dan simulaties

Zoals de collectieve bewegingen van vogelzwermen, de patronen zijn het resultaat van de gecoördineerde interacties van veel individuele deeltjes zonder een centrale coördinator. Krediet:CC0 Publiek Domein
Natuurkundigen van de Ludwig-Maximilians-Universitaet (LMU) in München hebben een nieuwe methode geïntroduceerd waarmee biologische patroonvormende systemen systematisch kunnen worden gekarakteriseerd met behulp van wiskundige analyse. De truc zit hem in het gebruik van geometrie om de dynamiek te karakteriseren.
Veel vitale processen die plaatsvinden in biologische cellen zijn afhankelijk van de vorming van zelforganiserende moleculaire patronen. Bijvoorbeeld, gedefinieerde ruimtelijke verdelingen van specifieke eiwitten reguleren de celdeling, celmigratie en celgroei. Deze patronen zijn het resultaat van de gecoördineerde interacties van vele individuele macromoleculen. Zoals de collectieve bewegingen van vogelzwermen, deze processen hebben geen centrale coördinator nodig. tot nu toe, wiskundige modellering van eiwitpatroonvorming in cellen is grotendeels uitgevoerd door middel van uitgebreide computergebaseerde simulaties. Nutsvoorzieningen, LMU-fysici onder leiding van professor Erwin Frey rapporteren de ontwikkeling van een nieuwe methode die voorziet in de systematische wiskundige analyse van patroonvormingsprocessen, en onthult de hun onderliggende fysieke principes. De nieuwe aanpak wordt beschreven en gevalideerd in een paper dat in het tijdschrift verschijnt Fysieke beoordeling X .
Het onderzoek richt zich op zogenaamde 'massabesparende' systemen, waarbij de interacties de toestanden van de betrokken deeltjes beïnvloeden, maar verander het totale aantal deeltjes in het systeem niet. Aan deze voorwaarde wordt voldaan in systemen waarin eiwitten kunnen schakelen tussen verschillende conformationele toestanden waardoor ze aan een celmembraan kunnen binden of verschillende multicomponentcomplexen kunnen vormen, bijvoorbeeld. Vanwege de complexiteit van de niet-lineaire dynamiek in deze systemen, patroonvorming is tot nu toe bestudeerd met behulp van tijdrovende numerieke simulaties. "Nu kunnen we de meest opvallende kenmerken van patroonvorming begrijpen, onafhankelijk van simulaties met behulp van eenvoudige berekeningen en geometrische constructies, " legt Fridtjof Brauns uit, hoofdauteur van het nieuwe artikel. "De theorie die we in dit rapport presenteren, vormt in wezen een brug tussen de wiskundige modellen en het collectieve gedrag van de systeemcomponenten."
Het belangrijkste inzicht dat tot de theorie leidde, was de erkenning dat veranderingen in de lokale aantaldichtheid van deeltjes ook de posities van lokale chemische evenwichten zullen verschuiven. Deze verschuivingen genereren op hun beurt concentratiegradiënten die de diffuse bewegingen van de deeltjes aandrijven. De auteurs leggen dit dynamische samenspel vast met behulp van geometrische structuren die de globale dynamiek in een multidimensionale 'faseruimte' karakteriseren. omdat deze objecten concrete fysieke betekenissen hebben - als representaties van de banen van verschuivende chemische evenwichten, bijvoorbeeld.
"Dit is de reden waarom onze geometrische beschrijving ons in staat stelt te begrijpen waarom de patronen die we in cellen waarnemen, ontstaan. Met andere woorden, ze onthullen de fysieke mechanismen die het samenspel tussen de betrokken moleculaire soorten bepalen, "zegt Frey. "Bovendien, de fundamentele elementen van onze theorie kunnen worden gegeneraliseerd om met een breed scala aan systemen om te gaan, die op zijn beurt de weg vrijmaakt voor een uitgebreid theoretisch kader voor zelforganiserende systemen."
 Schuifkracht:hoe goede materialen beter worden gemaakt?
Schuifkracht:hoe goede materialen beter worden gemaakt? Hoe beïnvloedt pH-niveau enzymactiviteit?
Hoe beïnvloedt pH-niveau enzymactiviteit?  Chemische synthese zou krachtigere antibiotica kunnen produceren
Chemische synthese zou krachtigere antibiotica kunnen produceren Team ontwikkelt ontbrekende schakel naar circulaire economie en pakt wereldwijde verspilling aan
Team ontwikkelt ontbrekende schakel naar circulaire economie en pakt wereldwijde verspilling aan Neutronenstudie van glaucoommedicijnen biedt aanwijzingen over enzymdoelen voor agressieve kankers
Neutronenstudie van glaucoommedicijnen biedt aanwijzingen over enzymdoelen voor agressieve kankers
 Dodental tyfoon Kammuri loopt op tot vier in Filipijnen
Dodental tyfoon Kammuri loopt op tot vier in Filipijnen Wat is er gebeurd met al het plastic afval in de Indische Oceaan?
Wat is er gebeurd met al het plastic afval in de Indische Oceaan? Microben liften landinwaarts op kustmist
Microben liften landinwaarts op kustmist Niet zo fantastisch:kan Japan zijn liefdesaffaire met plastic beëindigen?
Niet zo fantastisch:kan Japan zijn liefdesaffaire met plastic beëindigen? Ontdekkingsreizigers sturen de eerste live video-uitzending vanuit de diepten van de oceaan
Ontdekkingsreizigers sturen de eerste live video-uitzending vanuit de diepten van de oceaan
Hoofdlijnen
- Microbeads zorgen ervoor dat ultrasone golven cellen veiliger kunnen stimuleren
- Zeldzame vliegende vossen neergeschoten bij gruwelijke aanval in Australië
- Belofte van nieuwe antibiotica ligt in het aanhaken van kleine giftige tetherballs aan bacteriën
- (Her)verwerven van het potentieel om alles te worden
- Een driedimensionaal model van een plantencel maken met labels
- Roofzuchtige bacteriën gevonden in studie van longmicrobioom van patiënten met cystische fibrose
- Insectengedrag bestuderen? Maak van jezelf een ethoscoop
- Voorbeelden van een recessief allel
- Wat zijn de voordelen van Ribosomes?
- Vloeibare kristallen in nanoporiën produceren een verrassend grote negatieve druk

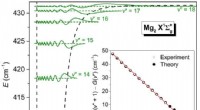
- Kwantumberekening lost een oud raadsel op:de trillingstoestanden van magnesiumdimeer vinden
- Stabiele meerderheden

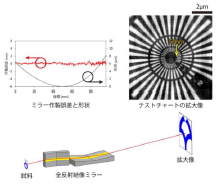
- Röntgenmicroscoopoptiek lost 50 nm-kenmerken op en elimineert chromatische aberraties
- Directe atoom-opgeloste beeldvorming van magnetische materialen

 Polyamoreuze relaties onder zware druk tijdens de pandemie
Polyamoreuze relaties onder zware druk tijdens de pandemie Simulaties van zwarte gaten bieden een blauwdruk voor toekomstige waarnemingen
Simulaties van zwarte gaten bieden een blauwdruk voor toekomstige waarnemingen Broeikasgassen en aerosolemissies verlengen en intensiveren droogtes
Broeikasgassen en aerosolemissies verlengen en intensiveren droogtes MUSE onthult een gloeiende lichtring in het verre heelal
MUSE onthult een gloeiende lichtring in het verre heelal Taalveranderingen in gender- en etnische stereotypen correleerden met grote sociale bewegingen en demografische veranderingen
Taalveranderingen in gender- en etnische stereotypen correleerden met grote sociale bewegingen en demografische veranderingen Botsende protonen frontaal
Botsende protonen frontaal Onderzoekers creëren nieuwe staat van licht
Onderzoekers creëren nieuwe staat van licht Spanje wil digitale belasting invoeren die de VS boos heeft gemaakt
Spanje wil digitale belasting invoeren die de VS boos heeft gemaakt
- Elektronica
- Biologie
- Zonsverduistering
- Wiskunde
- French | Italian | Spanish | Portuguese | Swedish | German | Dutch | Danish | Norway |

-
Wetenschap © https://nl.scienceaq.com

