
Wetenschap
Bewegingsvergelijking afleiden met behulp van het principe?
De bewegingsvergelijkingen van Lagrange zijn een reeks differentiaalvergelijkingen van de tweede orde die de beweging van een systeem van deeltjes beschrijven. Ze zijn afgeleid van het principe van de minste actie, dat stelt dat het daadwerkelijke pad dat een systeem tussen twee punten aflegt, het pad is dat de actie-integraal minimaliseert.
De actie-integraal wordt gedefinieerd als de integraal van de Lagrangiaan in de tijd:
$$S =\int_{t_1}^{t_2} L(q_i, \dot{q_i}, t) dt$$
waarbij $q_i$ de gegeneraliseerde coördinaten van het systeem zijn, $\dot{q_i}$ hun tijdsafgeleiden zijn, en $L$ de Lagrangiaan is. De Lagrangiaan is een functie van de gegeneraliseerde coördinaten, hun tijdsafgeleiden en de tijd.
Het principe van de minste actie stelt dat het daadwerkelijke pad dat een systeem tussen twee punten aflegt, het pad is dat de actie-integraal minimaliseert. Dit kan wiskundig worden uitgedrukt als:
$$\delta S =0$$
waarbij $\delta S$ de variatie van de actie-integraal is.
De bewegingsvergelijkingen van Lagrange kunnen worden afgeleid uit het principe van de minste actie door gebruik te maken van de variatierekening. De variatierekening is een tak van de wiskunde die zich bezighoudt met het vinden van functies die een functionaliteit minimaliseren of maximaliseren.
Om de functies te vinden die de actie-integraal minimaliseren, moeten we de variaties van de actie-integraal vinden en deze gelijk stellen aan nul. De variaties van de actie-integraal worden gegeven door:
$$\delta S =\int_{t_1}^{t_2} \left(\frac{\gedeeltelijk L}{\gedeeltelijk q_i} \delta q_i + \frac{\gedeeltelijk L}{\gedeeltelijk \dot{q_i}} \delta \dot{q_i} + \frac{\gedeeltelijke L}{\gedeeltelijke t} \delta t\right) dt$$
waarbij $\delta q_i$, $\delta \dot{q_i}$ en $\delta t$ de variaties zijn van de gegeneraliseerde coördinaten, hun tijdsafgeleiden en de tijd.
Als we de variaties van de actie-integraal gelijk stellen aan nul, krijgen we:
$$\frac{\gedeeltelijke L}{\gedeeltelijke q_i} =\frac{d}{dt} \left(\frac{\gedeeltelijke L}{\gedeeltelijke \dot{q_i}}\right)$$
Dit zijn de bewegingsvergelijkingen van Lagrange. Het zijn een reeks differentiaalvergelijkingen van de tweede orde die de beweging van een systeem van deeltjes beschrijven.
Voorbeeld:
Beschouw een deeltje met massa $m$ dat beweegt in een eendimensionaal potentieel $V(x)$. De Lagrangiaan voor dit systeem is:
$$L =\frac{1}{2} m \dot{x}^2 - V(x)$$
De gegeneraliseerde coördinaat voor dit systeem is $x$, en de afgeleide naar de tijd is $\dot{x}$. De Lagrangiaan is een functie van $x$, $\dot{x}$ en $t$.
De bewegingsvergelijking van Lagrange voor dit systeem is:
$$\frac{\gedeeltelijke L}{\gedeeltelijke x} =\frac{d}{dt} \left(\frac{\gedeeltelijke L}{\gedeeltelijke \dot{x}}\right)$$
Als we de Lagrangiaan in deze vergelijking vervangen, krijgen we:
$$- \frac{\gedeeltelijk V}{\gedeeltelijk x} =m \frac{d^2 x}{dt^2}$$
Dit is de tweede bewegingswet van Newton voor een deeltje met massa $m$ dat beweegt in een eendimensionaal potentieel $V(x)$.
 Een efficiënte benadering van geconjugeerde tetraenen uit butadieen en alkynen
Een efficiënte benadering van geconjugeerde tetraenen uit butadieen en alkynen Onderzoekers ontwikkelen duurzame energie-aanpak voor de productie van ammoniak
Onderzoekers ontwikkelen duurzame energie-aanpak voor de productie van ammoniak Verandert de geleidbaarheid van water als de suikerconcentratie verandert?
Verandert de geleidbaarheid van water als de suikerconcentratie verandert?  Nieuwe cyclisatiereacties voor het synthetiseren van macrocyclische medicijnleads
Nieuwe cyclisatiereacties voor het synthetiseren van macrocyclische medicijnleads Duidelijk, geleidende coating kan geavanceerde zonnecellen beschermen, aanraakschermen
Duidelijk, geleidende coating kan geavanceerde zonnecellen beschermen, aanraakschermen
Hoofdlijnen
- Stamcelvaccins: de nieuwe grens in kanker-therapie?
- Hoe krijgt een met veroudering geassocieerd enzym toegang tot ons genetisch materiaal?
- Wat is het verschil tussen Ribosoom en Ribosomaal DNA?
- Kan de wetenschap bendemoorden voorspellen?
- Wat is de functie van de huidmondjescel?
- Epitheliale cellen: definitie, functie, typen en voorbeelden
- Hoe gastheercelenzymen het coronavirus bestrijden
- Hoe Brain Mapping werkt
- Het aantal mitochondriale DNA-kopieën draagt bij aan de groeidiversiteit bij allopolyploïde vissen
- De mysteries van supergeleiders onthullen:de nieuwe reikwijdte van Teams wordt nader bekeken

- Voor het eerst waargenomen reactie van een kwantumvloeistof op foto-excitatie van opgeloste deeltjes

- Diamantkleurcentra voor niet-lineaire fotonica
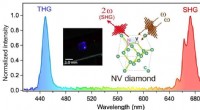
- De ionisatie van door protonen beïnvloed helium begrijpen

- Onderzoekers ontwikkelen een eerste-principes kwantum Monte Carlo-pakket genaamd TurboRVB
 Het is echt moeilijk voor computers om gezond verstand te leren
Het is echt moeilijk voor computers om gezond verstand te leren  Hoe verschilt Cytokinese bij planten en dieren?
Hoe verschilt Cytokinese bij planten en dieren?  De eigenschappen van 2D-materialen ontmaskeren
De eigenschappen van 2D-materialen ontmaskeren Luisteren naar hoe eiwitten praten en hun taal leren
Luisteren naar hoe eiwitten praten en hun taal leren  Ten minste 2% van de openbare watersystemen in de VS zijn als Flints - Amerikanen horen er gewoon niets over
Ten minste 2% van de openbare watersystemen in de VS zijn als Flints - Amerikanen horen er gewoon niets over Welk type binding heeft zwaveldioxide?
Welk type binding heeft zwaveldioxide?  Neutronen schilderen atomair portret van prototypisch celsignaleringsenzym
Neutronen schilderen atomair portret van prototypisch celsignaleringsenzym Modellering van microzwemmers voor medicijnafgifte
Modellering van microzwemmers voor medicijnafgifte
- Elektronica
- Biologie
- Zonsverduistering
- Wiskunde
- French | Italian | Spanish | Portuguese | Swedish | German | Dutch | Danish | Norway |

-
Wetenschap © https://nl.scienceaq.com

