
Wetenschap
Een eenvoudig kwantumdynamicaprobleem?
Oplossing: De Schrödingervergelijking voor dit systeem is:$$-\frac{\hbar^2}{2m}\left ( \frac{\partial^2}{\partial x^2}+\frac{\partial^2}{ \gedeeltelijke y^2} \right )\psi(x,y)+\frac{1}{2}m\omega^2(x^2+y^2)\psi(x,y)=E\psi (x,y)$$
We kunnen de variabelen scheiden en aannemen dat de golffunctie kan worden geschreven als een product van twee functies, $\psi(x,y)=X(x)Y(y)$. Dit vervangen door de Schrödingervergelijking en delen door $ XY$, we krijgen:
$$-\frac{1}{2m}\frac{X''}{X}=\frac{1}{2m}\frac{Y''}{Y}+\frac{1}{2}m \omega^2(x^2+y^2)=E$$
De LHS van deze vergelijking hangt alleen af van x, terwijl de RHS alleen van y afhangt. Daarom moeten beide zijden gelijk zijn aan een constante, die we kunnen aangeven met $E_n$,
$$-\frac{1}{2m}\frac{X''}{X}=E_n , \frac{1}{2m}\frac{Y''}{Y}=E-E_n.$$
Dit zijn twee onafhankelijke eendimensionale harmonische oscillatorproblemen, en hun oplossingen zijn bekend. De energie-eigenwaarden voor de beweging in de x-richting zijn:
$$E_n=\hbar\omega\left(n+\frac{1}{2}\right), n=0,1,2,...$$
Op dezelfde manier worden de energie-eigenwaarden voor de beweging in de y-richting gegeven door dezelfde formule. Daarom zijn de totale energie-eigenwaarden voor het tweedimensionale systeem:
$$E_{n_x,n_y}=\hbar\omega\links(n_x+n_y+1\rechts), n_x,n_y=0,1,2,...$$
De overeenkomstige eigenfuncties zijn producten van de eendimensionale harmonische oscillatorgolffuncties:
$$\psi_{n_x,n_y}(x,y)=\phi_{n_x}(x)\phi_{n_y}(y),$$
waar
$$\phi_n(x)=\frac{1}{\sqrt{2^n n!}}\left(\frac{m\omega}{\pi\hbar}\right)^{1/4}H_n \ left(\sqrt{\frac{m\omega}{\hbar}}x \right) e^{-m\omega x^2/2\hbar},$$
en $H_n$ zijn de Hermite-polynomen.
 Slime voor kinderen maken zonder Borax, kleurstof voor levensmiddelen en witte lijm
Slime voor kinderen maken zonder Borax, kleurstof voor levensmiddelen en witte lijm  Uranium gebruiken om orde te scheppen in wanorde
Uranium gebruiken om orde te scheppen in wanorde Zelfherstellende katalysatorfilms voor waterstofproductie
Zelfherstellende katalysatorfilms voor waterstofproductie Depressie, zwaarlijvigheid, chronische pijn kan worden behandeld door zich op hetzelfde belangrijke eiwit te richten
Depressie, zwaarlijvigheid, chronische pijn kan worden behandeld door zich op hetzelfde belangrijke eiwit te richten Polyester verkrijgen uit plantaardige olie
Polyester verkrijgen uit plantaardige olie
 Hoe duurzame gemeenschappen werken
Hoe duurzame gemeenschappen werken  Methaan:een krachtig gas dat de planeet verwarmt
Methaan:een krachtig gas dat de planeet verwarmt  Onderzoekers vinden natuurlijk voorkomende fotostromen in anorganische minerale systemen
Onderzoekers vinden natuurlijk voorkomende fotostromen in anorganische minerale systemen Uit onderzoek blijkt dat de kliffen aan de kust van Californië afbrokkelen zonder waarneembaar patroon
Uit onderzoek blijkt dat de kliffen aan de kust van Californië afbrokkelen zonder waarneembaar patroon Door klimaat veroorzaakte honger is meer dan verdubbeld in zwaarst getroffen landen:rapport
Door klimaat veroorzaakte honger is meer dan verdubbeld in zwaarst getroffen landen:rapport
Hoofdlijnen
- milities, stropers richten grote schade aan in het wild in Centraal-Afrika:monitor
- Hoe pathogene bacteriën de slingers en pijlen van infectie doorstaan
- Fokresistente kippen voor verbeterde voedselveiligheid
- Voor het ontrafelen van DNA-mysteries ontdekken natuurkundigen letterlijk hoe een essentieel enzym werkt
- Biofysici onthullen hoe drie eiwitten samenwerken om de cellulaire beweging te verfijnen
- Nieuw onderzoek wijst uit dat walvistanden na het midden van de dracht nog steeds aanwezig zijn, wat enigszins verrassend is
- Nieuwe methode bevordert de detectie van kanker door kleine bloedcirculerende deeltjes te tellen
- Kunnen dieren iriserende kleuren gebruiken om te communiceren?
- Machine learning kan wetenschappers helpen begrijpen waarom vogels plastic eten
- Hoe zware elementen in het universum ontstaan

- Volledig geïntegreerde hot qubit-quantumprocessor met commercieel beschikbare technologie

- Een scanning quantum sensing microscoop met elektrische veldbeeldvorming op nanoschaal
- Onderzoekers nemen terahertz-datalinks door de bocht

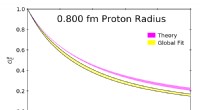
- Natuurkundigen werken samen om protonradiusprobleem aan te pakken
 Wiskundediploma’s worden steeds minder toegankelijk – en dit is een probleem voor het bedrijfsleven, de overheid en innovatie
Wiskundediploma’s worden steeds minder toegankelijk – en dit is een probleem voor het bedrijfsleven, de overheid en innovatie  Wetenschappers laten onderzoekshydrogel meer als biologische weefsels groeien
Wetenschappers laten onderzoekshydrogel meer als biologische weefsels groeien Het beschermen van dieren in het wild begint met inzicht in de beste manier om misdaden tegen te gaan
Het beschermen van dieren in het wild begint met inzicht in de beste manier om misdaden tegen te gaan  Mitosis: definitie, stadia en doel
Mitosis: definitie, stadia en doel  Hoe scholen microzwemmers hun laadcapaciteit kunnen vergroten
Hoe scholen microzwemmers hun laadcapaciteit kunnen vergroten Kenmerken van het ecosysteem
Kenmerken van het ecosysteem  Het succes van een nieuw venture-team vereist collectief eigendom - met grenzen, studie zegt:
Het succes van een nieuw venture-team vereist collectief eigendom - met grenzen, studie zegt: Zeldzame beluga-gegevens laten zien dat walvissen duiken om hun maaltijden te maximaliseren
Zeldzame beluga-gegevens laten zien dat walvissen duiken om hun maaltijden te maximaliseren
- Elektronica
- Biologie
- Zonsverduistering
- Wiskunde
- French | Italian | Spanish | Portuguese | Swedish | German | Dutch | Danish | Norway |

-
Wetenschap © https://nl.scienceaq.com

