
Wetenschap
Het oppervlak weet wat eronder ligt:natuurkundigen laten zien hoe topologische isolatoren van hogere orde kunnen worden gedetecteerd
Topologische materialen zijn een klasse materialen met unieke elektronische eigenschappen die worden beschermd door topologische invarianten. Deze materialen hebben de afgelopen jaren veel belangstelling gekregen vanwege hun potentieel voor het realiseren van nieuwe vormen van kwantummaterie en voor gebruik in toekomstige elektronische apparaten.
Eén type topologisch materiaal is de topologische isolator, een isolatiemateriaal met geleidende oppervlaktetoestanden. Deze oppervlaktetoestanden worden beschermd door een topologische invariant, wat betekent dat ze niet kunnen worden vernietigd zonder de topologische eigenschappen van het materiaal te veranderen.
Topologische isolatoren van hogere orde zijn een generalisatie van topologische isolatoren. Ze hebben topologische invarianten van hogere orde en hun oppervlaktetoestanden vertonen exotische eigenschappen die niet voorkomen in conventionele topologische isolatoren. Het detecteren van topologische isolatoren van hogere orde is echter een uitdagende taak geweest vanwege de complexe aard van hun oppervlaktetoestanden.
In hun onderzoek ontwikkelden de natuurkundigen uit Würzburg en Konstanz een nieuwe methode voor het detecteren van topologische isolatoren van hogere orde. Hun methode omvat het meten van de elektrische geleiding van een materiaal als functie van de dikte ervan. Ze ontdekten dat de geleiding van een topologische isolator van hogere orde een karakteristieke piek vertoont bij een specifieke dikte.
Deze karakteristieke piek is een kenmerk van de oppervlaktetoestanden van de topologische isolator van hogere orde. Door de geleiding van een materiaal te meten, konden de natuurkundigen de aanwezigheid van topologische isolatoren van hogere orde detecteren en deze onderscheiden van andere soorten topologische materialen.
De bevindingen van de natuurkundigen hebben belangrijke implicaties voor het gebied van topologische materialen. Ze bieden een nieuw hulpmiddel voor het detecteren van topologische isolatoren van hogere orde, waardoor onderzoekers deze materialen gedetailleerder kunnen bestuderen en hun potentieel voor toekomstige toepassingen kunnen onderzoeken.
Bovendien kunnen de bevindingen van de natuurkundigen implicaties hebben voor de ontwikkeling van nieuwe elektronische apparaten. Topologische isolatoren van hogere orde kunnen mogelijk worden gebruikt in de spintronica, de studie van hoe de spins van elektronen kunnen worden gebruikt om informatie op te slaan en te verwerken. Ze zouden ook kunnen worden gebruikt in quantum computing, de studie van hoe de kwantumeigenschappen van deeltjes kunnen worden gebruikt om berekeningen uit te voeren.
Het onderzoek van de natuurkundigen betekent een belangrijke stap voorwaarts in het begrip en de detectie van topologische isolatoren van hogere orde. Hun bevindingen hebben het potentieel om nieuwe onderzoeksmogelijkheden te openen op het gebied van topologische materialen en te leiden tot de ontwikkeling van nieuwe toepassingen in spintronica en kwantumcomputers.
 Zeldzame gasvondst lost puzzel op van stijgend landschap in zuidelijk Afrika
Zeldzame gasvondst lost puzzel op van stijgend landschap in zuidelijk Afrika Microben liften landinwaarts op kustmist
Microben liften landinwaarts op kustmist Trakteer jezelf op een storm? Het zit allemaal in de naam
Trakteer jezelf op een storm? Het zit allemaal in de naam  Enorme barrière houdt plastic afval niet vast in de Stille Oceaan
Enorme barrière houdt plastic afval niet vast in de Stille Oceaan Dankzij COVID-19, niets beweegt - en seismologen kunnen het zien
Dankzij COVID-19, niets beweegt - en seismologen kunnen het zien
Hoofdlijnen
- Geen hondenleven voor oudere dieren in Singapore Zoo
- Waarom zijn kalkoenen genetisch gemodificeerd?
- Moleculaire mechanismen van paaigewoonten voor adaptieve straling van endemische Oost-Aziatische karperachtigen
- Een nieuwe studie heeft geconcludeerd dat er geen duidelijk bewijs is dat COVID-19 werd overgedragen door vleermuizen
- Hoe de percentages van adenine in een DNA-streng te berekenen
- Ouders van het jaar:Opruimende roofvogels tonen een hoog niveau van samenwerking bij het grootbrengen van kuikens
- Hoe wild is het Bengaalse kattengenoom?
- Is het levend of dood? Team laat zien hoe je de thermische handtekeningen van afzonderlijke cellen kunt meten
- Verschillen tussen een neuron en een neuroglia
- Natuurkundigen stellen een test voor van kwantumzwaartekracht voor met behulp van de huidige technologie
- Wat is een monomeer?

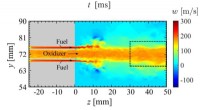
- Brandstofstroom, warmteschommelingen veroorzaken gevaarlijke trillingen in raketmotoren
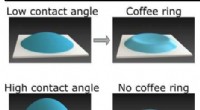
- Internationaal team ontdekt mysterie achter koffieringvorming
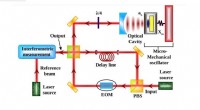
- Optische vezels die de materialen eromheen kunnen voelen

 Koralen kunnen tijdens hun leven verworven mutaties doorgeven aan nakomelingen
Koralen kunnen tijdens hun leven verworven mutaties doorgeven aan nakomelingen Game-changer voor schone waterstofproductie
Game-changer voor schone waterstofproductie De last van het klimaatrisico valt op de armen
De last van het klimaatrisico valt op de armen Bomen die groeien in zout water
Bomen die groeien in zout water Kun je van een auto een broedmachine maken?
Kun je van een auto een broedmachine maken?  Nieuwe vingerafdrukken toegevoegd aan database voor chemische identificatie
Nieuwe vingerafdrukken toegevoegd aan database voor chemische identificatie Europese bedrijven zeggen dat zakendoen in China moeilijker is
Europese bedrijven zeggen dat zakendoen in China moeilijker is Afbeelding:Strook van Saturnus
Afbeelding:Strook van Saturnus
- Elektronica
- Biologie
- Zonsverduistering
- Wiskunde
- French | Italian | Spanish | Portuguese | Swedish | German | Dutch | Danish | Norway |

-
Wetenschap © https://nl.scienceaq.com

