
Wetenschap
Hoe de chaostheorie bemiddelt tussen kwantum- en thermodynamica
1. Gevoeligheid voor initiële omstandigheden:
- De chaostheorie benadrukt het concept van 'gevoelige afhankelijkheid van initiële omstandigheden', ook wel bekend als het vlindereffect. Dit betekent dat kleine veranderingen in de beginvoorwaarden van een chaotisch systeem in de loop van de tijd tot drastisch verschillende uitkomsten kunnen leiden.
- In de kwantummechanica wordt deze gevoeligheid weerspiegeld in de golffunctie van een deeltje, die informatie geeft over de waarschijnlijkheid dat het deeltje in verschillende toestanden wordt aangetroffen. Kleine veranderingen in de golffunctie, zoals faseverschuivingen of verstoringen, kunnen het gedrag van het deeltje aanzienlijk veranderen.
- Op dezelfde manier kunnen in de thermodynamica kleine fluctuaties in temperatuur, druk of andere parameters een aanzienlijke impact hebben op de macroscopische eigenschappen en het gedrag van een systeem.
2. Ergodiciteit en vermenging:
- Ergodiciteit is een fundamentele eigenschap van chaotische systemen, die stelt dat het systeem in de loop van de tijd alle toegankelijke staten met gelijke waarschijnlijkheid bezoekt.
- In de kwantummechanica is ergodiciteit gerelateerd aan het concept van kwantumchaos, waarbij bepaalde kwantumsystemen chaotisch gedrag vertonen vanwege hun gecompliceerde energiespectra en golffuncties. Dit chaotische gedrag kan leiden tot ergodische eigenschappen, zoals een uniforme verdeling van energieniveaus.
- In de thermodynamica suggereert de ergodische hypothese dat een systeem, als het voldoende tijd krijgt, al zijn toegankelijke microtoestanden zal verkennen, wat tot thermisch evenwicht zal leiden.
3. Fractals en vreemde aantrekkende factoren:
- De chaostheorie onthult vaak ingewikkelde patronen die bekend staan als fractals:complexe op zichzelf lijkende structuren die de eigenschap van schaalinvariantie vertonen.
- Fractals zijn gevonden in kwantumsystemen, zoals de energiespectra van bepaalde chaotische kwantumbiljarts of wanordelijke materialen, waar kwantuminterferentie aanleiding geeft tot fractale patronen.
- In de thermodynamica zijn fractals waargenomen in faseovergangen en kritische verschijnselen, zoals de fractale patronen gevormd door bepaalde Ising-modellen of bijna kritische punten.
4. Lyapunov-exponenten:
- Lyapunov-exponenten kwantificeren de mate van divergentie van nabijgelegen trajecten in een chaotisch systeem en karakteriseren de exponentiële groei van kleine verstoringen. Positieve Lyapunov-exponenten duiden op chaotisch gedrag.
- Kwantumchaos kan worden gekarakteriseerd door het berekenen van de kwantum Lyapunov-exponenten, die de groei van de onzekerheid in kwantumgolffuncties in de loop van de tijd meten. Deze exponenten geven inzicht in de mate van kwantumchaos in een bepaald systeem.
- In de thermodynamica worden Lyapunov-exponenten gebruikt om het chaotische gedrag van bepaalde niet-evenwichtssystemen te onderzoeken, zoals turbulente stromingen of faseovergangen die ver van evenwicht zijn.
Door een gemeenschappelijk raamwerk te bieden voor het begrijpen van complex en onregelmatig gedrag, legt de chaostheorie verbanden tussen de kwantummechanica en de thermodynamica. Het laat zien hoe ogenschijnlijk niet-gerelateerde verschijnselen in deze twee domeinen vergelijkbare eigenschappen kunnen vertonen, zoals gevoeligheid voor initiële omstandigheden, ergodiciteit, fractals en Lyapunov-exponenten. Deze verbindingen verdiepen ons begrip van de fundamentele principes die zowel het kwantumrijk als de macroscopische wereld van de thermodynamica beheersen.
Hoofdlijnen
- S-fase: wat gebeurt er tijdens deze subfase van de celcyclus?
- Gedeeltelijk skelet van een voorheen onbekende middelgrote theropode dinosaurus gevonden in Siberië
- Kill-schakelaars voor gemanipuleerde microben die schurkenstaten zijn geworden
- Vogelweervrienden:studenten uit Arkansas printen 3-D eendenpoot
- Voors en tegens van Recombinant DNA Technology
- Multiresistente genetische factoren bij malariaparasieten
- Wat is TA Cloning?
- Hoe vrouwelijke hyena's de mannetjes gingen domineren
- Mogelijk is er een nieuwe biologieregel aan het licht gekomen, die het inzicht in evolutie en veroudering vergroot
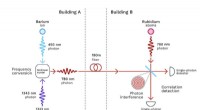
- Wetenschappers correleren fotonparen van verschillende kleuren die in afzonderlijke gebouwen zijn gegenereerd
- Een pad banen voor begraven bits in kwantumchips

- Stephen Hawkings Ph.D. thesis heeft zijn hostwebsite gecrasht - dit is wat het zegt in eenvoudige bewoordingen

- Nieuwe methode zorgt voor snelle, nauwkeurige meting van kwantumtoestanden

- Onderzoekers creëren krachtige kwantumbron met meta-lens-array

 Zijn er waarschuwingssignalen voordat een stofstorm optreedt?
Zijn er waarschuwingssignalen voordat een stofstorm optreedt?  Een strategie om efficiëntere perovskietfilms met smalle bandgap (NBG) te maken voor tandemzonnecellen
Een strategie om efficiëntere perovskietfilms met smalle bandgap (NBG) te maken voor tandemzonnecellen Ironie is het nieuwe zwart
Ironie is het nieuwe zwart IBM-computer blijkt formidabel tegen twee menselijke debaters
IBM-computer blijkt formidabel tegen twee menselijke debaters Stamcellen in bot veranderen met nanoklei-versterkte hydrogel
Stamcellen in bot veranderen met nanoklei-versterkte hydrogel Feds nemen Backpage.com in beslag, websites in handhavingsactie
Feds nemen Backpage.com in beslag, websites in handhavingsactie Eerste directe seismische metingen van Mars onthullen een geologisch actieve planeet
Eerste directe seismische metingen van Mars onthullen een geologisch actieve planeet Hoe reproduceren bacteriën?
Hoe reproduceren bacteriën?
- Elektronica
- Biologie
- Zonsverduistering
- Wiskunde
- French | Italian | Spanish | Portuguese | Swedish | German | Dutch | Danish | Norway |

-
Wetenschap © https://nl.scienceaq.com


