
Wetenschap
Het volgen van de geschiedenis van perturbatieve expansie in de kwantumveldentheorie
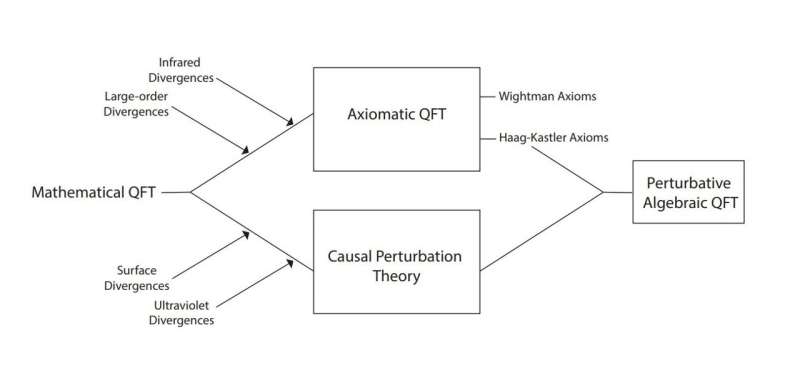
Perturbatieve expansie is een waardevolle wiskundige techniek die op grote schaal wordt gebruikt om beschrijvingen van complexe kwantumsystemen op te splitsen in eenvoudigere, beter beheersbare delen. Misschien wel het allerbelangrijkste is dat het de ontwikkeling van de kwantumveldentheorie (QFT) mogelijk heeft gemaakt:een theoretisch raamwerk dat principes uit de klassieke, kwantum- en relativistische natuurkunde combineert, en dat als basis dient voor het standaardmodel van de deeltjesfysica.
Maar ondanks het belang ervan bij het vormgeven van ons begrip van het universum, wordt de rol van verstorende expansie vaak onderschat bij de bespreking van de wiskundige en filosofische grondslagen van QFT. Door middel van een nieuwe analyse, gepubliceerd in EPJ H, brengt James Fraser van de Universiteit van Wuppertal, samen met Kasia Rejzner van de Universiteit van York, de speciale status van perturbatieve expansies scherper in beeld, door hun diepgewortelde relatie met de fundamenten van QFT te benadrukken.
De bevindingen zijn gepubliceerd in The European Physical Journal H .
In de fundamentele natuurkunde wordt perturbatieve expansie op grote schaal gebruikt om nauwkeurige experimentele voorspellingen uit QFT te halen, die de theorie tot zijn huidige vorm hebben gevormd. Toch worden de vereenvoudigde beschrijvingen die de techniek biedt algemeen gezien als irrelevant bij de bespreking van het wiskundige en filosofische raamwerk van de theorie.
Fraser en Rejzner beweren daarentegen dat de wiskunde van perturbatieve expansie een centrale rol heeft gespeeld in de ontwikkeling van QFT:vaak rechtstreeks in contact met de fundamentele wiskundige structuur ervan. Daarom kan het belang ervan niet worden onderschat bij het bespreken van de fundamentele aard van het universum via QFT.
Via hun paper brengt het duo de geschiedenis van deze relatie scherper in beeld; het traceren van de geschiedenis van het gebruik van perturbatieve expansie in fundamentele ontwikkelingen in QFT. Hun werk zou natuurkundigen uiteindelijk kunnen helpen een dieper inzicht te krijgen in de implicaties van theorieën die zij hebben ontwikkeld met behulp van perturbatieve expansie.