
Wetenschap
Als gebogen materialen plat worden, kan een eenvoudige geometrie de rimpelpatronen voorspellen die ontstaan
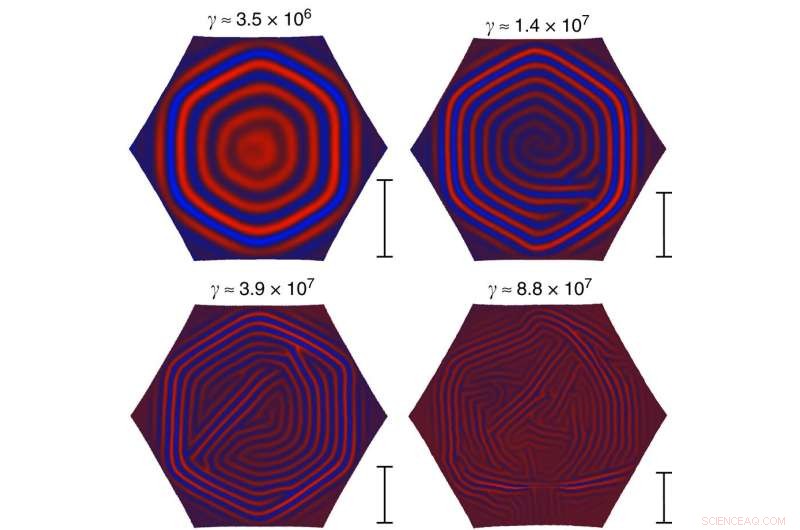
Schalen van domeingrootte. Typische evenwichtsrimpelpatronen in een zeshoekig gedeelte van een dunne bolvormige schaal op een vloeibaar substraat. Alle simulatieparameters blijven vast, behalve de plaatdikte. Het Föppl-von Kármán-getal γ van het systeem wordt boven elk patroon aangegeven. Hoewel het patroon linksboven duidelijk in zes domeinen is verdeeld, lijkt het verhogen van γ de typische domeingrootte te verkleinen. De schaalbalk rechts van elk patroon toont de schaling van typische domeingroottes voorspeld door vergelijking (20), tot een constante factor (alleen de verhoudingen tussen staven zijn zinvol aangezien vergelijking (20) alleen de schaling van de typische grootte en laat de prefactor onbekend). Krediet:Natuurcommunicatie (2017). DOI:10.1038/ncomms15809
Een object dat intrinsiek vlak is, bijvoorbeeld een stuk papier, kan in een cilinder worden gevormd zonder het uit te rekken of te scheuren. Hetzelfde geldt echter niet voor iets dat intrinsiek gebogen is, zoals een contactlens. Wanneer ze worden samengedrukt tussen twee vlakke oppervlakken of op water worden gelegd, worden gebogen objecten plat, maar met rimpels die zich vormen als ze knikken.
Nu heeft onderzoek van de University of Pennsylvania, de University of Illinois Chicago (UIC) en de Syracuse University aangetoond dat het met een eenvoudige geometrie mogelijk is om de patronen van die rimpels te voorspellen, zowel waar ze zich zullen vormen als in sommige gevallen hun richting. De bevindingen, gepubliceerd in Nature Physics , hebben een reeks implicaties, van hoe materialen omgaan met vocht en zonlicht in de natuur weerkaatsen tot de manier waarop een flexibele elektronica kan buigen.
"Het mooie van dit werk is hoe eenvoudig het eigenlijk is", zegt Eleni Katifori, universitair hoofddocent bij Penn's Department of Physics &Astronomy. "Wat erachter zit is erg ingewikkeld, de natuurkunde die door deze regels is vertaald hebben we gevonden, maar de regels zelf zijn heel eenvoudig. Het is inspirerend."
Meeting of the minds
Sinds haar Ph.D. werk, was Katifori geïnteresseerd in de mechanica van hoe dunne membranen krommen. Hoewel dit een curiositeit bleef, draaide haar onderzoekspad in plaats daarvan naar vloeistofstroomnetwerken. Toen Katifori samenwerkte aan een project met Penn-collega Randall Kamien en vervolgens postdoctoraal medestudent Hillel Aharoni, merkte Katifori iets op dat ze op dat moment niet kon verklaren. "Dat wil zeggen, we hebben de rimpels in domeinen opgemerkt", zegt ze.
Met andere woorden, wanneer een gebogen oppervlak wordt afgevlakt, eindigt het met overtollig materiaal en daaropvolgende rimpels. Die rimpels ontstaan in patronen of sectoren. "De vraag werd, waarom zijn de rimpels op die manier gerangschikt?" zegt Katifori. "We begrepen niet hoe belangrijk de domeinen in de rimpels werkelijk zijn."
Op een conferentie in 2016 hoorde wiskundige Ian Tobasco, een assistent-professor bij UIC, Aharoni een lezing geven over het onderwerp. "Het was de eerste keer dat ik dit modelsysteem zag gepresenteerd", zegt Tobasco. "Ik vond het echt cool." Medio 2017 publiceerden Katifori, Aharoni en collega's bevindingen over dit onderwerp in Nature Communications , en later dat jaar ontmoette Tobasco tijdens een workshop Joseph Paulsen uit Syracuse, die voorlopige gegevens had gepresenteerd over de experimenten die zijn groep had gedaan met rimpels.
Begin 2018 begon Tobasco serieus te werken aan een wiskundige theorie voor rimpels, en tijdens de lunch op een conferentie die zomer waren Katifori, Tobasco en Paulsen het erover eens dat ze interesse hadden in dit probleem. Ze besloten samen te werken, met de nadruk op het analyseren van hoeveel de fysieke vorm van het materiaal en de kromming van waaruit het begint, van belang kan zijn voor de rimpelpatronen.
Het probleem oplossen
Voor sommige achtergronden kan kromming positief zijn, zoals de ronding van een honkbal of een wereldbol, of negatief, zoals een paardenzadel of de plek op een glazen fles waar de nek de basis raakt. Er is ook plat materiaal, zoals een stuk papier.
In dit werk concentreerden de onderzoekers zich op positief en negatief gekromde schelpen.
Van elk verwijderden ze vervolgens basisvormen, zoals driehoeken, vierkanten en ovalen. "Denk aan een koekjesvormer. Laten we zeggen dat ik een object met een positieve of negatieve kromming neem, dan knip ik een van deze vormen uit en leg het op vloeistof", zegt Katifori. Zou het mogelijk zijn om de rimpelpatronen te raden en de richting te berekenen waarin de rimpels zouden vloeien? Voor elke vorm loste Tobasco de theorie op op basis van de fundamentele principes die hij had uitgewerkt en gepubliceerd, en kwam vervolgens met voorspellingen.
Op basis van die bevindingen voerden Katifori en Penn, postdoctoraal onderzoeker Desislava Todorova, simulaties uit, waarbij ze individuele vormen en parameters in een computerprogramma invoerden. Soortgelijk werk vond plaats in het laboratorium van Paulsen, een assistent-professor natuurkunde in Syracuse, door middel van experimenten die hij uitvoerde op polystyreenfilm die 1000 keer dunner is dan een stuk papier. "Het is gemaakt van hetzelfde materiaal als het verpakken van pinda's," zegt Tobasco, "maar stel je in plaats van de driedimensionale vorm van een verpakkingspinda voor dat het zo plat is als een vel."
Door de simulaties, experimenten en veel heen en weer om het proces te verfijnen en de oorspronkelijke theorie uit te breiden, begon het trio te onderscheiden dat door het toepassen van eenvoudige geometrische principes, ze van tevoren konden weten welk patroon de rimpels zouden aannemen en voor een subset -wat ze omschrijven als "geordende" rimpels - in welke richting ze zouden rennen.
De geometrische principes
Om een dergelijk principe uit te leggen, gebruikt Katifori een vijfzijdige veelhoek. "Eerst schrijf ik een cirkel in de veelhoek", zegt ze. "De punten waar die cirkel de randen van de veelhoek raakt, bepalen waar ik mijn lijnen trek." Ze pauzeert om een tweede vorm in de eerste te creëren, deze met vier ongelijke kanten; ze begint elke lijn waar de cirkel en de buitenste veelhoek samenkomen en verbindt alle vier de binnenste lijnen. "Nu heb ik een, twee, drie, vier, vijf domeinen", vervolgt ze, wijzend op het kwintet van nieuw afgesloten secties.
Voor eenvoudige vormen zoals deze zullen de buitenste secties geordende rimpels bevatten, die georganiseerd en geordend zijn, in de richting van de binnenste lijnen die Katifori tekende. Binnen de nieuwe binnenste veelhoek vormen zich nog steeds rimpels, maar ze blijven ongeordend en onvoorspelbaar.
Tobasco wijst op een ander voorbeeld, waarvan hij vaststelde dat het universeel waar was voor vormen gesneden uit negatief gebogen schelpen. "Uiteindelijk is het heel eenvoudig om de rimpelpatronen te voorspellen. Je hoeft alleen maar lijnsegmenten te tekenen die de grens in een rechte hoek raken." Met andere woorden, begin op een punt binnen de vorm en maak een directe lijn naar de rand van de vorm, maar alleen op een plek waar dan een rechte hoek ontstaat.
Dat duurde een jaar voordat het team het begreep. "De vergelijkingen die de lay-out van rimpels bepalen, zijn verschrikkelijk om op te lossen, en veel van de patronen die we in onze experimenten en simulaties hebben waargenomen, zijn behoorlijk gecompliceerd", zegt Paulsen. "Maar het blijkt dat je onder bepaalde omstandigheden de kreuklay-out kunt voorspellen met een simpele set regels. Dat betekent dat we nu een snelle, efficiënte manier hebben om kreukpatronen te ontwerpen."
"De eenvoud is mooi en het is ook nuttig", voegt hij eraan toe, vooral voor gerimpelde oppervlakken die een functie hebben zoals het mogelijk maken van hechting of vloeistofstroom.
Katifori noemt soortgelijke voorbeelden. "Laten we zeggen dat er vocht of vocht in de lucht is. Water zal zich anders gedragen in de valleien en de heuvels van een gegroefd oppervlak", zegt ze. "Door het rimpelpatroon onder controle te houden, kun je misschien beïnvloeden hoe het water condenseert."
Wat daarna komt
De onderzoekers moeten nog meer begrijpen over deze complexe getextureerde oppervlakken, zoals hoe patronen te trekken uit ongeordende rimpels, waarom geordende en ongeordende domeinen naast elkaar kunnen bestaan, en waarom er een "wederkerigheid" is die negatief en positief gebogen schelpen verbindt, wat betekent dat zodra het patroon voor één is bepaald, is het eenvoudig om het patroon voor de ander te voorspellen.
Voor nu zeggen ze echter dat ze enthousiast zijn over het potentieel van wat ze tot nu toe hebben geleerd.
"Je hebt een ingewikkelde theorie die uiteindelijk neerkomt op relatief eenvoudige wiskunde die bijna iedereen kan doen met een kompas en een liniaal", zegt Katifori. "Het is een elegante en mooie oplossing voor een complex probleem." + Verder verkennen
Wiskundige bewijzen, experimenten en simulaties gebruiken om te laten zien hoe een materiaal kreukt wanneer het wordt platgedrukt
 Simulatie op atoomschaal van antiaritmische geneesmiddelinteractie met hartcellen
Simulatie op atoomschaal van antiaritmische geneesmiddelinteractie met hartcellen Onderzoekers kunnen nu snel nauwkeurig scannen op nutriëntengehalte in het gangpad met producten
Onderzoekers kunnen nu snel nauwkeurig scannen op nutriëntengehalte in het gangpad met producten Lab-gekweekte pigmenten en voedselbijproducten:de toekomst van natuurlijke textielkleurstoffen
Lab-gekweekte pigmenten en voedselbijproducten:de toekomst van natuurlijke textielkleurstoffen Nieuwe aanpak bepaalt optimale materiaalontwerpen met minimale gegevens
Nieuwe aanpak bepaalt optimale materiaalontwerpen met minimale gegevens Testen van ontworpen koolstofmaterialen om afvalwater te zuiveren
Testen van ontworpen koolstofmaterialen om afvalwater te zuiveren
Hoofdlijnen
- Hoe je geur te verbergen voor honden
- Wat is een andere naam voor somatische stamcellen en wat doen ze?
- Wedstrijden om vrouwelijke aandacht maken van mannen betere presteerders - in fruitvliegjes
- Virus doodt 100.000 runderen in India, bedreigt levensonderhoud
- Waarom zingen mensen onder de douche?
- Lijst met ingekapselde bacteriën
- Anabolisch versus katabolisch (celmetabolisme): definitie en voorbeelden
- Het effect van zonlicht op dieren en planten
- Oorlog verstoort de natuur permanent, studie vondsten
- Onderzoekers bewijzen dat fragmenten van splijtende atoomkernen beginnen te draaien na splitsing

- Doorbraak verbetert enorm de ultrasnelle resolutie die haalbaar is met röntgenvrije-elektronenlasers

- Nieuwe techniek digitaliseert transparante objecten nauwkeurig

- Aerodynamica van neerstrijkende vogels kan het ontwerp van vliegtuigen beïnvloeden

- Ontdekking van topologische LC-circuits die EM-golven transporteren zonder terugverstrooiing

 Kunnen witte dwergen het kosmologische lithiumprobleem helpen oplossen?
Kunnen witte dwergen het kosmologische lithiumprobleem helpen oplossen? Witte grafeenstructuren kunnen de hitte aan
Witte grafeenstructuren kunnen de hitte aan Nanotechnologie-experts creëren eerste optische polarisatieschakelaar met terahertz-snelheid
Nanotechnologie-experts creëren eerste optische polarisatieschakelaar met terahertz-snelheid Hoe werkt een ampèremeter?
Hoe werkt een ampèremeter?  Voors en tegens van een waterverzachter
Voors en tegens van een waterverzachter Miljoenen opgesloten aan verkeerde kant van digitale kloof
Miljoenen opgesloten aan verkeerde kant van digitale kloof Zondebelastingen kunnen anderen onbedoeld laten betalen
Zondebelastingen kunnen anderen onbedoeld laten betalen Satelliet ziet tropische cycloon Titli aan land komen in Noordoost-India
Satelliet ziet tropische cycloon Titli aan land komen in Noordoost-India
- Elektronica
- Biologie
- Zonsverduistering
- Wiskunde
- French | Italian | Spanish | Portuguese | Swedish | German | Dutch | Danish | Norway |

-
Wetenschap © https://nl.scienceaq.com

