
Wetenschap
Topologische bescherming van verstrengeld licht van twee fotonen in fotonische topologische isolatoren
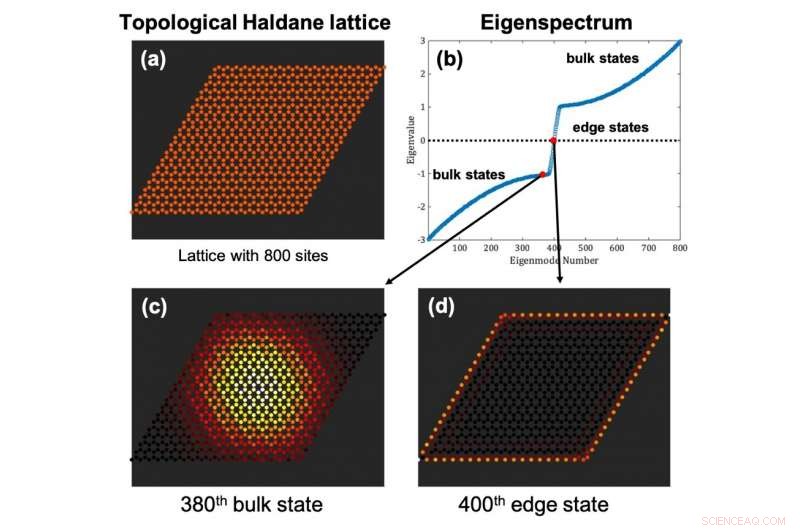
Figuur 1:Topologische isolatoren zijn roostersystemen van eindige grootte (a) die eigenspectra vertonen waarbij (b) de eigenenergieën van bulktoestanden (c) een bandafstand vertonen die (d) de eigenenergieën van zogenaamde randtoestanden bevat. Krediet:MBI/HU
In een gezamenlijke inspanning, onderzoekers van de Humboldt-Universität (Berlijn), het Max Born Institute (Berlijn) en de University of Central Florida (V.S.) hebben de noodzakelijke voorwaarden onthuld voor het robuuste transport van verstrengelde toestanden van twee-fotonlicht in fotonische topologische isolatoren, de weg vrijmaken voor ruisbestendig transport van kwantuminformatie. De resultaten zijn verschenen in Natuur Communicatie.
Oorspronkelijk ontdekt in systemen van gecondenseerde materie, topologische isolatoren zijn tweedimensionale materialen die verstrooiingsvrij (unidirectioneel) transport langs hun randen ondersteunen, zelfs in aanwezigheid van gebreken en wanorde. In essentie, topologische isolatoren zijn eindige roostersystemen waarbij, gegeven een geschikte beëindiging van het onderliggende oneindige rooster, randtoestanden worden gevormd die in een goed gedefinieerde energiekloof liggen die verband houdt met de bulktoestanden, d.w.z. deze randtoestanden zijn energetisch gescheiden van de bulktoestanden (figuur 1).
belangrijk, randtoestanden van één deeltje in dergelijke systemen zijn topologisch beschermd tegen verstrooiing:ze kunnen zich niet in de bulk verspreiden omdat hun energie in de opening ligt, en ze kunnen niet achterwaarts verstrooien omdat achterwaarts voortplantende randtoestanden ofwel afwezig zijn of niet gekoppeld zijn aan de voorwaarts voortplantende randtoestanden.
De haalbaarheid van het engineeren van complexe Hamiltonianen met behulp van geïntegreerde fotonische roosters in combinatie met de beschikbaarheid van verstrengelde fotonen, verhoogt de intrigerende mogelijkheid om topologisch beschermde verstrengelde toestanden te gebruiken in optische kwantumcomputers en informatieverwerking (Science 362, 568, (2018), optiek 6, 955 (2019)).
Het bereiken van dit doel, echter, is hoogst niet-triviaal, aangezien topologische bescherming zich niet zonder meer uitbreidt tot (terug)verstrooiing van meerdere deeltjes. Aanvankelijk, dit feit lijkt contra-intuïtief te zijn omdat individueel, elk deeltje wordt beschermd door topologie, terwijl gezamenlijk, verstrengelde (gecorreleerde) deeltjes worden zeer gevoelig voor verstoringen van het ideale rooster. Het onderliggende fysieke principe achter deze schijnbare discrepantie is dat, kwantum mechanisch, identieke deeltjes worden beschreven door toestanden die voldoen aan een principe van uitwisselingssymmetrie.
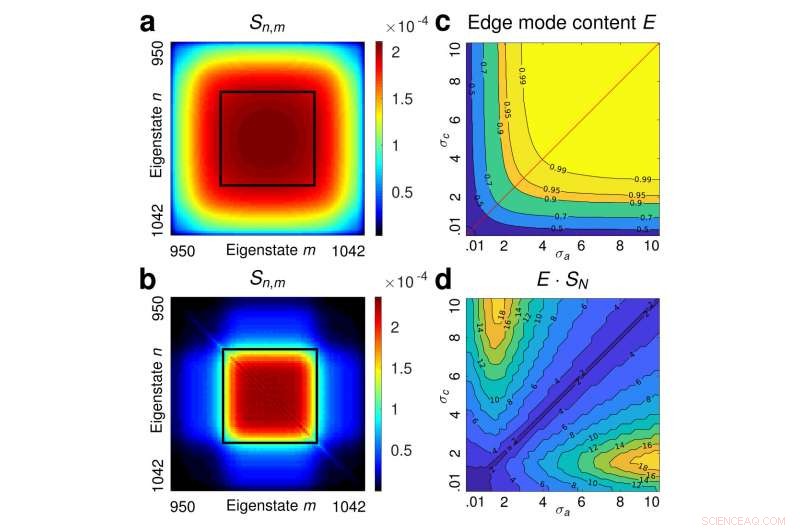
Figuur 2:Om het topologische beschermingsvenster te identificeren, de onderzoekers beschouwden een spectraal brede producttoestand als begintoestand en propageren deze door een ensemble van 1000 willekeurige Haldane-roosters. (a) Toont de spectrale correlatiekaart voor de begintoestand en in (b) het ensemble-gemiddelde van de spectrale correlatiekaarten binnen de edge-edge subruimte nadat de voortplanting door het ensemble van ongeordende roosters wordt getoond. Het is gebleken dat de enige amplitudes van twee fotonen die de verstrooiing die door de stoornis wordt veroorzaakt, overleven, in het gebied liggen dat wordt aangegeven door het zwarte vierkant dat het beschermingsvenster is. Eindelijk, (c) en (d) weergave, respectievelijk, de edge-mode content E en het product van de edge-mode content met het Schmidt-getal E · SN als functie van de varianties van de begintoestanden. Krediet:MBI/HU
In hun werk, de onderzoekers boeken verschillende fundamentele vooruitgang in het begrijpen en beheersen van topologische bescherming in de context van toestanden met meerdere deeltjes:
- Eerst, ze identificeren fysieke mechanismen die een kwetsbaarheid van verstrengelde toestanden in topologische fotonische roosters veroorzaken en presenteren duidelijke richtlijnen voor het maximaliseren van verstrengeling zonder topologische bescherming op te offeren.
- Tweede, ze vestigen en demonstreren een drempelachtig gedrag van verstrengelingskwetsbaarheid en identificeren voorwaarden voor robuuste bescherming van sterk verstrengelde twee-fotontoestanden.
Precies zijn, ze onderzoeken de impact van wanorde op een reeks van twee-fotontoestanden die zich uitstrekken van de volledig gecorreleerde tot de volledig anti-gecorreleerde limieten, waardoor ook een volledig scheidbare staat wordt gedekt. Voor hun analyse ze beschouwen twee topologische roosters, een periodiek en een aperiodiek. In het periodieke geval ze beschouwen het Haldane-model, en voor het aperiodieke geval, een vierkant rooster, waarvan de dynamiek van één deeltje overeenkomt met het kwantum Hall-effect, wordt bestudeerd.
De resultaten bieden een duidelijke routekaart voor het genereren van robuuste golfpakketten die zijn afgestemd op de betreffende aandoening. specifiek, ze stellen grenzen aan de stabiliteit van verstrengelde toestanden tot relatief hoge verstrengelingsgraden die praktische richtlijnen bieden voor het genereren van bruikbare verstrengelde toestanden in topologische fotonische systemen. Verder, deze bevindingen tonen aan dat om verstrengeling te maximaliseren zonder topologische bescherming op te offeren, de gezamenlijke spectrale correlatiekaart van twee-fotontoestanden moet passen binnen een goed gedefinieerd topologisch beschermingsvenster. (Figuur 2).
 Formules voor het bepalen van de specifieke zwaartekracht
Formules voor het bepalen van de specifieke zwaartekracht Gegevensherinneringen van morgen:nieuwe technologie gebruiken om magneten met één molecuul in slow motion te verkennen
Gegevensherinneringen van morgen:nieuwe technologie gebruiken om magneten met één molecuul in slow motion te verkennen De waardevolle bijdrage van stress aan de thermische stabiliteit van polykristallijne legeringen met nanokorrels
De waardevolle bijdrage van stress aan de thermische stabiliteit van polykristallijne legeringen met nanokorrels Door de interne structuur van 2D-hybride perovskietmaterialen te wijzigen, zenden ze wit licht uit
Door de interne structuur van 2D-hybride perovskietmaterialen te wijzigen, zenden ze wit licht uit Nieuwe reactie maakt indoline-steigers beschikbaar voor farmaceutische ontwikkeling
Nieuwe reactie maakt indoline-steigers beschikbaar voor farmaceutische ontwikkeling
 Griekse megabranden wijzen op mislukking in voorbereiding deskundigen zeggen
Griekse megabranden wijzen op mislukking in voorbereiding deskundigen zeggen Staat de Brunt-ijsplaat op de rand?
Staat de Brunt-ijsplaat op de rand? Supertyfoon Tramis-regenval onderzocht door NASA / JAXAs GPM-satelliet
Supertyfoon Tramis-regenval onderzocht door NASA / JAXAs GPM-satelliet Langetermijnmetingen laten zien hoe het klimaat verandert
Langetermijnmetingen laten zien hoe het klimaat verandert Genomische gegevens vangen koralen op bij soortvorming en aanpassing
Genomische gegevens vangen koralen op bij soortvorming en aanpassing
Hoofdlijnen
- Rechtbank vindt het goed om een soort uil te doden om het effect op andere uilen te zien
- Hoe stadia van mitose in een cel onder een microscoop te identificeren
- Celmodel onthult dynamische aard van segmentatieklok die de vorming van wervels stimuleert
- Bestorming van het kasteel:nieuwe ontdekking in de strijd tegen bacteriën
- Graafwespen en hun chemie
- Ingewikkelde ijsgrotten in Antarctica May Harbor Unique Life
- Iberische bruine beren stammen niet af van degenen die tijdens de ijstijd uit het noorden zijn gevlucht
- Het korstmos dat zijn voortplantingsstrategie verandert afhankelijk van het klimaat
- Het belang van asymmetrie bij bacteriën
- Welke materialen dragen de beste geluidsgolven?

- Razendsnelle algoritmen kunnen de belasting van het genereren van 3D-hologrammen verlichten
- Stijgt een ballon met helium hoger dan één met zuurstof?

- Onderzoekers gebruiken infrarood licht om moleculen te detecteren

- Eerste natuurkundige resultaten van prototype detector gepubliceerd

 Recente trends in de opwarming van de aarde zijn niet in overeenstemming met een zeer hoge klimaatgevoeligheid
Recente trends in de opwarming van de aarde zijn niet in overeenstemming met een zeer hoge klimaatgevoeligheid Het begraven van koolstof kan de koolstofvastlegging verbeteren zonder de grasproductiviteit te verminderen
Het begraven van koolstof kan de koolstofvastlegging verbeteren zonder de grasproductiviteit te verminderen Mensen zouden in vulkanische tunnels op de maan kunnen leven
Mensen zouden in vulkanische tunnels op de maan kunnen leven Een graslandecosysteemproject in een schoenendoos doen
Een graslandecosysteemproject in een schoenendoos doen Uber koopt Midden-Oosten rivaal Careem:rapport
Uber koopt Midden-Oosten rivaal Careem:rapport Tencent-investering in Reddit wekt censuurzorg op
Tencent-investering in Reddit wekt censuurzorg op Hoe aaseters forensische wetenschappers kunnen helpen bij het identificeren van menselijke lijken
Hoe aaseters forensische wetenschappers kunnen helpen bij het identificeren van menselijke lijken Waar voedsel beperkt is, guppy-moeders dragen hun jongen langer
Waar voedsel beperkt is, guppy-moeders dragen hun jongen langer
- Elektronica
- Biologie
- Zonsverduistering
- Wiskunde
- French | Italian | Spanish | Portuguese | Swedish | German | Dutch | Danish | Norway |

-
Wetenschap © https://nl.scienceaq.com

