
Wetenschap
Games spelen met kwantuminterferentie
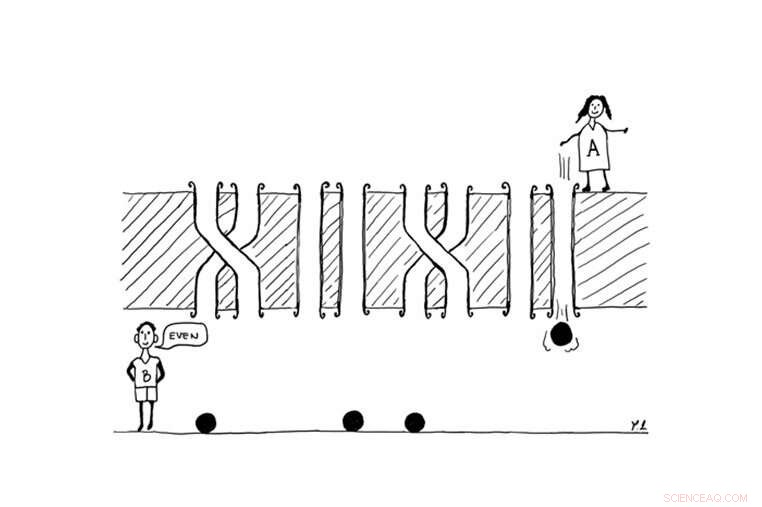
De figuur toont het eenvoudigste voorbeeld van pariteitsspellen. Alice (A) gooit een bepaald aantal knikkers naar Bob (B), met als doel te leren of het aantal getwiste buizen even of oneven is. De spelers hebben vier gewone klassieke knikkers nodig om de taak te voltooien. In tegenstelling tot, al zouden twee kwantumknikkers voldoende zijn. Krediet:© Borivoje Dakić
Zoals Richard Feynman het zei:"het dubbelspletenexperiment is absoluut onmogelijk op een klassieke manier uit te leggen en heeft het hart van de kwantummechanica in zich. In werkelijkheid, het bevat het enige mysterie."
Inderdaad, bij dit experiment, een kwantumdeeltje gedraagt zich alsof het zich tegelijkertijd op twee verschillende locaties bevindt, en vertoont paradigmatische golfachtige verschijnselen zoals interferentie. Echter, later werd opgemerkt dat experimenten met meerdere sleuven aantonen dat de mate van delokalisatie van kwantumdeeltjes zijn grenzen heeft, en dat in zekere zin kwantumdeeltjes kunnen niet tegelijkertijd op meer dan twee locaties worden gedelokaliseerd. Deze beperking heeft een puzzel gecreëerd die tot op de dag van vandaag nog niet helemaal is opgelost. Onderzoekers van de Universiteit van Wenen en IQOQI-Vienna (Oostenrijkse Academie van Wetenschappen) hebben een belangrijke stap gezet om dit probleem te begrijpen door interferentie-experimenten te herformuleren in termen van informatie-theoretische spellen. Hun analyse, die onlangs is verschenen in het tijdschrift Quantum, biedt een intuïtieve manier van denken over interferentieverschijnselen en de beperkingen ervan, daarmee de weg vrijmakend voor het oplossen van de bovengenoemde puzzel.
Een van de meest opvallende kenmerken van de kwantummechanica is het superpositieprincipe. Dit principe kan het gemakkelijkst worden geïllustreerd via het dubbelspletenexperiment, waarbij een deeltje wordt gestuurd dat door een plaat wordt gestuurd die is doorboord met twee spleten. Volgens onze alledaagse intuïties, men zou kunnen verwachten dat het deeltje altijd door één spleet gaat, of via de andere. Echter, kwantummechanica houdt in dat het deeltje in zekere zin door beide spleten tegelijk kan gaan, dat is, het kan zich tegelijkertijd in een superpositie van twee locaties bevinden. Deze mogelijkheid ligt ten grondslag aan het fenomeen van kwantuminterferentie, d.w.z. het opvallende golfachtige gedrag van kwantumdeeltjes. Nutsvoorzieningen, is er een manier om de mate te kwantificeren waarin kwantumdeeltjes kunnen worden gedelokaliseerd? Staat de kwantumtheorie toe dat deeltjes meer dan twee paden tegelijk afleggen? Om deze vragen te begrijpen, natuurkundigen hebben "multi-slit experimenten, ", die alleen verschillen van het experiment met dubbele spleten in het aantal spleten:bijvoorbeeld een experiment met drie spleten omvat een deeltje dat door drie spleten wordt gestuurd.
Je zou kunnen denken dat als een kwantumdeeltje tegelijkertijd door twee spleten kan gaan, het moet ook in staat zijn om tegelijkertijd door drie, vier, of een willekeurig aantal spleten. Verrassend genoeg, er werd onmiddellijk opgemerkt dat elk patroon verkregen in experimenten met meerdere spleten kan worden verklaard doordat het deeltje altijd door maximaal twee spleten tegelijk gaat. Hoewel deze functie wiskundig volledig wordt begrepen, de volgende vragen blijven onbeantwoord:is er een fysieke reden voor de schijnbare asymmetrie tussen het dubbelspletenexperiment en het meerspletenexperiment? Wat ligt ten grondslag aan deze enigszins willekeurige beperking van de "delokalisatie" van kwantumdeeltjes?
In hun recente werk Sebastian Horvat en Borivoje Dakić, onderzoekers van de Universiteit van Wenen en IQOQI-Vienna (Oostenrijkse Academie van Wetenschappen), hebben een belangrijke stap gezet om dit probleem te begrijpen door het aan te pakken met informatietheorie. Namelijk, ze hebben interferentieverschijnselen en experimenten met meerdere sleuven geherformuleerd in termen van "pariteitsspellen", waarvan het eenvoudigste voorbeeld wordt geïllustreerd in de figuur. Het spel bestaat uit twee spelers, Alice en Bob, die worden gescheiden door een muur die is doorboord met vier paar buizen. Elk paar buizen kan recht of gedraaid zijn, en het aantal getwiste paren is zowel Alice als Bob niet bekend. Verder, Alice heeft een bepaald aantal knikkers tot haar beschikking die ze door de buizen naar Bob kan schieten; de spelers kunnen deze knikkers gebruiken om iets te leren over de structuur van de buizen.
Het doel van het spel is dat de spelers samenwerken en uitzoeken of het totale aantal getwiste paren even of oneven is, door zo min mogelijk knikkers te gebruiken. Nutsvoorzieningen, stel dat Alice een knikker door een van de buizen gooit, bijvoorbeeld via de tweede. Bob kan dan gemakkelijk afleiden of het eerste paar buizen recht of gedraaid is door simpelweg te controleren of de knikker door de tweede buis of door de eerste is gevallen. analoog, als Alice vier knikkers tot haar beschikking heeft, ze kan ze allemaal door de rechterbuis van elk paar flitsen (zoals het geval is in de afbeelding). Bob kan dan eenvoudig het aantal getwiste paren afleiden, en dus of dit aantal even of oneven is, daarmee het spel te winnen. Echter, als het aantal buizenparen groter is dan het aantal knikkers dat Alice tot haar beschikking heeft, dan kan het spel niet worden gewonnen, aangezien er altijd ten minste één paar buizen zal zijn, waarover Bob geen enkele informatie kan verzamelen. Daarom, om het spel te winnen, de spelers moeten zoveel knikkers gebruiken als er paren buizen zijn.
Anderzijds, kwantummechanica, en meer specifiek, het superpositieprincipe, stelt de spelers in staat om het spel te winnen dat in de afbeelding wordt geïllustreerd door slechts twee "kwantumknikkers" te gebruiken! Een manier om te begrijpen waar deze verbetering vandaan komt, is door te onthouden, zoals eerder vermeld, dat een kwantumdeeltje "tegelijkertijd door twee locaties kan gaan". Twee kwantumknikkers kunnen dus "tegelijkertijd door vier locaties gaan", waarbij het gedrag van vier gewone (klassieke) knikkers wordt nagebootst. "In dit spel, knikkers gedragen zich analoog aan lopers die door de buizen kunnen worden gestoken. Wanneer Alice een gewone klassieke knikker plaatst, het is alsof ze 1 cent heeft gestoken.
Anderzijds, aangezien de kwantumtheorie knikkers toestaat om "tegelijkertijd door 2 buizen te gaan", elke kwantummarmer is 2 cent waard. De waarde van de tokens is additief:bijvoorbeeld om het spel te winnen, Alice kan 4 klassieke knikkers of 2 kwantumknikkers plaatsen, aangezien de totale tokenwaarde in beide gevallen gelijk is aan 4 penningen", legt Sebastian Horvat uit. Anderzijds, Bedenk dat een kwantumdeeltje niet door meer dan twee locaties tegelijk kan gaan:dit wordt weerspiegeld in het feit dat Alice en Bob het spel niet kunnen winnen door minder dan twee kwantumknikkers te gebruiken. Vandaar, om het spel te winnen, het aantal kwantumknikkers dat door Alice wordt verzonden, moet gelijk zijn aan ten minste de helft van het totale aantal buizenparen.
In hun werk, de onderzoekers hebben meer algemene formuleringen van dit spel geanalyseerd en de prestaties van de spelers bestudeerd, afhankelijk van het aantal deeltjes en of de deeltjes klassiek zijn, quantum, of van meer algemene en hypothetische aard. Borivoje Dakić voegt toe:"Deze hypothetische deeltjes hebben een hogere informatieverwerkingskracht, dat is, hun corresponderende tokens zijn meer dan 2 cent geldig. Het is niet duidelijk waarom de natuur de voorkeur zou geven aan klassieke en kwantumdeeltjes boven deze hypothetische:dit is iets dat we in de toekomst nog moeten bestuderen."
Globaal genomen, pariteitsspellen bieden een alternatieve beschrijving van kwantuminterferentie binnen een meer algemeen en intuïtief kader, die hopelijk licht werpen op nieuwe kenmerken van kwantumsuperpositie, vergelijkbaar met hoe de studie van kwantumverstrengeling is verdiept door de formulering van de zogenaamde 'niet-lokale spellen'.
Hoofdlijnen
- Waar bevindt het DNA zich in een cel?
- Wat doet de DNA-nucleotide volgorde code voor?
- Door het bedrijf gesponsorde klinische CRISPR-onderzoeken starten in 2018
- Hoe afnemende zoogdierpopulaties in de Florida Everglades verband houden met de invasieve Birmese python
- Wat is een gespecialiseerd gebied van het endoplasmatisch reticulum?
- Beschrijving van de basisfuncties van enzymen in cellen
- Verschillende soorten enzymen
- De primaire primaire productiviteit berekenen
- Wat is de rol van enzymen in het metabolisme?
- Een nieuwe benadering voor het bestuderen van elektrische ladingsarrangementen in een supergeleider

- Voordelen en nadelen van plastic tandwielen

- Hoe bouw je een sterk en stabiel structuurproject voor school

- Hoeveel gewicht neemt een katrol op?

- Chiraal Faraday-effect doorbraak, dankzij helices van nikkel

 Verbod op sociale media, beperkingen hebben een gemengd effect op mogelijke verkeerde informatie na rellen in het Capitool
Verbod op sociale media, beperkingen hebben een gemengd effect op mogelijke verkeerde informatie na rellen in het Capitool Tool voor het oogsten van big data zorgt voor slimme landbouw
Tool voor het oogsten van big data zorgt voor slimme landbouw Avogadros-nummer gebruiken om massa te vinden
Avogadros-nummer gebruiken om massa te vinden  Een nieuwe theorie om te verklaren hoe de duinen op Titan zijn gevormd
Een nieuwe theorie om te verklaren hoe de duinen op Titan zijn gevormd Wat is Saturnus Core gemaakt van?
Wat is Saturnus Core gemaakt van?  Zou jij je auto dumpen als het openbaar vervoer gratis zou zijn? Dit is wat onderzoekers hebben gevonden
Zou jij je auto dumpen als het openbaar vervoer gratis zou zijn? Dit is wat onderzoekers hebben gevonden Mythe van de magische blik van Mona Lisa ontkracht
Mythe van de magische blik van Mona Lisa ontkracht AstroSAT-waarnemingen onthullen quasi-periodieke oscillaties in de röntgendubbele GX 5-1
AstroSAT-waarnemingen onthullen quasi-periodieke oscillaties in de röntgendubbele GX 5-1
- Elektronica
- Biologie
- Zonsverduistering
- Wiskunde
- French | Italian | Spanish | Portuguese | Swedish | German | Dutch | Danish | Norway |

-
Wetenschap © https://nl.scienceaq.com


