
Wetenschap
Netwerkisotopie:een raamwerk om de 3D-lay-outs van fysieke netwerken te bestuderen
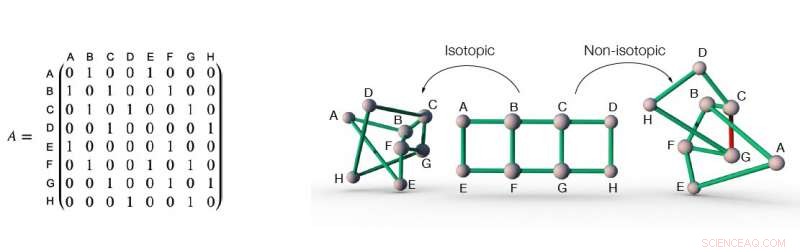
De aangrenzende matrix van een netwerk (links), en drie verschillende inbeddingen van dit netwerk in de ruimte (rechts). De aangrenzende matrix van een netwerk registreert informatie over de connectiviteit van het netwerk. Bijvoorbeeld, in het netwerk in de figuur, knooppunt A en B zijn verbonden door een link, daarom is het element in de aangrenzende matrix op het snijpunt van rij A en kolom B één. evenzo, knooppunt A en C zijn niet verbonden door een link, daarom is het element in de aangrenzende matrix op het snijpunt van rij A en kolom C nul. De eerste twee netwerkinbeddingen van het netwerk beschreven door de aangrenzende matrix aan de linkerkant zijn isotoop ten opzichte van elkaar, omdat ze in elkaar kunnen worden omgezet door simpelweg de inbedding "af te vlakken", zonder de noodzaak om een link open te knippen. Anderzijds, de inbedding aan de rechterkant is niet-isotopisch voor de andere twee inbeddingen, want om het in de andere twee te veranderen, er moet minimaal één link (bijvoorbeeld de rode link) worden opengeknipt om andere link(s) door te laten. Krediet:Liu, Dehmamy &Barabási.
De structuur en functies van veel fysieke netwerken, inclusief het menselijk brein, het vasculaire systeem en andere biologische netwerken, zijn vaak afhankelijk van hun driedimensionale en geometrische lay-out. Onderscheid maken tussen fysieke netwerken met identieke verbindingen maar verschillende geometrische lay-outs, echter, kan heel uitdagend zijn.
Onderzoekers van de Northeastern University hebben onlangs een theoretische constructie geïntroduceerd, netwerkisotopie genaamd, die wetenschappers zou kunnen helpen onderscheid te maken tussen fysieke netwerken. Netwerkisotopie biedt een classificatietool die klassen van 3D-netwerklay-outs schetst die in elkaar kunnen worden getransformeerd zonder verbindingskruisingen.
"Ons project begon als een nieuwsgierigheid naar netwerklay-outs, "Yanchen Liu, een van de onderzoekers die het onderzoek heeft uitgevoerd, vertelde Phys.org. "Er zijn veel 3D-geprinte netwerken in ons kantoor die in verschillende projecten in het lab zijn bestudeerd. Als we naar deze netwerken kijken, we vroegen ons af:als er voor een bepaald netwerk (vaste bedrading van de links) oneindig veel manieren zijn om de knooppunten en links in de 3D-ruimte te plaatsen, hoe kunnen we zien of twee lay-outs van hetzelfde netwerk hetzelfde of verschillend zijn? Bovendien, hoe moeten we de overeenkomsten tussen netwerklay-outs definiëren en als twee lay-outs verschillend zijn, hoe moeten we het verschil tussen hen meten?"
Kort nadat ze begonnen met hun onderzoek, Liu en haar collega's realiseerden zich dat er twee belangrijke manieren zijn waarop geometrische netwerklay-outs van elkaar kunnen verschillen. De eerste hiervan hangt af van de mate waarin de lay-out van een netwerk wordt uitgerekt, terwijl de tweede het resultaat is van zogenaamde link-crossing (d.w.z. links die door elkaar heen gaan).
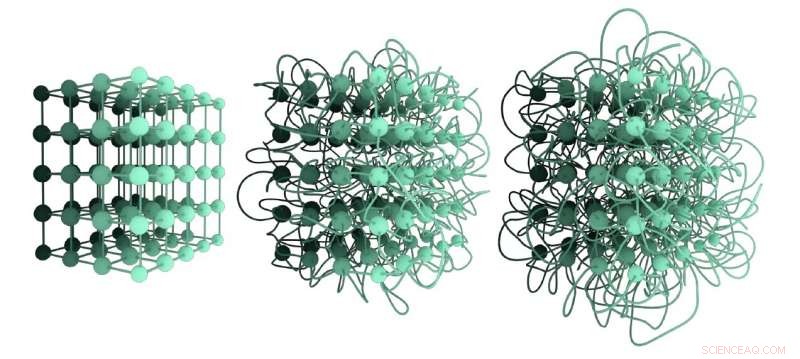
Drie verschillende niet-isotopische inbeddingen van hetzelfde roosternetwerk. De inbedding aan de linkerkant is ontward; de inbedding in het midden is meer verward in vergelijking met de eerste, en de derde inbedding is de meest verwarde. Hun mate van verwarring kan worden gekwantificeerd door het Graph Linking Number. Krediet:Liu, Dehmamy &Barabási.
"Het eerste type verschil is triviaal, maar het tweede type verschil is intrigerend, Liu legde uit. "Vergelijkbare vragen zijn bestudeerd in de knooptheorie, dat is een veld gewijd aan knopen gevormd door een of meer gesloten bochten."
De inbedding van een fysiek netwerk (d.w.z. layout) is in wezen een beschrijving van hoe de knooppunten en koppelingen in de ruimte worden samengevoegd. In hun krant Liu en haar collega's introduceerden een concept genaamd netwerkinbedding isotopie dat kan worden gebruikt om onderscheid te maken tussen verschillende mogelijke inbeddingen van een bepaald netwerk in de 3D-ruimte.
"Als twee netwerkinbeddingen isotoop ten opzichte van elkaar zijn, het betekent dat ze in elkaar kunnen worden uitgerekt zonder een schakel open te snijden om andere schakels door te laten, " zei Liu. "Aan de andere kant, als twee netwerkinbeddingen niet-isotopisch zijn ten opzichte van elkaar, het betekent dat ze nooit continu in elkaar kunnen worden omgezet zonder schakels te verbreken."
Het begrip netwerkisotopie, zoals gedefinieerd door dit team van onderzoekers, kan worden gebruikt om te meten in hoeverre verschillende netwerkinbeddingen verstrengeld zijn, een maat die het grafiekkoppelingsgetal wordt genoemd. interessant, Liu en haar collega's ontdekten dat deze maat ook gecorreleerd is met de elastische energie van een lay-out.
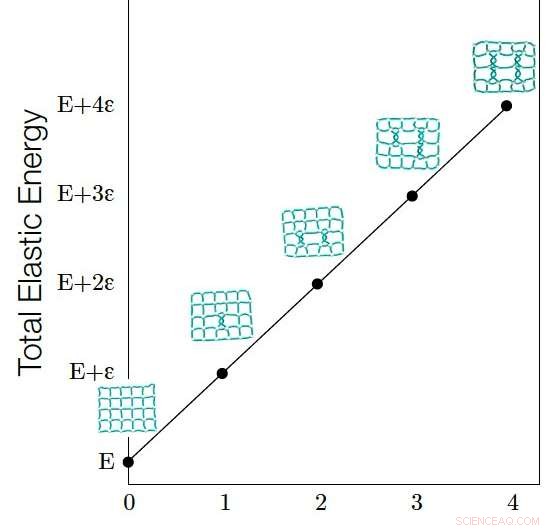
De elastische energie (E) van een netwerkinbedding blijkt lineair gecorreleerd te zijn met het Graph Linking Number (G). De elastische energie van een netwerkinbedding is evenredig met de totale lengte van alle verbindingen. De lineaire relatie tussen E en G kan worden verklaard door het feit dat elke toename in G de schakels in de netwerkinbedding uitrekt, die op zijn beurt E verhoogt, en de hoeveelheid energietoename veroorzaakt door elke tangle (elke tangle zorgt ervoor dat G met één toeneemt) wordt gekwantiseerd en is een constante. Krediet:Liu, Dehmamy &Barabási.
Veel fysieke systemen kunnen worden omschreven als netwerken, een aanzienlijk deel daarvan zijn fysieke netwerken. De door de onderzoekers geïntroduceerde theoretische concepten zijn effectieve hulpmiddelen om de eigenschappen en geometrische kenmerken van deze systemen te bestuderen.
"Er zijn drie belangrijke prestaties in dit document, Naar mijn mening, " zei Liu. "De eerste is dat we netwerkinbedding van isotopie hebben gedefinieerd, wat een uitbreiding is van knoopisotopie van knooptheorie tot netwerkinbeddingen. De tweede is dat we het grafiekkoppelingsnummer hebben uitgevonden, een nuttige maatstaf voor de mate van verwarring van netwerkinbeddingen. Eindelijk, we ontdekten dat het nummer van de graafverbinding van een netwerkinbedding gecorreleerd is met de elastische energie van die netwerkinbedding."
Liu en haar collega's gebruikten hun bevindingen om een statistisch model te ontwikkelen dat de vorming van tangles in een fysiek netwerk beschrijft. In de toekomst, dit model zou kunnen worden gebruikt om te evalueren in hoeverre de 3D-lay-out van een fysiek systeem verstrengeld is.
In hun recente krant bijvoorbeeld, gebruikten de onderzoekers het om de verstrengeling van veel fysieke systemen te onderzoeken, inclusief het muizenbrein. Aangezien alle theoretische constructies die in dit artikel worden geïntroduceerd, kunnen worden toegepast op een breed scala aan fysieke netwerken, ze zouden uiteindelijk natuurkundig onderzoek kunnen ondersteunen dat zich richt op een breed scala aan onderwerpen.
"We gaan nu verder met de studie van fysieke netwerken, " zei Liu. "Momenteel, Ik werk aan één specifiek fysiek netwerk:het hersennetwerk van fruitvlieglarven, dat is een netwerk gevormd door neuronen ingebed in de 3D-ruimte. We zijn specifiek geïnteresseerd in de verbindingen tussen de lichamelijkheid van dit netwerk (zijn inbedding) en zijn structurele eigenschappen (hoe de neuronen zijn verbonden via neuronale bedradingen)."
© 2020 Wetenschap X Netwerk
 Hoe pathogene bacteriën een plakkerig adhesie-eiwit bereiden
Hoe pathogene bacteriën een plakkerig adhesie-eiwit bereiden Feiten over Nylon
Feiten over Nylon Hoe de hoeveelheid condensaat per hoeveelheid stoom te berekenen
Hoe de hoeveelheid condensaat per hoeveelheid stoom te berekenen Wetenschappers ontdekken dat hydratatie de sleutel is tot het verbeteren van de prestaties van katalysatoren voor industrieel gebruik
Wetenschappers ontdekken dat hydratatie de sleutel is tot het verbeteren van de prestaties van katalysatoren voor industrieel gebruik Buigbaar beton en andere met koolstof doordrenkte cementmengsels kunnen de wereldwijde uitstoot drastisch verminderen
Buigbaar beton en andere met koolstof doordrenkte cementmengsels kunnen de wereldwijde uitstoot drastisch verminderen
Hoofdlijnen
- Human Heart Science Projects
- Wat is Ceramide?
- Wat is Feedback-inhibitie en waarom is het belangrijk bij het reguleren van enzymactiviteit?
- Oceaanmonumenten worden geconfronteerd met mogelijk verlies van bescherming
- Stop en ga in het kaliumkanaal
- Hoe verschillende mierensoorten in hetzelfde territorium naast elkaar bestaan
- Genomische studie onderzoekt de evolutie van zachte killer-bijen in Puerto Rico
- Wat is lachtherapie?
- Wat is het doel van de fibreuze capsule?
- Hoe kosten per pond pond om te rekenen naar kosten per kilo /kg kg

- COSMIC-impact:next-gen röntgenmicroscopieplatform nu operationeel

- Arapuca-apparaat voor internationaal neutrino-experiment is verbeterd

- Avengers:Endgame maakt gebruik van tijdreizen en kwantummechanica terwijl het probeert het universum te herstellen

- Electron-photon smalltalk kan grote impact hebben op kwantumcomputers

 Nieuwe aanpak om gifstoffen uit afvalwater te verwijderen
Nieuwe aanpak om gifstoffen uit afvalwater te verwijderen Noord-Amerikaanse P-51 Mustang
Noord-Amerikaanse P-51 Mustang  Fotoherkenning die persoonlijke interesses privé houdt
Fotoherkenning die persoonlijke interesses privé houdt Doomsday prepping in tijden van coronavirus
Doomsday prepping in tijden van coronavirus Meer verzamelen dan alleen seismische gegevens langs de Cascadia Fault
Meer verzamelen dan alleen seismische gegevens langs de Cascadia Fault Aziatische vervuiling, hittegolven verergeren de Amerikaanse smog, studie toont
Aziatische vervuiling, hittegolven verergeren de Amerikaanse smog, studie toont Yellowstone verliest zijn sneeuw naarmate het klimaat warmer wordt, wijdverbreide problemen voorspellen voor water en dieren in het wild
Yellowstone verliest zijn sneeuw naarmate het klimaat warmer wordt, wijdverbreide problemen voorspellen voor water en dieren in het wild VN-vergadering begint met het opstellen van een plan voor een planeet zonder vervuiling
VN-vergadering begint met het opstellen van een plan voor een planeet zonder vervuiling
- Elektronica
- Biologie
- Zonsverduistering
- Wiskunde
- French | Italian | Spanish | Portuguese | Swedish | German | Dutch | Danish | Norway |

-
Wetenschap © https://nl.scienceaq.com

