
Wetenschap
4-D elektrisch circuitnetwerk met topologie
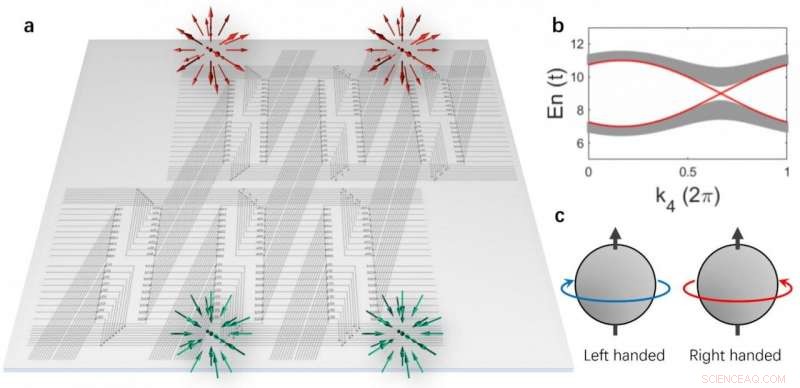
(a) Het 4D-circuitrooster gerealiseerd op een 2D-vlak. Een paar Weyl-punten met dezelfde chiraliteit zijn gelokaliseerd op de driedimensionale grens. (b) De bulkbandstructuren en de grens-Weyl-staten (rode lijnen). (c) Schema van de chiraliteit van Weyl-toestanden. Krediet:Science China Press
In recente jaren, topologie is naar voren gekomen als een belangrijk hulpmiddel om eigenschappen van materialen te classificeren en te karakteriseren. Het is gebleken dat veel materialen een aantal ongebruikelijke topologische eigenschappen vertonen, die niet worden aangetast door vervormingen, bijv. uitrekken, comprimeren, of draaien. Deze topologische eigenschappen omvatten gekwantiseerde Hall-stromen, grote magnetoweerstand, en oppervlakte-excitaties die immuun zijn voor wanorde. Het is te hopen dat deze eigenschappen kunnen worden gebruikt voor toekomstige technologieën, zoals, elektronica met laag vermogen, ultrasnelle detectoren, hoogrenderende energieomzetters, of voor kwantumcomputers.
Recenter, topologie is ook toegepast op synthetische materialen, bijv. fotonische kristallen of netwerken van elektrische circuits. Deze synthetische materialen hebben verschillende voordelen in vergelijking met hun natuurlijke tegenhangers. Bijvoorbeeld, de topologie van hun excitaties (d.w.z. hun excitatiebanden) kunnen nauwkeurig worden gecontroleerd en gemanipuleerd. In aanvulling, vanwege hun lange afstand rooster connectiviteit, synthetische materialen kunnen topologische excitaties realiseren in dimensies groter dan drie. Vandaar, Synthetische materialen, en in het bijzonder elektrische circuitnetwerken, bieden de mogelijkheid om een aantal interessante topologische eigenschappen te realiseren die niet toegankelijk zijn in echte materialen.
Rui Yu van de universiteit van Wuhan, Yuxin Zhao van de Universiteit van Nanjing, en Andreas Schnyder van het Max-Planck-Instituut Stuttgart hebben dit potentieel nu aangetoond door expliciet een elektrisch circuitnetwerk te construeren dat een vierdimensionale (4D) topologische isolator simuleert met een klassieke tijdomkeersymmetrie [Fig. 1(a)]. Topologische isolatoren zijn materialen die isolerend zijn in het bulkvolume, maar sterk geleidend aan de oppervlakte, als gevolg van gapless oppervlakte-excitaties. evenzo, de gesimuleerde 4-D topologische isolator heeft een excitatiegat in het bulkvolume, waarbinnen er een paar oppervlakte-excitaties bestaat [Fig. 1(b)].
Deze 3D oppervlakte-excitaties hebben een lineaire dispersie, en interessanter, ze zijn van het Weyl-type met dezelfde handigheid, d.w.z., ze hebben interne vrijheidsgraden die ronddraaien volgens dezelfde links- of rechtshandige regel met betrekking tot hun voortplantingsrichting [Fig. 1(c)]. Ze zijn van topologische oorsprong en zijn anders dan alle oppervlakte-excitatie die in conventionele materialen wordt aangetroffen. Topologie dicteert dat deze 3-D Weyl-excitaties in paren moeten komen en dat ze bestand zijn tegen wanorde en vervormingen. De auteurs hebben gedetailleerde numerieke simulaties van het topologische circuitnetwerk uitgevoerd en hebben aangetoond dat de 3-D Weyl-excitaties gemakkelijk kunnen worden waargenomen in frequentieafhankelijke metingen.
Het werk van de auteurs toont aan dat topologische excitaties gemakkelijk kunnen worden gerealiseerd op commercieel verkrijgbare printplaten of wafers met geïntegreerde schakelingen die zijn samengesteld uit inductoren en condensatoren. Het maakt de weg vrij voor het realiseren van willekeurige soorten topologische oppervlakte-excitaties, bijvoorbeeld, zogenaamde Dirac- of Majorana-excitaties van dimensie twee, drie, of zelfs hoger. De elektrische circuitimplementatie van topologische excitaties heeft het voordeel dat het eenvoudig is, gemakkelijk herconfigureerbaar, en een hoge mate van controle mogelijk maken. Dit zal het mogelijk maken om in de toekomstige topologische faseovergangen te bestuderen, niet-lineaire effecten, uit evenwicht verschijnselen, en quantum open systemen (bijv. niet-Hermitische systemen).
 Bestudeer polyfarmacologie eerder in medicijnontdekking, zeggen onderzoekers
Bestudeer polyfarmacologie eerder in medicijnontdekking, zeggen onderzoekers Een droom voor strandliefhebbers:een stap in de richting van langdurige zonnebrandcrème
Een droom voor strandliefhebbers:een stap in de richting van langdurige zonnebrandcrème Dubbel genot:nieuw synthetisch transmembraan-ionkanaal kan op twee manieren worden geactiveerd
Dubbel genot:nieuw synthetisch transmembraan-ionkanaal kan op twee manieren worden geactiveerd Superflexibele elektroluminescente apparaten ontwikkeld
Superflexibele elektroluminescente apparaten ontwikkeld Ontwerpen van selectieve reacties om biologische processen te moduleren
Ontwerpen van selectieve reacties om biologische processen te moduleren
 Wetenschappers hebben een oude meerbodem ontdekt diep onder het Groenlandse ijs
Wetenschappers hebben een oude meerbodem ontdekt diep onder het Groenlandse ijs Het microbioom van een oceaanbacterie verkennen
Het microbioom van een oceaanbacterie verkennen Voortbouwend op onze kennis van de aardbodem
Voortbouwend op onze kennis van de aardbodem Hoe jarenlang vechten tegen elke bosbrand de westerse megabranden van vandaag heeft aangewakkerd
Hoe jarenlang vechten tegen elke bosbrand de westerse megabranden van vandaag heeft aangewakkerd Toekomstige vulkaanuitbarstingen kunnen meer klimaatverstoring veroorzaken
Toekomstige vulkaanuitbarstingen kunnen meer klimaatverstoring veroorzaken
Hoofdlijnen
- Hoeveelheid water in stamcellen kan zijn lot bepalen als vet of bot
- Wetenschappers ontwikkelen microben om herinneringen aan hun omgeving te vormen
- Wanneer stopt het leven op aarde?
- Wat zijn de voor- en nadelen van flowcytometrie?
- Er is een genetische reden waarom Labrador Retrievers geobsedeerd zijn door voedsel
- Planten combineren kleur en geur om bestuivers te verkrijgen
- De verbazingwekkende diversiteit – en mogelijk verval – van paddenstoelen en andere schimmels
- DNA-replicatie vergelijken en contrasteren in prokaryoten en eukaryoten
- Een 3D-model van een plantencel bouwen
- Het gewicht van verplaatst water berekenen

- Dichtheid van koolzuurhoudend water

- Natuurkundigen brengen detector en versneller samen om nieuwe natuurkunde te verkennen die verder gaat dan het standaardmodel

- Onderzoekers verzenden gegevens via een halfgeleiderlaser, de deur openen naar ultrasnelle wifi
- Hoe worden exponenten gebruikt in het dagelijks leven?

 Scrollen door sprookjesfantasieën op sociale media kan je zelfvertrouwen vernietigen, maar het is niet allemaal slecht
Scrollen door sprookjesfantasieën op sociale media kan je zelfvertrouwen vernietigen, maar het is niet allemaal slecht Een studie legt de complexiteit uit van de vestiging van Azië door Homo sapiens
Een studie legt de complexiteit uit van de vestiging van Azië door Homo sapiens Onderzoekers laten zien dat korte laserpulsen selectief gouden nanodeeltjes verwarmen
Onderzoekers laten zien dat korte laserpulsen selectief gouden nanodeeltjes verwarmen Hayabusa2 laat doelmarkering vallen op asteroïde Ryugu
Hayabusa2 laat doelmarkering vallen op asteroïde Ryugu Wetenschappers verkleinen de vinbreedte van FinFET tot bijna de fysieke limiet
Wetenschappers verkleinen de vinbreedte van FinFET tot bijna de fysieke limiet Een ouderlijke paradox voor zwarte meisjes in het rechtssysteem
Een ouderlijke paradox voor zwarte meisjes in het rechtssysteem Het hebben van acne is positief geassocieerd met het algemene puntengemiddelde, voltooiing van de universiteit
Het hebben van acne is positief geassocieerd met het algemene puntengemiddelde, voltooiing van de universiteit Betere zonnecellen, beter LED-licht en enorme optische mogelijkheden
Betere zonnecellen, beter LED-licht en enorme optische mogelijkheden
- Elektronica
- Biologie
- Zonsverduistering
- Wiskunde
- French | Spanish | Portuguese | Swedish | German | Dutch | Danish | Norway | Italian |

-
Wetenschap © https://nl.scienceaq.com

