Wetenschap
Nieuw kunstmatig neuraal netwerkmodel overtreft MaxEnt in invers probleemvoorbeeld
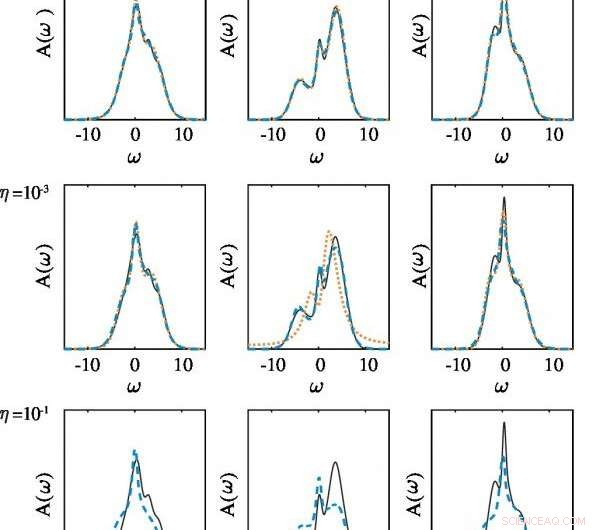
Vergelijking van de spectrale beginfuncties A(ω) (ononderbroken lijnen) met de voorspelde Aˆ(ω) berekend met de MaxEnt-benadering (oranje stippellijnen) en het voorgestelde ANN-model (blauwe stippellijnen) bij verschillende geluidsniveaus η voor drie voorbeelden van spectrale dichtheidsfuncties die niet aanwezig zijn in de trainingsdataset. ANN gedraagt zich even goed als MaxEnt bij een laag geluidsniveau, maar veel beter dan MaxEnt bij een hoog geluidsniveau. Krediet:EPFL
Numerieke simulaties, over het algemeen gebaseerd op vergelijkingen die een bepaald model beschrijven en op initiële gegevens, worden toegepast in een steeds groter wordend scala aan wetenschappelijke disciplines om processen op bepaalde punten in tijd en ruimte te benaderen. Bij zogenaamde inverse problemen, deze kritieke gegevens ontbreken - onderzoekers moeten benaderingen van de invoergegevens of van het model dat ten grondslag ligt aan waarneembare gegevens reconstrueren om de gewenste voorspellingen te genereren.
Hoewel er al technieken bestaan om dit te doen, ze zijn slecht gedefinieerd, niet in staat om unieke interpretaties of waarden toe te kennen aan een bepaald punt. Als voorbeeld, in de meest gebruikte methode om dergelijke problemen op te lossen, de zogenaamde maximale entropie (MaxEnt) benadering, voorkennis wordt toegevoegd door een standaardverdeling op te geven die overeenkomt met de verwachte resultaten bij afwezigheid van gegevens. Het algoritme zoekt iteratief naar een distributie die entropie maximaliseert met betrekking tot deze standaarddistributie, terwijl het ook een functie genereert die dicht bij bestaande gegevens ligt. De benadering omvat een parameter die wordt gebruikt om het relatieve belang tussen de entropie en de fouttermen af te wegen. Er zijn verschillende methoden om het te repareren die in de praktijk vaak verschillende resultaten opleveren.
In de paper Artificial Neural Network Approach to the Analytic Continuation Problem, Quan Sheng Wu, een wetenschapper en Romain Fournier, een masterstudent aan EPFL's C3MP, onder leiding van professor Oleg Yazyev, en collega professor Lei Wang van het instituut voor natuurkunde van de Chinese Academie van Wetenschappen presenteren een gesuperviseerde leerbenadering van het probleem. Gebaseerd op een artificieel neuraal netwerk (ANN) - zeer veelzijdig dankzij het vermogen om continue functies te benaderen onder milde aannames en vanwege krachtige bibliotheken die de efficiënte implementatie van verschillende ANN-architecturen mogelijk maken die kunnen worden aangepast om te profiteren van gegevensstructuren - de nieuwe methode lijkt net zo nauwkeurig als MaxEnt en aanzienlijk goedkoper rekenkundig.
In een eerste test van het ANN-raamwerk, de onderzoekers kozen ervoor om een systeem te onderzoeken dat een analytische oplossing heeft, maar is moeilijk op te lossen met MaxEnt, namelijk de tijdcorrelatiefunctie van de positie-operator voor een harmonische oscillator die lineair is gekoppeld aan een ideale omgeving. de Hamiltoniaan, of operator die in het algemeen overeenkomt met de totale energie van het systeem, is in dit geval bekend, en de gegevens van belang - de denkbeeldige tijdcorrelatiefunctie - kunnen worden gegenereerd door quantum Monte Carlo (QMC) -simulaties.
De analytische oplossing geeft de relatie tussen het vermogensspectrum en een denkbeeldige tijdcorrelatiefunctie en verschaft als zodanig fysiek relevante trainingsgegevens voor het ANN-model. De onderzoekers trainden de ANN met de gegenereerde gegevens en testten deze vervolgens door de denkbeeldige tijdcorrelatiefunctie te verkrijgen die in de eerdere stap door QMC was berekend. Het op de gehele dataset getrainde model toonde bijna perfecte overeenstemming met de analytische oplossing. MaxEnt gaf geen nauwkeurige resultaten, hoewel de onderzoekers opmerkten dat betere resultaten waarschijnlijk zouden zijn verkregen door de correlatiefunctie op een groter aantal punten te berekenen.
Om het model verder praktisch te testen, de onderzoekers probeerden de spectrale dichtheid van een enkelvoudig elektron in het reële frequentiedomein te herstellen van de functie van een Green in het denkbeeldige tijdsdomein. Hoewel zowel de ANN- als de MaxEnt-modellen in staat waren om de beginspectrale functies nauwkeurig te voorspellen voor het laagste ruisniveau, MaxEnt had de neiging om pieken in de voorspelde spectrale functie te onderdrukken met toenemende ruis in het systeem. Deze resultaten laten zien dat het ANN-model veelzijdig en robuust is tegen gegevens met veel ruis.
De nieuwe methode is ook rekenkundig efficiënter. ANN stond directe mapping toe tussen de functies van Green en de spectrale dichtheden en kan in die zin het probleem direct oplossen. MaxEnt daarentegen is iteratief en genereert proeffuncties totdat convergentie is bereikt. Met de rekenopstelling die in de paper wordt gebruikt, de tijd die nodig was voor het converteren van een bepaald aantal paren bij een bepaald ruisniveau was 5 seconden in het geval van ANN vergeleken met de 51 minuten die MaxEnt nodig zou hebben gehad met dezelfde opstelling.
De onderzoekers zeiden dat dergelijke ANN's waarschijnlijk andere inverse problemen kunnen oplossen, op voorwaarde dat relevante datasets - afgeleid, bijvoorbeeld, met behulp van beschikbare experimentele resultaten in combinatie met data-augmentatietechnieken kunnen worden geconstrueerd. De getrainde modellen die het resultaat zijn van het werk kunnen hier worden verkregen uit een openbare repository op GitHub:github.com/rmnfournier/ACANN.
 Nieuw polymeermengsel creëert ultragevoelige warmtesensor
Nieuw polymeermengsel creëert ultragevoelige warmtesensor Zeldzaam glasachtig metaal ontdekt tijdens zoektocht om batterijprestaties te verbeteren
Zeldzaam glasachtig metaal ontdekt tijdens zoektocht om batterijprestaties te verbeteren Wat gebeurt er als je azijn toevoegt aan schelpen?
Wat gebeurt er als je azijn toevoegt aan schelpen?  Onderzoekers brengen de bling om implantaten te verbeteren
Onderzoekers brengen de bling om implantaten te verbeteren Elektriciteit gebruiken om verontreinigende stoffen die overblijven na afvalwaterzuivering af te breken
Elektriciteit gebruiken om verontreinigende stoffen die overblijven na afvalwaterzuivering af te breken
 De verwarming hoger zetten op afgelegen onderzoekspercelen zonder elektriciteit
De verwarming hoger zetten op afgelegen onderzoekspercelen zonder elektriciteit Vulkaan Guatemala spuwt as maanden na dodelijke uitbarsting
Vulkaan Guatemala spuwt as maanden na dodelijke uitbarsting Dodental van Filippijnse storm, aardverschuivingen klimmen naar 126
Dodental van Filippijnse storm, aardverschuivingen klimmen naar 126 Het verschil tussen harde en zachte tarwe
Het verschil tussen harde en zachte tarwe  Bemanningen worstelen om het vuur op Lake Tahoe te stoppen
Bemanningen worstelen om het vuur op Lake Tahoe te stoppen
Hoofdlijnen
- Sumatraanse neushoorns zijn nooit hersteld van verliezen tijdens het Pleistoceen, genoom bewijs toont
- Nieuwe slangensoort verstopt zich in het volle zicht
- Nieuwe studie verandert kijk op vliegende insecten
- Wat zijn Agar Slants?
- Hoe je gistademhaling meet
- Mensen gebruiken niet zoveel denkkracht als we graag denken
- Moet je intelligent zijn om slecht te zijn?
- Tot 50% minder fytosanitaire producten nodig om wijnstokziekten te behandelen
- Wat is een molecuul dat wordt geproduceerd door DNA uit twee verschillende bronnen te combineren?
 Grafeen helpt fotokathoden te beschermen voor natuurkundige experimenten
Grafeen helpt fotokathoden te beschermen voor natuurkundige experimenten Hoe kan de maan ons schone energie geven?
Hoe kan de maan ons schone energie geven?  Smartphone-apps kunnen verbinding maken met kwetsbare backend-cloudservers
Smartphone-apps kunnen verbinding maken met kwetsbare backend-cloudservers Een model maken Stikstofatomen
Een model maken Stikstofatomen Wetenschappers doen magnetische nieuwe ontdekking van grafeen
Wetenschappers doen magnetische nieuwe ontdekking van grafeen US West bereidt zich voor op mogelijke eerste verklaring van watertekort
US West bereidt zich voor op mogelijke eerste verklaring van watertekort Nanodeeltjes graven 's werelds kleinste tunnels
Nanodeeltjes graven 's werelds kleinste tunnels NASA vangt tropische storm Francisco's nadering van aanlanding in het zuiden van Japan
NASA vangt tropische storm Francisco's nadering van aanlanding in het zuiden van Japan
- Elektronica
- Biologie
- Zonsverduistering
- Wiskunde
- French | Italian | Portuguese | Swedish | German | Dutch | Danish | Norway | Spanish |

-
Wetenschap © https://nl.scienceaq.com