
Wetenschap
Hoe klein is een small-world netwerk?
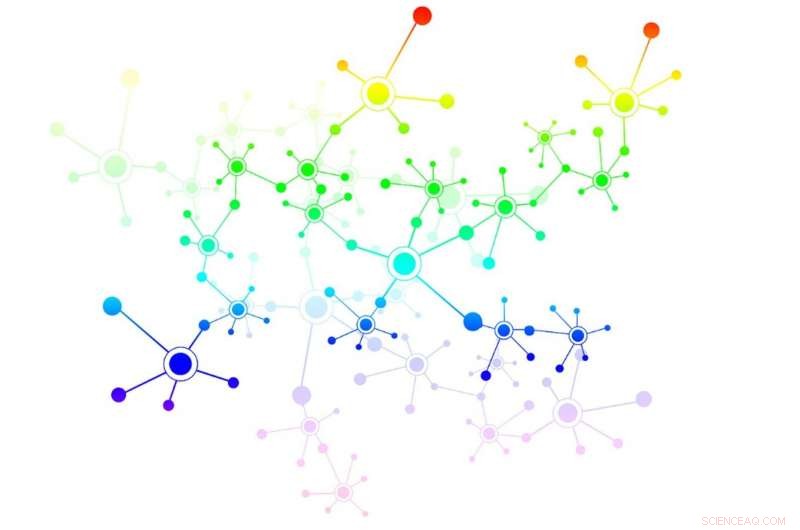
De small-world eigenschap is een eigenschap van netwerken waarin, ondanks een groot aantal knooppunten, het is mogelijk om korte communicatiepaden tussen hen te vinden. Krediet:UPF
Ontdekt in de sociale wetenschappen in de jaren 60, het fenomeen dat bekend staat als netwerken van de kleine wereld, fascineert de populaire cultuur en wetenschap al tientallen jaren. Het kwam voort uit de observatie dat in de wereld, twee willekeurige mensen zijn verbonden door een korte keten van sociale banden.
Een netwerk, of het nu natuurlijk (neuraal of sociaal) of kunstmatig (communicatie- of transportsystemen) is, het is een geordende reeks elementen die met elkaar zijn verbonden via verschillende methoden die informatie delen. De small-world eigenschap is een eigenschap van netwerken waarin, ondanks een groot aantal knooppunten, het is mogelijk om korte communicatiepaden tussen hen te vinden. In de afgelopen decennia is bewezen dat zowel in natuurlijke als in kunstmatige systemen, veel echte netwerken zijn ook klein. Maar, zijn alle kleine wereldnetwerken klein, en hoe verhouden ze zich tot anderen?
In de fysieke wereld evalueren en vergelijken we de grootte van objecten door ze te vergelijken met een gemeenschappelijke referentie, meestal een standaard metrisch systeem gedefinieerd en goedgekeurd door de gemeenschap. Bij complexe netwerken het verschil is dat elk netwerk zijn eigen metrische ruimte vormt. Dus, de vraag of een netwerk kleiner of groter is dan een ander impliceert de vergelijking van twee verschillende ruimtes met elkaar, in plaats van de meer bekende situatie waarin twee objecten worden gecontrasteerd binnen de ruimte die ze delen.
Ondanks de bestaande verscheidenheid aan kleine wereldnetwerken, het blijft nog steeds een uitdaging om een betrouwbare en vergelijkbare meting van hun gemiddelde lengte te maken.
Het belangrijkste resultaat van een studie gepubliceerd in Natuur Communicatie Natuurkunde op 14 november is "de identificatie van de onder- en bovengrenzen voor de gemiddelde padlengte en globale efficiëntie voor (di) grafieken van willekeurig aantal knooppunten en links, " beweren Gorka Zamora-Lopez, een onderzoeker bij het Center for Brain and Cognition (CBC) bij de afdeling Informatie- en Communicatietechnologie (DTIC) en Romain Brasselet, een onderzoeker aan de International School for Advanced Studies (SISSA) in Triëst (Italië), auteurs van het werk.
"We kunnen nu de gemiddelde padlengte van een netwerk beoordelen - van een bepaalde grootte en dichtheid - door te evalueren hoeveel het afwijkt van de kleinste en de grootste padlengte die het mogelijk zou kunnen nemen, " Zamora López en Brasselet commentaar.
Deze resultaten maken het mogelijk om de lengte van een netwerk te karakteriseren onder een natuurlijke referentie en bieden een synoptische weergave, zonder de noodzaak om te kiezen tussen willekeurig gegenereerde modellen (willekeurige grafieken) zoals tot nu toe het geval was. Met andere woorden, "Dit theoretische kader stelt ons in staat om zowel empirische netwerken als grafiekmodellen samen te evalueren onder hetzelfde referentiekader. Hoewel de padlengte van deze constructies vergelijkbaar is, hun dynamische eigenschappen kunnen aanzienlijk verschillen, " voegen ze eraan toe.
De implicaties van deze resultaten overstijgen de puur structurele studie van netwerken. Door dit theoretisch kader toe te passen op empirische voorbeelden van drie categorieën (neuraal, sociaal en transport) laat zien dat, terwijl de meeste echte netwerken een padlengte vertonen die vergelijkbaar is met die van willekeurige grafieken, in tegenstelling tot de boven- en ondergrenzen, alleen de neurale netwerken, d.w.z., de corticale connectomen, blijken ultrakort te zijn.
De auteurs concluderen dat problemen met netwerkoptimalisatie de maximalisatie van een verscheidenheid aan parameters met zich meebrengen. De resultaten die ze hebben verkregen, zijn de oplossingen voor het eenvoudigste geval met een minimale reeks beperkingen. Deze oplossingen kunnen dienen als startpunt voor het bestuderen van complexere problemen die extra beperkingen bevatten die verder gaan dan het aantal knooppunten en koppelingen.
 Onderzoekers laten zien dat materialen vanzelf sterker worden wanneer ze met zeer hoge snelheid worden geraakt
Onderzoekers laten zien dat materialen vanzelf sterker worden wanneer ze met zeer hoge snelheid worden geraakt Nieuwe immunotherapietechniek kan specifiek gericht zijn op tumorcellen, studieverslagen
Nieuwe immunotherapietechniek kan specifiek gericht zijn op tumorcellen, studieverslagen Wat betekent neutralisatie?
Wat betekent neutralisatie?  5de rang Chemieversleuteld activiteit
5de rang Chemieversleuteld activiteit Hoe equivalente eenheden te berekenen
Hoe equivalente eenheden te berekenen
Hoofdlijnen
- Galapagos-studie toont aan dat nieuwe soorten zich in slechts twee generaties kunnen ontwikkelen
- Nieuw algoritme herkent duidelijke dolfijnklikken in onderwateropnamen
- Niet zo koude eend? Man blijft zoeken naar uitgestorven vogel
- De structuur die het cytoplasma in een bacteriecel omringt
- Bootverkeer bedreigt het voortbestaan van de Bocas Del Toro-dolfijnen in Panama
- Hoe Dopamine sommige voedingsmiddelen verslavend maakt
- Hoe maak je een 3D-model van het spierstelsel voor een wetenschapsklasse
- Waarom het zo moeilijk is om schepen bij te houden die niets goeds doen?
- Organisme: definitie, types, kenmerken en voorbeelden
- Onderzoekers stellen een verklaring voor voor het mysterieuze begin van een universeel proces

- Dynamische aspirine - moleculaire trillingen drijven elektronen over grote afstanden aan
- Nieuwe modelleringsmethode vestigt de aandacht op amorfe materialen ongebruikelijke trillingsmodi
- Onderzoekers weerleggen leerboekkennis over moleculaire interacties
- De kristallijne orde verstoren om de superfluïditeit te herstellen

 Detectie van verontreinigingen met één molecuul, explosieven of ziekten nu mogelijk
Detectie van verontreinigingen met één molecuul, explosieven of ziekten nu mogelijk Nieuw AI-systeem beheert wegeninfrastructuur via Google Street View
Nieuw AI-systeem beheert wegeninfrastructuur via Google Street View Wetenschapper ontwikkelde 3D-scans van kevers voor Blade Runner 2049
Wetenschapper ontwikkelde 3D-scans van kevers voor Blade Runner 2049 Nieuw proces verandert papierproductieafval in waardevolle chemicaliën
Nieuw proces verandert papierproductieafval in waardevolle chemicaliën Is zweten endotherm of exotherm?
Is zweten endotherm of exotherm?  FBI sluit zich aan bij onderzoek naar olieramp in Orange County
FBI sluit zich aan bij onderzoek naar olieramp in Orange County Journalisten onderzoeken Rusland doelwit van cyberaanvallen:ProtonMail
Journalisten onderzoeken Rusland doelwit van cyberaanvallen:ProtonMail Xerox beëindigt fusie met Fujifilm in overwinning voor aandeelhouders
Xerox beëindigt fusie met Fujifilm in overwinning voor aandeelhouders
- Elektronica
- Biologie
- Zonsverduistering
- Wiskunde
- French | Italian | Spanish | Portuguese | Swedish | German | Dutch | Danish | Norway |

-
Wetenschap © https://nl.scienceaq.com

