
Wetenschap
Kwantumruimtetijd op een kwantumsimulator
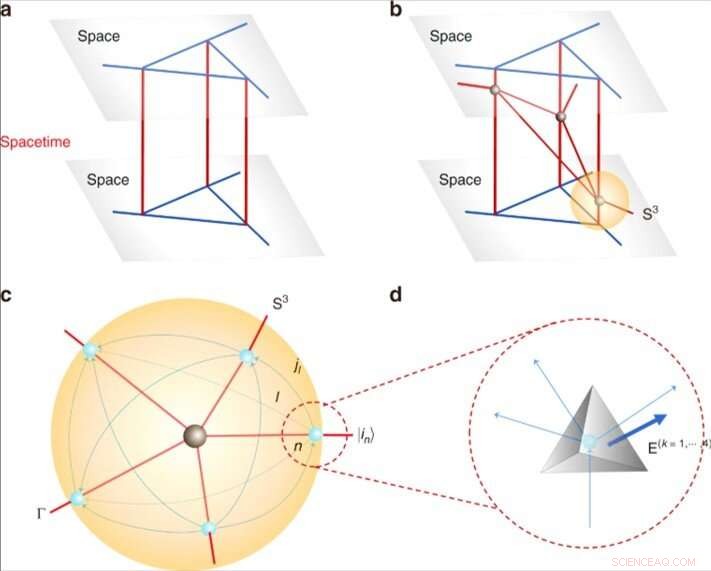
Kwantumruimtetijd en tetraëders. (a) Een statische 4d kwantumruimtetijd van de evolutie van het spinnetwerk. (b) Een dynamische kwantumruimtetijd met een aantal van vijf valente hoekpunten (in zwart) door elkaar snijdende wereldbladen, waarvan er één wordt aangeduid met S3. (c) De lokale structuur van een hoekpunt van b door een 3-bol S3 te beschouwen die het hoekpunt omsluit. Snijpunten tussen de wereldbladen en S3 geven een spinnetwerk (in blauw). Elk spinnetwerk vertegenwoordigt een toestand |in⟩ en elke link l is georiënteerd, die een half geheel getal jl draagt. (d) Quantum geometrische tetraëders. Elk knooppunt van het spinnetwerk vertegenwoordigt een kwantumtetraëder. Het verbinden van 2 knooppunten door een schakel in het spinnetwerk komt overeen met het lijmen van 2 tetraëders door het vlak dubbel aan de schakel. Georiënteerde gebieden worden aangeduid met E(k=1, ik, 4)=(E(k)x, E(k)j, E(k)z). Krediet:communicatiefysica, doi:10.1038/s42005-019-0218-5
Kwantumsimulatie speelt een onvervangbare rol op diverse terreinen, buiten het bereik van klassieke computers. In een recente studie, Keren Li en een interdisciplinair onderzoeksteam van het Center for Quantum Computing, Quantum Science and Engineering en het Department of Physics and Astronomy in China, VS Duitsland en Canada. Experimenteel gesimuleerde spin-netwerktoestanden door kwantumruimtetijd-tetraëders te simuleren op een vier-qubit nucleaire magnetische resonantie (NMR) kwantumsimulator. De experimentele getrouwheid was boven de 95 procent. Het onderzoeksteam gebruikte de kwantumtetraëders bereid door nucleaire magnetische resonantie om een tweedimensionale (2-D) spinfoam vertex (model) amplitude te simuleren, en lokale dynamiek van kwantumruimtetijd weer te geven. Li et al. de geometrische eigenschappen van de overeenkomstige kwantumtetraëders gemeten om hun interacties te simuleren. Het experimentele werk is een eerste poging en een basismodule om het Feynman-diagramhoekpunt in de spinfoam-formulering weer te geven, om lus kwantumzwaartekracht (LQG) te bestuderen met behulp van kwantuminformatieverwerking. De resultaten zijn nu beschikbaar op Communication Physics.
Klassieke computers kunnen grote kwantumsystemen niet bestuderen ondanks succesvolle simulaties van een verscheidenheid aan fysieke systemen. De systematische beperkingen van klassieke computers deden zich voor toen de lineaire groei van de grootte van het kwantumsysteem overeenkwam met de exponentiële groei van de Hilbert-ruimte, een wiskundige basis van de kwantummechanica. Kwantumfysici proberen dit probleem op te lossen door kwantumcomputers te gebruiken die informatie intrinsiek of kwantummechanisch verwerken om exponentieel beter te presteren dan hun klassieke tegenhangers. 1982, Natuurkundige Richard Feynman definieerde kwantumcomputers als kwantumsystemen die kunnen worden bestuurd om het gedrag of de eigenschappen van relatief minder toegankelijke kwantumsystemen na te bootsen of te simuleren.
In het huidige werk, Li et al. gebruikte nucleaire magnetische resonantie (NMR) met een hoge regelbare prestatie op het kwantumsysteem om simulatiemethoden te ontwikkelen. De strategie vergemakkelijkte de presentatie van kwantumgeometrieën van ruimte en ruimtetijd op basis van de analogieën tussen kernspintoestanden in NMR-monsters en spinnetwerktoestanden in kwantumzwaartekracht. Kwantumzwaartekracht heeft tot doel de Einstein-zwaartekracht te verenigen met de kwantummechanica om ons begrip van zwaartekracht uit te breiden naar de Planck-schaal (1,22 x 10 19 GeV). Op de Planck-schaal (grootheden van de ruimte, tijd en energie) Einstein-zwaartekracht en het continuüm van ruimtetijdafbraak kunnen worden vervangen via kwantumruimtetijd. Onderzoeksbenaderingen voor het begrijpen van kwantumruimtetijden zijn momenteel geworteld in spinnetwerken (een grafiek van lijnen en knooppunten om de kwantumtoestand van de ruimte op een bepaald moment in de tijd weer te geven), die een belangrijk, niet-perturbatief raamwerk van kwantumzwaartekracht.
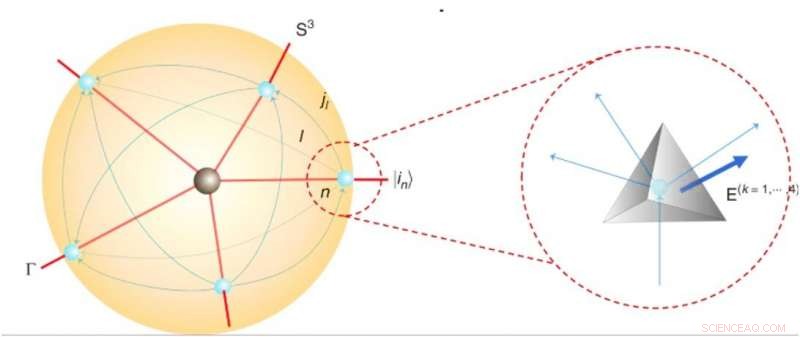
Kwantumruimtetijd en tetraëders binnen een spinnetwerk. Krediet:communicatiefysica, doi:10.1038/s42005-019-0218-5
1971, natuurkundige Roger Penrose stelde spin-netwerken voor die werden gemotiveerd door de twistor-theorie met daaropvolgende toepassingen om kwantumzwaartekracht (LQG) te lussen. De spinnetwerken waren kwantumtoestanden die fundamenteel discrete kwantumgeometrieën van de ruimte op de Planck-schaal vertegenwoordigen. In de huidige studie, het onderzoeksteam stelde het spinnetwerk voor met behulp van een grafiek met links en knooppunten gekleurd door spinhelften. Bijvoorbeeld, elk knooppunt met randen kwam overeen met een geometrie en daarom kwam een grafiek met vierwaardige knooppunten overeen met de kwantumtetraëdergeometrie.
Het onderzoeksteam ontwikkelde een "netwerk" met daarin een aantal driedimensionale (3-D) wereldbladen (2-D-oppervlakken) en hun snijpunten. Ze toonden aan dat elk hoekpunt waar de oppervlakken elkaar ontmoetten, leidde tot een kwantumtransitie die het spinnetwerk veranderde om de lokale dynamiek van de kwantumgeometrie weer te geven. Net zoals Feynman-diagrammen (schematische weergaven van wiskundige uitdrukkingen die het gedrag van subatomaire deeltjes beschrijven), kwantumruimtetijden codeerden de overgangsamplitudes en spinfoamamplitudes tussen de initiële en laatste spinnetwerken. De kwantumruimtetijden en spinfoamamplitudes die in het onderzoek zijn ontwikkeld, zorgden voor een consistente en veelbelovende benadering van kwantumzwaartekracht. Li et al. kenmerkte de NMR-simulatie door de mogelijkheid om individuele qubits met hoge precisie te besturen. De kwantumtetraëders en vertexamplitudes dienden als bouwstenen van LQG (loop quantum gravity) om een nieuw venster te openen om LQG op te nemen in kwantumexperimenten.
De wetenschappers hebben eerst vergelijkingen afgeleid om een kwantumtetraëder binnen een spinnetwerk te beschrijven. In een schematisch 3+1-dimensionaal dynamisch kwantumruimtetijdmodel, ze demonstreerden een atoom als een 3-bol die een deel van de kwantumruimtetijd omsluit rond een hoekpunt. Het team modelleerde de grens van de omsloten kwantumruimtetijd precies als een spinnetwerk en toonde de mogelijkheid aan om grote kwantumruimtetijden met veel hoekpunten te simuleren door de atomen kwantum te lijmen. De resulterende structuur leek op de vertexamplitude van kwantumruimtetijd, vergelijkbaar met eerder ontwikkelde Ooguri's topologische roostermodellen in vier dimensies. De onderzoekers lieten LQG zien om kwantumtetraëdergeometrieën te identificeren met de kwantumhoekmomenta. Door de identificatie konden ze kwantumgeometrieën simuleren met kwantumregisters (kwantummechanische analoog van een klassiek processorregister). In het algemeen, een kwantumregister kan wiskundig worden bereikt met behulp van tensorproducten.
BOVEN:Experimenteel voorbereide toestanden op de Bloch-bol en hun overeenkomstige klassieke tetraëders. De toestanden hebben de vorm cosθ2|0⟩L+eiϕsinθ2|1⟩L en worden gelabeld door Ai, Bi, ci, Di, Ei (i=0, 1), waaronder, C0 en C1 zijn regelmatige tetraëders. |0L⟩ en |1L⟩ zijn de basistoestanden in een deelruimte van een vier-qubitsysteem, die een enkele logische qubit vertegenwoordigt. ONDER:Cosinuswaarden van hoeken tussen vlaknormalen in de kwantumtetraëder (cosinus van tweevlakshoeken verschillen met een minteken). De resultaten in experimenten (theorie) worden weergegeven door de gekleurde (transparante) kolommen. Foutbalken kwamen van de onzekerheid bij het passen van nucleaire magnetische resonantie (NMR) spectra. Krediet:communicatiefysica, doi:10.1038/s42005-019-0218-5 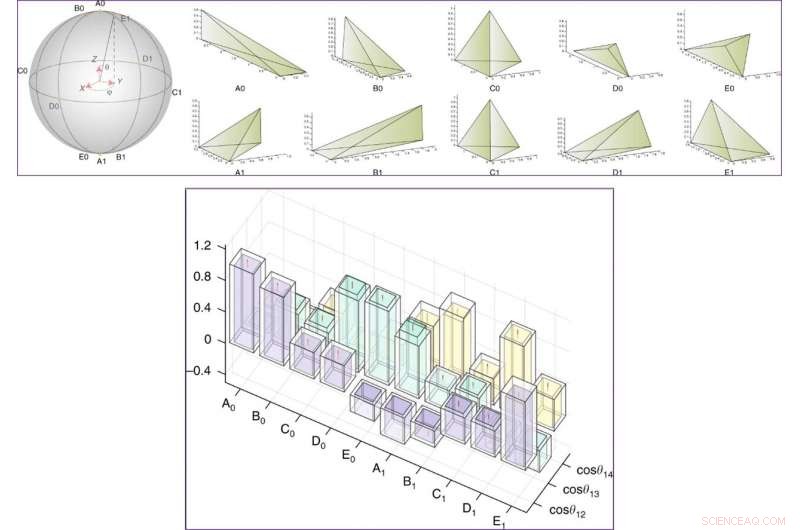
- Voor staatsvoorbereiding, eerst initialiseerden ze het hele systeem naar een pseudo-zuivere staat. Ze behaalden een getrouwheid van meer dan 99 procent met behulp van de ruimtelijk gemiddelde methode. Daarna dreven ze het systeem in 10 invariante-tensortoestanden of transformaties, die ze implementeerden met behulp van 10 gevormde pulsen van 20 ms.
- Volgende, voor geometriemetingen, het team presenteerde de gemeten geometrie-eigenschappen met behulp van een 3D-histogram. De experimentele onzekerheid op dit punt was het gevolg van het NMR-spectrumaanpassingsproces. Het samenvallen tussen experimentele en theoretische simulaties impliceerde dat de invariante tensortoestanden die in de experimenten waren voorbereid, overeenkwamen met de bouwstenen - kwantumtetraëders.
- Tijdens amplitudesimulatie, de spin-netwerktoestanden dienden als de grensgegevens van 3+1-dimensionale kwantumruimtetijd. De vertex-amplitude gedefinieerd in de studie bepaalde de spinfoam-amplitude en beschreef de lokale dynamiek van kwantumzwaartekracht in 4-D kwantumruimtetijd, om de eigenschappen van deze grensgegevens weer te geven.
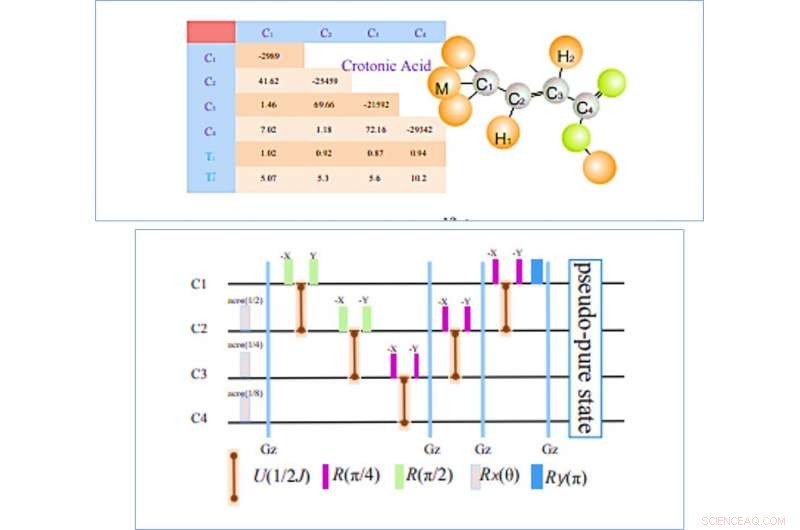
LINKS:Structuur van crotonzuurmolecuul; De vier 13C-kernen worden aangeduid als de vier qubits en de tabel aan de linkerkant geeft de parameters weer die de interne Hamiltoniaan construeren. Chemische verschuivingen (Hz), J-koppelingssterkten (Hz) en de relaxatietijden (T1 en T2) staan vermeld in het diagonale gedeelte, niet-diagonale elementen en de bodem, respectievelijk. Alle parameters werden gemeten op een Bruker DRX 700 MHz spectrometer bij kamertemperatuur. RECHTS:Pulssequenties voor het creëren van de pseudo-zuivere staat. Op basis van de ruimtelijke gemiddelde techniek, de circuits omvatten lokale operaties, vijf J-koppeling evoluties, en vier z-gradiëntpulsen om de ongewenste coherente termen te vernietigen. de duur van 1/2J vrije evolutie hangt af van de sterkte van de J-koppeling tussen relevante spins. Krediet:communicatiefysica, doi:10.1038/s42005-019-0218-5
Om de hoekpuntamplitudes te verkrijgen, de onderzoekers berekenden de inproducten tussen vijf verschillende kwantumtetraëdertoestanden. Ideaal, de onderzoekers hadden een kwantumcomputer van 20 qubit kunnen gebruiken, het vaststellen van maximaal verstrengelde toestanden van twee qubits tussen twee willekeurige tetraëders. Echter, aangezien een kwantumcomputer van dergelijke afmetingen momenteel verder gaat dan de gecommercialiseerde geavanceerde technologie, de onderzoekers voerden afwisselend volledige tomografie uit van de staatsvoorbereiding om informatie te verkrijgen over kwantumtetraëdertoestanden. Toen de wetenschappers de getrouwheid berekenden tussen de experimentele kwantumtetraëdertoestanden en de theorie, de resultaten waren ruim boven de 95 procent. Met behulp van de kwantumtetraëders, het onderzoeksteam simuleerde de vertex-amplitude. Ze vergeleken de resultaten tussen het experiment en de numerieke simulatie tussen alle vijf tetraëders. Overeenkomstig, zadelpunten van de amplitude in de experimenten deden zich voor waar de vijf interagerende tetraëders een eenvoudige geometrische betekenis vertoonden terwijl ze aan elkaar plakten om een geometrische vier-simplex te vormen.
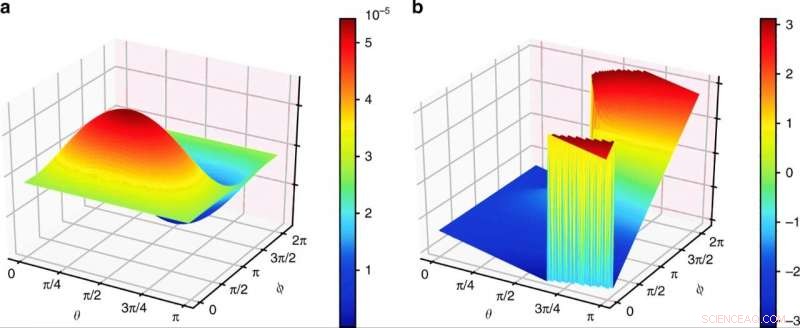
Resultaten van gesimuleerde hoekpuntamplitudes a zijn de amplitude van Vgl. (3) en b beschrijven de informatie van zijn fase. θ en ϕ zijn de parameters van de vier-qubit invariant-tensortoestand die overeenkomt met de bolcoördinaten op de Bloch-bol. Krediet:communicatiefysica, doi:10.1038/s42005-019-0218-5
Op deze manier, Keren Li en collega's gebruikten een kwantumregister in het NMR-systeem om 10 invariante-tensortoestanden te creëren om 10 kwantumtetraëders weer te geven. Ze bereikten een getrouwheid van meer dan 95 procent en maten vervolgens de tweevlakshoeken (twee vlakke vlakken) van het model. Ze overwogen de fouten in het spectrum en de geometrische identificatie om het succes te begrijpen bij het simuleren van kwantumtetraëders in het onderzoek. Het nieuwe onderzoekswerk presenteerde een eerste stap om spin-netwerktoestanden en spinschuimamplitudes te verkennen met behulp van een kwantumsimulator. Het begeleidende werk toonde ook geldige experimenten om LGQ te bestuderen.
© 2019 Wetenschap X Netwerk
 Onderzoek onthult meer over het pad dat bacteriële ziekteverwekkers afleggen om tuberculose te veroorzaken
Onderzoek onthult meer over het pad dat bacteriële ziekteverwekkers afleggen om tuberculose te veroorzaken Nieuwe methode helpt orthotope beeldvorming van hersentumoren duidelijker en sneller te maken
Nieuwe methode helpt orthotope beeldvorming van hersentumoren duidelijker en sneller te maken Hoe een sterisch getal berekenen
Hoe een sterisch getal berekenen  Nieuw maskermateriaal kan nanodeeltjes van virusgrootte verwijderen
Nieuw maskermateriaal kan nanodeeltjes van virusgrootte verwijderen Wetenschappers ontdekken natuurlijke plantaardige conserveermiddelen
Wetenschappers ontdekken natuurlijke plantaardige conserveermiddelen
 NASA-satelliet vindt Jongdari een tropische depressie
NASA-satelliet vindt Jongdari een tropische depressie Het vernietigen van de rivierbossen van Nigeria is slecht voor het zoetwaterecosysteem
Het vernietigen van de rivierbossen van Nigeria is slecht voor het zoetwaterecosysteem Als de opwarming van de aarde stopt, zeeën zullen nog steeds stijgen:studie
Als de opwarming van de aarde stopt, zeeën zullen nog steeds stijgen:studie Onderzoekers ontwerpen voorspellingssysteem voor droogte tijdens een seizoen
Onderzoekers ontwerpen voorspellingssysteem voor droogte tijdens een seizoen Uit onderzoek blijkt dat aardbevingen nog jaren doorgaan nadat de injectie van afvalwater in het gasveld is gestopt
Uit onderzoek blijkt dat aardbevingen nog jaren doorgaan nadat de injectie van afvalwater in het gasveld is gestopt
Hoofdlijnen
- Wetenschappers ontcijferen mechanismen die ten grondslag liggen aan de biologie van veroudering
- Wat zijn de voor- en nadelen van flowcytometrie?
- Veel meer bacteriën hebben elektrisch geleidende filamenten
- Het belang van DNA in de menselijke cel
- Team onthult hoge prevalentie van bacteriën die gen mcr-1 dragen in ecosysteem
- Doen eukaryote cellen door binaire fissie?
- Industrieel gebruik van Pepsin
- Hoe een biologisch diagram te tekenen
- EU-lidstaten stemmen volgende maand over vijfjarige verlenging van onkruidverdelger
- Innovatieve methode biedt een nieuwe manier om de ontwikkelingsbiomechanica van het hart te bestuderen, woon in 4-D
- ATLAS Experiment geeft 13 TeV LHC open data vrij voor wetenschappelijk onderwijs

- Optische trekstraal houdt bacteriën vast
- Twisted physics:Magische hoek grafeen produceert schakelbare patronen van supergeleiding

- Nucleair terrorisme kan worden onderschept door neutronen-gamma-detector die de bron lokaliseert

 Onderzoekers ontdekken een stukje Amerika in het noorden van Australië
Onderzoekers ontdekken een stukje Amerika in het noorden van Australië De landschapsmarkt heeft een categorie voor elk activiteitenniveau
De landschapsmarkt heeft een categorie voor elk activiteitenniveau Libanon laat oude tanks zinken om onderwaterduikpark te creëren
Libanon laat oude tanks zinken om onderwaterduikpark te creëren Iran lanceert komende dagen twee satellieten
Iran lanceert komende dagen twee satellieten 1 + 1 is niet gelijk aan 2 voor grafeenachtige 2D-materialen
1 + 1 is niet gelijk aan 2 voor grafeenachtige 2D-materialen Investeren in Australische wijnen
Investeren in Australische wijnen Het bijwonen van de beste middelbare school kan voordelen en risico's opleveren voor studenten
Het bijwonen van de beste middelbare school kan voordelen en risico's opleveren voor studenten Kleine gouden kogels kunnen asbestgerelateerde kankers helpen aanpakken
Kleine gouden kogels kunnen asbestgerelateerde kankers helpen aanpakken
- Elektronica
- Biologie
- Zonsverduistering
- Wiskunde
- French | Italian | Spanish | Portuguese | Swedish | German | Dutch | Danish | Norway |

-
Wetenschap © https://nl.scienceaq.com

