
Wetenschap
Optimale kwantumberekening gekoppeld aan zwaartekracht

Krediet:Anni Roenkae, pexels.com
Informatie en zwaartekracht lijken misschien totaal verschillende dingen, maar één ding hebben ze gemeen:ze kunnen allebei worden beschreven in het kader van de geometrie. Voortbouwend op deze verbinding, een nieuw artikel suggereert dat de regels voor optimale kwantumberekening worden bepaald door de zwaartekracht.
Natuurkundigen Paweł Caputa aan de Universiteit van Kyoto en Javier Magan aan het Instituto Balseiro, Centro Atómico de Bariloche in Argentinië heeft hun paper over het verband tussen quantum computing en zwaartekracht gepubliceerd in een recent nummer van Fysieke beoordelingsbrieven .
Op het gebied van computationele complexiteit, een van de belangrijkste ideeën is het minimaliseren van de kosten (in termen van rekenkracht) om een probleem op te lossen. In 2006, Michael Nielsen toonde aan dat, wanneer bekeken in de context van differentiële meetkunde, rekenkosten kunnen worden geschat op afstand. Dit betekent dat het minimaliseren van rekenkosten gelijk staat aan het vinden van minimale "geodeten, " wat de kortst mogelijke afstanden zijn tussen twee punten op een gekromd oppervlak.
Aangezien dit geometrische perspectief erg lijkt op de concepten die worden gebruikt om de zwaartekracht te beschrijven, De resultaten van Nielsen hebben ertoe geleid dat onderzoekers mogelijke verbanden tussen computationele complexiteit en zwaartekracht hebben onderzocht. Maar het werk is uitdagend, en onderzoekers proberen nog steeds basisvragen te achterhalen, zoals hoe "complexiteit" te definiëren in holografische modellen met betrekking tot kwantumzwaartekracht, vooral, conforme veldentheorie. Momenteel zijn er veel verschillende voorstellen om de basis op dit gebied te leggen.
Het belangrijkste doel van het nieuwe artikel is om deze verschillende ideeën samen te brengen door een universele beschrijving van complexiteit voor te stellen die slechts afhangt van een enkele grootheid (centrale lading). Dit leidt tot het ontdekken van verbanden tussen complexiteit en concepten in (kwantum)zwaartekracht die, beurtelings, leidt tot interessante implicaties, zoals de mogelijkheid dat zwaartekracht de regels bepaalt voor optimale kwantumberekening.
"Onlangs, kwantumberekeningstheoretici (waaronder Nielsen) brachten het idee naar voren dat de complexiteit van kwantumcircuits kan worden geschat door de lengte van de kortste geodeet in de 'complexiteitsgeometrie van unitaire transformaties, '" vertelde Caputa aan Phys.org . “Dat hebben we laten zien, in tweedimensionale conforme veldtheorieën met kwantumpoorten gegeven door de energie-impulstensor, de 'lengte' van dergelijke geodeten wordt berekend door (de werking van) tweedimensionale zwaartekracht.
"Het vinden van de minimale lengte op de complexiteitsgeometrie, in onze opstelling, is gelijk aan het oplossen van de zwaartekrachtsvergelijkingen. Dit is wat we bedoelden met regels voor het instellen van zwaartekracht voor optimale berekeningen in 2-D conforme veldtheorieën."
Dit perspectief suggereert dat zwaartekracht nuttig kan zijn bij het inschatten van de complexiteit van de computer en het identificeren van de meest efficiënte rekenmethoden voor het oplossen van problemen.
"Het begrip complexiteit van een bepaalde taak vertelt ons hoe moeilijk het is om het uit te voeren met onze beschikbare tools, "Zei Magan. "In de kwantumtheorie van berekeningen, dit idee wordt gegeneraliseerd naar de complexiteit van kwantumcircuits die zijn opgebouwd uit kwantumpoorten. Het inschatten ervan is over het algemeen een moeilijk probleem.
"We hebben aangetoond dat er families van kwantumsystemen zijn waar de complexiteit van bepaalde universele taken goed wordt geschat met behulp van klassieke zwaartekracht (algemene relativiteit). In de loop der jaren, gebruikmakend van holografie en Anti-de Sitter/conforme veldtheorieën, we hebben geleerd dat zwaartekracht nauw verbonden is met kwantuminformatie. De les van onze bevindingen is dat de zwaartekracht ons ook kan leren hoe we kwantumberekeningen in fysieke systemen op de meest efficiënte manier kunnen uitvoeren."
© 2019 Wetenschap X Netwerk
 Realisatie van kleurfiltervrije beeldsensoren
Realisatie van kleurfiltervrije beeldsensoren Meten van de verwijdering van plastic deeltjes uit het lichaam bij muizen
Meten van de verwijdering van plastic deeltjes uit het lichaam bij muizen Chemici ontdekken nieuwe kenmerken om cystische fibrose bij zuigelingen eerder te identificeren
Chemici ontdekken nieuwe kenmerken om cystische fibrose bij zuigelingen eerder te identificeren Nieuwe nikkelkatalysator werkt in water om broeikasgas om te zetten in chemische grondstof
Nieuwe nikkelkatalysator werkt in water om broeikasgas om te zetten in chemische grondstof De alkaliteit in een zoetwateraquarium verhogen
De alkaliteit in een zoetwateraquarium verhogen
 Nieuwe studie onthult verband tussen klimaat, leven en de beweging van continenten
Nieuwe studie onthult verband tussen klimaat, leven en de beweging van continenten Goudwinning met kwik levert kilometers stroomafwaarts gezondheidsrisico's op
Goudwinning met kwik levert kilometers stroomafwaarts gezondheidsrisico's op Hoe we ontdekten dat een asteroïdebotsing in de ruimte 466 miljoen jaar geleden het leven op aarde een boost gaf
Hoe we ontdekten dat een asteroïdebotsing in de ruimte 466 miljoen jaar geleden het leven op aarde een boost gaf 2020-emissies:precedent scheppen of tegen de trend in?
2020-emissies:precedent scheppen of tegen de trend in? Verschillende soorten alligators
Verschillende soorten alligators
Hoofdlijnen
- Waarom zijn er geen zeeslangen in de Atlantische Oceaan?
- Drones gebruiken om gewasschade door wilde zwijnen in te schatten
- Onderzoek naar superstil gemaakte DNA hints naar nieuwe manieren om cellen te herprogrammeren
- Teams Advance maakt het bewerken van genen met chirurgische precisie mogelijk
- Hoe worden nieuwe cellen geproduceerd?
- Hoe te lezen Proteïne elektroforese
- Hoe ribosomen het proteoom vormen
- Wat zijn de belangrijkste functies van microtubules in de cel?
- UVB-straling beïnvloedt het gedrag van stekelbaarzen
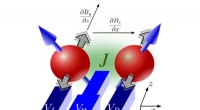
- Onderzoekers demonstreren met succes een kwantumpoort in silicium
- Systeem om het menselijk oog in beeld te brengen corrigeert voor chromatische aberraties

- Wetenschappers krijgen een ongekend beeld van bestraalde splijtstof

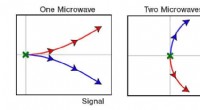
- Een snellere methode om kwantumgeheugen te lezen
- Neutronenclusteringseffect in kernreactoren voor het eerst aangetoond

 Studenten brengen zestig jaar data tot leven op het web
Studenten brengen zestig jaar data tot leven op het web Machine learning gaat dieper in op katalysatorinteracties om de ontwikkeling van materialen te versnellen
Machine learning gaat dieper in op katalysatorinteracties om de ontwikkeling van materialen te versnellen Techniek versterkt gebouwen met houtafval
Techniek versterkt gebouwen met houtafval Uit nieuw onderzoek blijkt dat mensen Twitter gebruiken om politieke scheidslijnen te overbruggen
Uit nieuw onderzoek blijkt dat mensen Twitter gebruiken om politieke scheidslijnen te overbruggen Studie brengt nanobody-structuur in kaart, wat leidt tot nieuwe manieren om mogelijk ziekten te bestrijden
Studie brengt nanobody-structuur in kaart, wat leidt tot nieuwe manieren om mogelijk ziekten te bestrijden Onderzoekers vinden kritieke beveiligingsfouten in AMD-chips
Onderzoekers vinden kritieke beveiligingsfouten in AMD-chips Er is een betere manier ontwikkeld om de aanwas van het superzware zwarte gat in het centrum van de Melkweg te simuleren
Er is een betere manier ontwikkeld om de aanwas van het superzware zwarte gat in het centrum van de Melkweg te simuleren Wachten op een onderzeese robot in Antarctica om naar huis te bellen
Wachten op een onderzeese robot in Antarctica om naar huis te bellen
- Elektronica
- Biologie
- Zonsverduistering
- Wiskunde
- French | Italian | Spanish | Portuguese | Swedish | German | Dutch | Danish | Norway |

-
Wetenschap © https://nl.scienceaq.com

