Wetenschap
Rationalisatie van fonondispersie:een efficiënte en nauwkeurige voorspelling van de thermische geleidbaarheid van het rooster
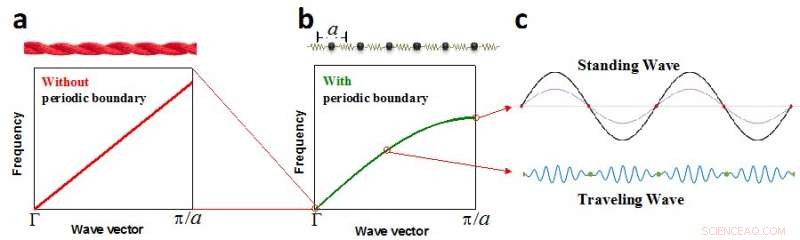
(a) lineaire fonon-dispersie op basis van akoestisch-elastische golfaanname, (b) sinus fonon-dispersie gezien de periodieke randvoorwaarde, (c) rooster staande golf (boven) en lopende golf (onder). Krediet:Science China Press
De thermische geleidbaarheid van roosters heeft een sterke invloed op de toepassingen van materialen die verband houden met thermische functionaliteit, zoals thermisch beheer, thermische barrièrecoatings en thermo-elektriciteit. Om de thermische geleidbaarheid van het rooster meer kwantitatief en op een tijd- en kosteneffectieve manier te begrijpen, veel onderzoekers hebben hun inspanningen gewijd en een paar fysieke modellen ontwikkeld met behulp van benaderde fonon-dispersies in de afgelopen eeuw.
De meeste van deze modellen gebruiken een lineaire fonon-dispersie, voorgesteld door Debye in 1912 op basis van een akoestisch-elastische golfaanname (figuur 1a), terwijl andere modellen ofwel aanpassingsparameters op fonon-dispersie omvatten of gedetailleerde vergelijkingen voor fonon-transporteigenschappen missen. De lineaire fonondispersie van Debye biedt veel vereenvoudigingen op fonontransporteigenschappen, en was de meest voorkomende benadering in de afgelopen eeuw. De lineaire dispersie van Debye voorspelt met succes de T3-afhankelijkheid van de warmtecapaciteit bij zeer lage temperaturen, en warmtecapaciteit nadert de Dulong-Petit-limiet bij hoge temperaturen. Echter, de aard van periodiciteit op atomaire rangschikkingen leidt tot een periodieke randvoorwaarde voor roostertrillingen in vaste stoffen (figuur 1b), die in feite staande roostergolven creëert aan de grenzen van Brillouin (figuur 1c). Dit voldoet niet aan de akoestisch-elastische golfaanname van Debye, zoals voorgesteld door Born en von Karman (BvK) in 1912 - hetzelfde jaar dat Debye de lineaire dispersie voorstelde.
Dit resulteert in een significante afwijking van Debye-dispersie voor periodieke kristallijne materialen wanneer fononen met golfvectoren zich dicht bij de Brillouin-grenzen (hoogfrequente fononen) bevinden. Wanneer deze fononen worden gebruikt voor fonontransport (d.w.z. bij niet extreem lage temperaturen), Debye-dispersie leidt tot een overschatting van de thermische geleidbaarheid van het rooster vanwege de overschatting van de groepssnelheid voor deze hoogfrequente fononen, zoals waargenomen in materialen met honderden bekende gemeten roosterwarmtegeleidingsvermogen en noodzakelijke details voor een tijd- en kosteneffectieve modelvoorspelling voor zover wij weten (Fig. 2g en h tonen een gemiddelde absolute afwijking van ~ + 40%). In aanvulling, Debye-dispersie overschat ook de theoretisch beschikbare ondergrens van de thermische geleidbaarheid van het rooster, waardoor de schendingen van de gemeten thermische geleidbaarheid van het rooster zelfs lager zijn dan het huidige theoretische minimum voorspeld (gebaseerd op het Debye-Cahill-model), zoals waargenomen in tientallen materialen.
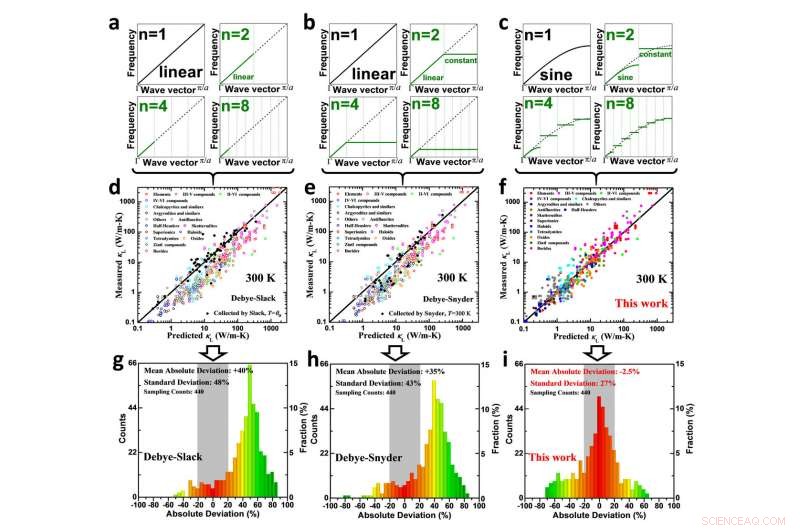
Vergelijking op fonondispersie (a, b en c), gemeten rooster thermische geleidbaarheid versus voorspelling (d, e en f) en de bijbehorende foutenanalyses (g, h en i) voor Debye-Slack-model (a, d en g), Debye-Snyder-model (b, e en h) en degene die in dit werk is ontwikkeld gezien de periodieke randvoorwaarde (c, g en i) voor kristallijne vaste stoffen. Krediet:Science China Press
Dit werk houdt rekening met de BvK-randvoorwaarde, en onthult dat het product van akoestische en optische dispersies een sinusfunctie oplevert. In het geval waarvan de massa (of de krachtconstante) contrast tussen atomen groot is, de akoestische dispersie heeft de neiging een sinusfunctie te zijn. Deze dispersie van het sinustype bestaat inderdaad in zowel de eenvoudigste als de meest complexe materialen. Benadering van de akoestische dispersie als sinus, de BvK-randvoorwaarde reduceert vervolgens de resterende optische takken tot een reeks gelokaliseerde modi met een reeks constante frequenties. Terwijl eerste-principeberekeningen een meer gedetailleerde fonon-dispersie mogelijk maken, een ontwikkeling van gerationaliseerde fonon-dispersie voor een tijd- en kosteneffectieve voorspelling van fonon-transport is belangrijk vanwege het tijdrovende en rekenkundige dure voor eerste-principe berekeningen.
Dit werk maakt gebruik van de bovengenoemde rationalisatie van fonon-dispersies, waardoor beide bijdragen aan de thermische geleidbaarheid van akoestische en optische fononen kunnen worden opgenomen. Deze verbetering in fonon-dispersies verbetert de nauwkeurigheid van een tijd- en kosteneffectieve voorspelling van de roosterwarmtegeleiding van vaste stoffen aanzienlijk zonder enige passende parameters (figuur 2c, met een gemiddelde absolute afwijking van slechts -2,5%), en biedt daarom een nauwkeuriger ontwerp van vaste stoffen met verwachte rooster thermische geleidbaarheid. Verder, dit werk verwijdert met succes de tegenstrijdigheid dat de gemeten thermische geleidbaarheid van het rooster zelfs lager is dan het theoretische minimum dat voorspeld is op basis van een lineaire dispersie van Debye (Fig. 3). Dit zou de theoretische mogelijkheid bieden om de thermische geleidbaarheid van het rooster lager te maken dan momenteel wordt gedacht, het openen van verdere mogelijkheden voor het bevorderen van thermisch resistente materialen voor toepassingen, inclusief thermo-elektriciteit.
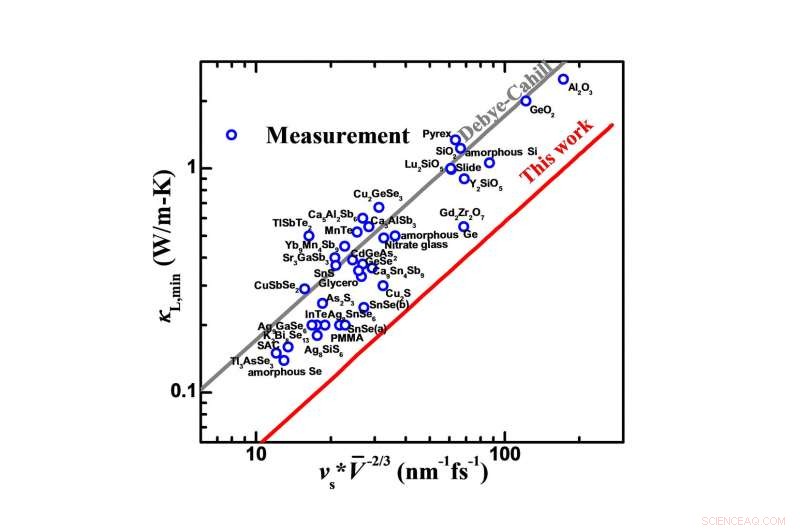
Vergelijking op gemeten minimale rooster thermische geleidbaarheid (?L, min) en voorspellingen gebaseerd op een spreiding ontwikkeld volgens de periodieke randvoorwaarde of op een lineaire spreiding van Debye (Debye-Cahill model). Krediet:Science China Press
 Wetenschappers ontwikkelen sondes die zijn ontworpen om de fysieke krachten in levende cellen te onthullen; een wereldprimeur
Wetenschappers ontwikkelen sondes die zijn ontworpen om de fysieke krachten in levende cellen te onthullen; een wereldprimeur Wetenschappers ontwikkelen diagnostische test die erop gericht is antibioticaresistentie in minder dan 45 minuten op te sporen
Wetenschappers ontwikkelen diagnostische test die erop gericht is antibioticaresistentie in minder dan 45 minuten op te sporen Wetenschappers ontdekken nieuwe architectuur in maïs
Wetenschappers ontdekken nieuwe architectuur in maïs Onderzoekers ontwerpen sensoren om plantenhormonen snel te detecteren
Onderzoekers ontwerpen sensoren om plantenhormonen snel te detecteren Hoe maak je een zelfgemaakte match
Hoe maak je een zelfgemaakte match
 Overstromingen en modderstromen dragen bij aan St. Vincents vulkaanproblemen
Overstromingen en modderstromen dragen bij aan St. Vincents vulkaanproblemen Nieuw rapport bekijkt hoe andere landen hun land beheren
Nieuw rapport bekijkt hoe andere landen hun land beheren De COVID-lockdown in China heeft het aantal ziekenhuisopnames in verband met luchtvervuiling aanzienlijk verminderd
De COVID-lockdown in China heeft het aantal ziekenhuisopnames in verband met luchtvervuiling aanzienlijk verminderd Menselijk gedrag moet worden meegenomen in analyses van klimaatverandering
Menselijk gedrag moet worden meegenomen in analyses van klimaatverandering In de Middellandse Zee woeden bosbranden. Wat kunnen we leren?
In de Middellandse Zee woeden bosbranden. Wat kunnen we leren?
Hoofdlijnen
- Houden mannelijke vissen ze liever groot en kleurrijk?
- Dierentuin Praag viert gezondheid zeldzame Maleise tijgerwelpen
- Voordelen en nadelen van Hydrostatic Skeleton
- Los Angeles Zoos oude Indiase neushoorn geëuthanaseerd
- Welke pakketten materialen van het endoplasmatisch reticulum en verzendt ze naar andere delen van de cel?
- Mendelian Vs. Moderne genetica
- Berekening van de tijd voor celverdubbeling
- Wat is opsomming in de microbiologie?
- Transcriptiefactoren en genexpressie heroverwegen
 Oude vulkaanuitbarstingen verstoorden de thermostaat van de aarde, een sneeuwbalplaneet creëren
Oude vulkaanuitbarstingen verstoorden de thermostaat van de aarde, een sneeuwbalplaneet creëren Onderzoekers maken een kleine laser met behulp van nanodeeltjes
Onderzoekers maken een kleine laser met behulp van nanodeeltjes Team achter 's werelds eerste afbeelding van een zwart gat wint Oscar voor wetenschap
Team achter 's werelds eerste afbeelding van een zwart gat wint Oscar voor wetenschap Niet alle theorieën kunnen het zwarte gat M87* verklaren
Niet alle theorieën kunnen het zwarte gat M87* verklaren Een zomer van leren, diep in Costa Rica
Een zomer van leren, diep in Costa Rica Polluties Gevolgen voor historische monumenten
Polluties Gevolgen voor historische monumenten Microscopisch Lego om wetenschappers de komende 50 jaar bezig te houden
Microscopisch Lego om wetenschappers de komende 50 jaar bezig te houden Elektrotechnisch team ontwikkelt verder dan 5G draadloze transceiver
Elektrotechnisch team ontwikkelt verder dan 5G draadloze transceiver
- Elektronica
- Biologie
- Zonsverduistering
- Wiskunde
- French | Italian | Spanish | Portuguese | Swedish | German | Dutch | Danish | Norway |

-
Wetenschap © https://nl.scienceaq.com