
Wetenschap
Nieuwe 3D-structuur toont optimale manier om ruimte in te delen
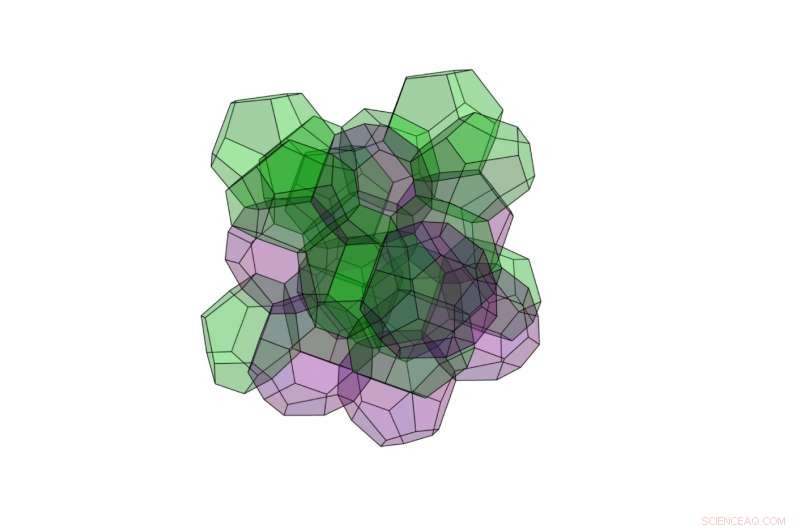
Een van de nieuwe 3D-structuren heeft het laagste oppervlak van alle bekende ruimtescheidingsstructuren:het is gemaakt van 24 veelvlakken, waarvan sommige 12 gezichten hebben en sommige 16 gezichten. Omdat de veelvlakken met 12 en 16 gezichten hier verschillende volumes hebben, de nieuwe structuur voldoet niet aan de oorspronkelijke eis van Kelvin voor gelijke volumes. Krediet:Opsomer en Vandewalle. ©2016 IOP Publishing
(Phys.org)—Onderzoekers hebben een nieuwe 3D-structuur ontdekt die de ruimte in 24 regio's verdeelt, en hebben aangetoond dat het de beste oplossing tot nu toe is voor een aangepaste versie van een geometrisch ruimteverdelingsprobleem dat onderzoekers al meer dan een eeuw uitdaagt.
In 1887, Lord Kelvin vroeg hoe de ruimte kan worden opgedeeld in 3D-structuren van gelijk volume op een manier die het totale oppervlak van elke structuur minimaliseert. Het moet mogelijk zijn om veel van deze structuren stevig samen te voegen zonder gaten ertussen - met andere woorden, het moeten "ruimtevullende" structuren zijn. Elke structuur kan verschillende complexe 3D-vormen aannemen, of "veelvlakken, " ofwel als een enkel veelvlak of een combinatie van meerdere kleinere veelvlakken van verschillende typen. De uitdaging is om erachter te komen welke specifieke soorten veelvlakken moeten worden gebruikt om het buitenoppervlak van de hele structuur te minimaliseren.
Kelvins beste oplossing voor dit probleem was een enkelvoudig veelvlak genaamd een "tetrakaidecaëder, " die 14 vlakken heeft:zes vierkanten en acht zeshoeken. Aangezien dit de vorm is die wordt verkregen bij het afsnijden van de hoeken van een 3D-diamantvorm, het kan ook worden gezien als een afgeknotte octaëder.
Hoewel de oplossing van Kelvin meer dan een eeuw standhield, in 1994 gebruikten Denis Weaire en Robert Phelan van Trinity College Dublin numerieke simulaties om een meer optimale ruimteverdeling te ontdekken. De oplossing van Weaire en Phelan bestaat uit acht veelvlakken van twee verschillende typen, hoewel beide typen hetzelfde volume hebben:zes tetrakaidecaëders van Kelvin en twee dodecaëders (die 12 vlakken heeft). Samen, deze acht veelvlakken vormen een 3D-structuur die 0,3% minder oppervlakte heeft dan de enkele tetrakaidecaëder van Kelvin. De Weaire-Phelan-structuur is de afgelopen 22 jaar de meest optimale oplossing voor het probleem van Kelvin gebleven.
Nu in de nieuwe studie, natuurkundigen Eric Opsomer en Nicolas Vandewalle van de Universiteit van Luik in België hebben een nieuw algoritme ontwikkeld voor het vinden van ruimtevullende composiet polyedrische structuren met een minimaal oppervlak.
Met behulp van de nieuwe methode, ze ontdekten dat een nieuwe 3D-structuur gemaakt van 24 veelvlakken een nog kleiner oppervlak heeft dan de Weaire-Phelan-structuur. De 24 veelvlakken zijn van twee verschillende typen:sommige hebben 12 gezichten en sommige hebben 16 gezichten. In tegenstelling tot de Weaire-Phelan-structuur, waarin de twee verschillende soorten veelvlakken gelijke volumes hebben, de 12- en 16-faced veelvlakken hebben hier significant verschillende volumes. Om deze reden, de nieuwe structuur voldoet niet aan de oorspronkelijke eis van Kelvin voor gelijke volumes.
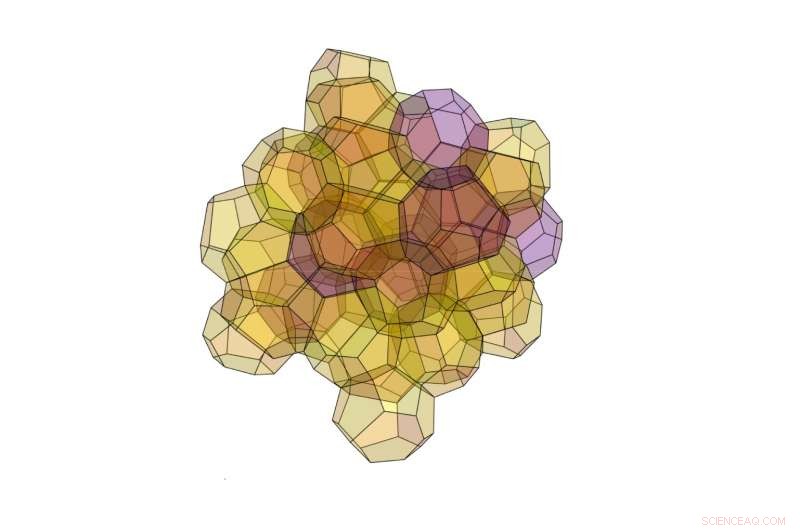
Het nieuwe algoritme onthulde deze 3D-structuur die bestaat uit 40 veelvlakken van twee verschillende typen. Krediet:Opsomer en Vandewalle. ©2016 IOP Publishing
"Helaas, het is geen 'echte oplossing, ' aangezien cellen met een gelijk volume een vereiste zijn voor het oorspronkelijke Kelvin-probleem, "Opsomer vertelde" Phys.org . Niettemin, de structuur is om andere redenen nog steeds interessant. "Deze resultaten kunnen leiden tot de ontdekking van structuren met mogelijke implicaties voor de materiaalfysica, medisch onderzoek, en andere gebieden, ' zei Opsomer.
Zoals de onderzoekers uitlegden, ze hebben opzettelijk de beperking van gelijke volumes verwijderd bij het ontwikkelen van hun zoekmethode, omdat het hen in staat stelde het algoritme op een nieuwe manier te ontwerpen:in plaats van het oppervlak van een structuur direct te minimaliseren, ze maximaliseerden de gemiddelde isoperimeters van de veelvlakken (de omtrekken gedeeld door alle aangrenzende veelvlakken). Hoewel deze twee benaderingen verschillend zijn, ze zijn uiteindelijk gelijkwaardig.
De onderzoekers gebruikten het nieuwe algoritme om verschillende 3D-structuren te verkennen die bestaan uit twee tot 64 veelvlakken. Beginnend met een specifiek aantal willekeurig gerangschikte punten in de 3D-ruimte, het algoritme begint de punten te verplaatsen. Na elke iteratie, het algoritme berekent de nieuwe gemiddelde isoperimeter, en op basis van het resultaat behoudt of verwerpt u de nieuwe configuratie met een bepaalde waarschijnlijkheid. Na miljoenen en soms miljarden iteraties, de punten vormen uiteindelijk de hoekpunten van meerdere veelvlakken die samen een 3D-structuur vormen met een zeer klein oppervlak.
Aangezien er momenteel geen manier is om te bewijzen wat de meest optimale ruimteverdelingsstructuur is (met of zonder cellen van gelijk volume), de onderzoekers zijn van plan om door te gaan met het doorzoeken van een grote verscheidenheid aan structuren van alle soorten. Hun beste gok is dat er nog meer optimale structuren bestaan, en ze zijn van plan hun algoritme te gebruiken om hun verkenning voort te zetten.
De onderzoekers verwachten ook dat het algoritme andere unieke structuren kan genereren. Een bijzonder interessante structuur die ze hier ontdekten, is een structuur met 40 veelvlakken die meer optimaal is dan de structuur van Kelvin, maar niet zo goed als de Weaire-Phelan-structuur. Deze zeer complexe structuur is ook ongebruikelijk omdat het niet behoort tot een categorie van structuren die Frank-Kasper-structuren worden genoemd, waar onderzoekers zich traditioneel op hebben gericht voor optimale ruimteverdeling. De bevinding suggereert dat er ook andere optimale structuren kunnen bestaan buiten deze categorie.
Hoewel het probleem van Kelvin oorspronkelijk niet werd voorgesteld om aan een praktische behoefte te voldoen, optimale ruimteverdeling heeft nu een verscheidenheid aan toepassingen. Op medisch gebied, deze concepten zijn gebruikt om sterke, lichtgewicht botweefselvervangingen. Optimale ruimteverdeling heeft ook de architectuur geïnspireerd, met als opmerkelijk voorbeeld de zwemlocatie die is gebouwd voor de Olympische Spelen van 2008 in Peking. Het gebouw, die de waterkubus wordt genoemd, is gebaseerd op de Weaire-Phelan-structuur.
© 2016 Fys.org
 Een nieuwe klasse antibioticakandidaten voor de bestrijding van superbacteriën
Een nieuwe klasse antibioticakandidaten voor de bestrijding van superbacteriën Wetenschappers ontrafelen synthetisch mechanisme van arylpentazol en substituenteffect
Wetenschappers ontrafelen synthetisch mechanisme van arylpentazol en substituenteffect Zes soorten kristallijne vaste stoffen
Zes soorten kristallijne vaste stoffen Bewijsstuk A en andere echte misdaadshows kunnen misvattingen over forensische wetenschap aanwakkeren
Bewijsstuk A en andere echte misdaadshows kunnen misvattingen over forensische wetenschap aanwakkeren Joules converteren naar Kelvin
Joules converteren naar Kelvin
 Het plantenleven breidt zich uit in de Everest-regio
Het plantenleven breidt zich uit in de Everest-regio NASA-satelliet toont tyfoon Mitags groot bereik boven Oost-Chinese Zee
NASA-satelliet toont tyfoon Mitags groot bereik boven Oost-Chinese Zee Ambtenaren:CO2-afvangproject zou het grootste ter wereld zijn
Ambtenaren:CO2-afvangproject zou het grootste ter wereld zijn Tyfoon raast Japan binnen, nadert door rampen getroffen regio's
Tyfoon raast Japan binnen, nadert door rampen getroffen regio's insecten, ziekte verwoest bomen in Zuid-Californië. Wie gaat ze stoppen?
insecten, ziekte verwoest bomen in Zuid-Californië. Wie gaat ze stoppen?
Hoofdlijnen
- Ja,
- Welke materialen kan ik gebruiken om een DNA-model te maken?
- Wetenschappers ontwerpen bacteriën om sonarsignalen te reflecteren voor ultrasone beeldvorming
- Hoeveel spieren heb je nodig om te glimlachen?
- Chimpansees bleken arm- en monduitdrukkingen te gebruiken om afstand over te brengen
- Afbrekende koraalriffen slecht nieuws voor commerciële visserij
- Wat is celcompartimentering en waarom doet het zich voor?
- Een stap dichter bij gewassen met twee keer de opbrengst
- De rol van de longen
- Geïnspireerd door regenwormen, nieuw ademend materiaal smeert zichzelf indien nodig

- Natuurkundigen gebruiken terahertz-flitsen om de toestand van materie te ontdekken die verborgen is door supergeleiding

- Een sterrenbeeldmodel voor een schoolproject

- Indeterministische fysica voor een open wereld

- Licht berekent elke gewenste lineaire transformatie zonder een digitale processor

 Een psychologische benadering van mens-automatisering interactie
Een psychologische benadering van mens-automatisering interactie Magnets uitleggen aan Kindergarteners
Magnets uitleggen aan Kindergarteners Radiotelescoop registreert een zeldzame storing in een pulsars regelmatige pulserende beat
Radiotelescoop registreert een zeldzame storing in een pulsars regelmatige pulserende beat Nieuw productieproces creëert superkleine kanalen om water af te weren en medische, elektronische apparaten
Nieuw productieproces creëert superkleine kanalen om water af te weren en medische, elektronische apparaten Achtertuin niet achterlijk:opzettelijk leven, de opkomst van imikhukhu en stedelijke verdichting voor waardigheid
Achtertuin niet achterlijk:opzettelijk leven, de opkomst van imikhukhu en stedelijke verdichting voor waardigheid Werktuigbouwkunde op moleculair niveau:zelfassemblage van nano-rotors (met video)
Werktuigbouwkunde op moleculair niveau:zelfassemblage van nano-rotors (met video) Ambae vulkanen kratermeren maken het een ernstige bedreiging voor Vanuatu
Ambae vulkanen kratermeren maken het een ernstige bedreiging voor Vanuatu Copernicus 20 jaar later
Copernicus 20 jaar later
- Elektronica
- Biologie
- Zonsverduistering
- Wiskunde
- French | Italian | Spanish | Portuguese | Swedish | German | Dutch | Danish | Norway |

-
Wetenschap © https://nl.scienceaq.com

