
Wetenschap
Wat wordt bedoeld met de de Broglie -golflengte van een deeltje?
Key Concepts:
* Dualiteit van golfdeeltjes: De hypothese van de Broglie breidde het dualiteitsconcept van de golfdeeltjes uit (al vastgesteld voor licht) om ertoe te doen. Hij stelde voor dat alle materie golfachtige eigenschappen vertoont.
* Momentum: Het momentum van een deeltje is een maat voor zijn massa en snelheid. Het is een vectorhoeveelheid (met zowel grootte als richting).
* golflengte: Golflengte is de afstand tussen twee opeenvolgende toppen of dalen van een golf.
formule:
De de Broglie -golflengte (λ) van een deeltje wordt gegeven door:
`` `
λ =h / p
`` `
waar:
* λ is de de Broglie -golflengte
* h is de constante van Planck (6.626 x 10⁻³⁴ j · s)
* p is het momentum van het deeltje (massa * snelheid)
Betekenis:
De de Broglie -golflengte helpt ons te begrijpen:
* Wave-achtig gedrag van materie: Het verklaart waarom deeltjes zoals elektronen diffractie en interferentiepatronen kunnen vertonen, net als golven.
* kwantumkarakter van materie: Het onthult dat het gedrag van deeltjes op atoom- en subatomaire niveau niet alleen door de klassieke fysica kan worden verklaard en kwantummechanica vereist.
* Toepassingen: Het concept van de Broglie heeft belangrijke toepassingen op velden zoals:
* Elektronenmicroscopie: Het gebruik van de golfachtige aard van elektronen om afbeeldingen met hoge resolutie te maken.
* Quantum computing: Gebruikmakend van de golfeigenschappen van deeltjes voor berekening.
Voorbeeld:
Overweeg een elektron met een momentum van 1,0 x 10⁻²⁴ kg · m/s. De de Broglie -golflengte zou zijn:
`` `
λ =(6.626 x 10⁻³⁴ j · s) / (1,0 x 10⁻²⁴ kg · m / s) =6.626 x 10⁻¹⁰ m m
`` `
Deze golflengte valt binnen het bereik van röntgenfoto's, wat de golfachtige aard van elektronen op dit momentum aangeeft.
Belangrijke opmerking: De de Broglie -golflengte wordt alleen significant op zeer kleine schalen (atomaire en subatomaire niveaus). Voor macroscopische objecten is de golflengte extreem klein en praktisch niet detecteerbaar.
 Kan een drone de duistere geheimen van de Baai van San Francisco onthullen?
Kan een drone de duistere geheimen van de Baai van San Francisco onthullen? Sommige keukenkasten kunnen mogelijk schadelijke stoffen uitstoten
Sommige keukenkasten kunnen mogelijk schadelijke stoffen uitstoten Microscopische defecten in het ijs beïnvloeden de manier waarop enorme gletsjers stromen, zo blijkt uit onderzoek
Microscopische defecten in het ijs beïnvloeden de manier waarop enorme gletsjers stromen, zo blijkt uit onderzoek  Wat is de creatie?
Wat is de creatie?  Wat is de zone van stilte?
Wat is de zone van stilte?
Hoofdlijnen
- Bsal en verder:Taskforce helpt de dreiging van amfibieënziekten af te wenden
- Te veel voertuigen, trage reacties en roekeloos samenvoegen:nieuw wiskundig model legt uit hoe verkeersbacteriën bewegen
- Ontdekking van oud glasvezelfossiel uit Glasgow onthult nieuwe soorten
- Wat betekent BIOTC?
- Wat eronder ligt:de groei van wortelcellen is opmerkelijk dynamisch, zo blijkt uit onderzoek
- Waarom kunnen twee wetenschappers dezelfde gegevens bestuderen, maar komen ze tot verschillende conclusies?
- Vergelijking voor glucosemetabolisme
- Wat is het opslagcentrum van een dierlijke cel?
- Neushoornstroper krijgt 20 jaar cel in Zuid-Afrika
- Klimaatvriendelijke schuimisolatie van gebouwen kan meer kwaad dan goed doen

- Ingenieurs ontwikkelen kameleonmetalen die van oppervlak veranderen als reactie op hitte
- Hoe interageren metalen met DNA?
- Nieuwe krachtige analogen van plantenhormoon zorgen voor verlichting van droogtestress voor gewassen
- Replicatie van extract van mangosteenschil als behandeling voor darmontsteking bij mens en dier
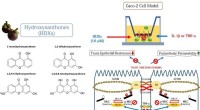
 Deense onderzoekers creëren wereldwijd model voor zonne-energie
Deense onderzoekers creëren wereldwijd model voor zonne-energie Welke laag van de aarde vormt aardplaten?
Welke laag van de aarde vormt aardplaten?  Zou KB voor een zwakke basis op dezelfde manier kunnen worden bepaald als kazuur wordt bepaald?
Zou KB voor een zwakke basis op dezelfde manier kunnen worden bepaald als kazuur wordt bepaald?  Hoe goed zijn testen op E. coli in beken?
Hoe goed zijn testen op E. coli in beken?  Hoe ver onder het aardoppervlak zou je eerder moeten gaan.
Hoe ver onder het aardoppervlak zou je eerder moeten gaan.  Welk terrestrisch bioom is misschien warm of koud, maar heeft altijd een kleine neerslag?
Welk terrestrisch bioom is misschien warm of koud, maar heeft altijd een kleine neerslag?  Waarom groep 4 metalen vormen ionen?
Waarom groep 4 metalen vormen ionen?  Lessen over klimaatverandering uit Afrika:kennis is de sleutel
Lessen over klimaatverandering uit Afrika:kennis is de sleutel
- Elektronica
- Biologie
- Zonsverduistering
- Wiskunde
- French | Italian | Spanish | Portuguese | Swedish | German | Dutch | Danish | Norway |

-
Wetenschap © https://nl.scienceaq.com

