
Wetenschap
Een monster van 50 ml van een oplossing van 1,00 ml cuso4 wordt gemengd met 2 m koh in een calorimeter. De temperatuur van beide oplossingen was 20,2 C vóór het mengen en 26,3 °C na het mengen?
Volgens de gegeven voorwaarde:
$$T_1=20,2^0 C$$
$$T_2=26,3 ^0 C$$
$$C_{CuSO_4}=50\ ml$$
$$M_{CuSO_4} =1,00\ mol/ml$$
$$V_{KOH}=2\ M$$
De warmteverandering $$(\Delta H)$$ van de reactie wordt gegeven als:
$$\Delta H =-C_pm_c\Delta T$$
Waar:
$$C_p=specifieke \ warmte \ constante\ van \ water$$
De soortelijke warmteconstante van water is $$4,184 J/g^0 C$$
$$m_c=massa\ van\ calorimeter\ oplossing$$
De dichtheid van water is $$1g/ml$$
Daarom massa van de oplossing=volume$$=50+50=100g$$
Dus $$m_c=100g$$
$$\Delta T=T_2-T_1=26,3-20,2=6,1 ^0C$$
Als we deze waarden in de bovenstaande uitdrukking vervangen, krijgen we
$$\Delta H=-(4,184\ J/g^0 C) \ (100g)( 6,1^0 C)$$
$$=-2567,94\ J$$
$$\dus \Delta H=-2,57\ kJ$$
De reactie-enthalpie is dus -2,57 kJ
 Wat zijn de voordelen van americium?
Wat zijn de voordelen van americium?  Wetenschappers onderzoeken racemasen en stellen strategieën voor om medicijnen te vinden die zich richten op deze belangrijke enzymen
Wetenschappers onderzoeken racemasen en stellen strategieën voor om medicijnen te vinden die zich richten op deze belangrijke enzymen Hoeveel atomen zitten er in gips Parijs?
Hoeveel atomen zitten er in gips Parijs?  'S Werelds langste flessenborstelpolymeer ooit gesynthetiseerd
'S Werelds langste flessenborstelpolymeer ooit gesynthetiseerd Parodontitis:onderzoekers zoeken naar een nieuwe werkzame stof
Parodontitis:onderzoekers zoeken naar een nieuwe werkzame stof
 NASA kijkt hoe de tropische storm Jose wordt georganiseerd
NASA kijkt hoe de tropische storm Jose wordt georganiseerd Hernieuwbare energie en de strijd om de Guatemalteekse rivieren
Hernieuwbare energie en de strijd om de Guatemalteekse rivieren De vervuilingsregels van Trump worden teruggedraaid om steenkoolland hard te raken
De vervuilingsregels van Trump worden teruggedraaid om steenkoolland hard te raken Waarom landbouwgroepen fel gekant zijn tegen de CO2-belasting
Waarom landbouwgroepen fel gekant zijn tegen de CO2-belasting Wetenschapsbeursideeën met paarden
Wetenschapsbeursideeën met paarden
Hoofdlijnen
- Heeft de jacht op trofeeën invloed op de evolutie van dikhoornschapen? Onderzoek zegt nee
- Aanpassing van het fotosynthesemechanisme in luchtplanten vindt plaats door middel van genduplicatie, zo blijkt uit onderzoek
- Nieuw ontdekt proces van seksuele voortplanting bevordert het begrip van de evolutie van planten en algen
- Onderzoekers brengen het menselijk genoom in 4-D in kaart terwijl het vouwt
- Waar is de kern gevonden in de cel en waarom?
- Jonge, koelbloedige dieren lijden het meest door de opwarming van de aarde, blijkt uit onderzoek
- Bestudeer details van strategieën voor succesvolle stedelijke boomplantinitiatieven
- Nieuw machine learning-systeem kan automatisch vormen van rode bloedcellen identificeren
- Wat doodt de Argentijnse walvissen?
- Afbeeldingen van onzichtbare gaten in cellen kunnen onderzoek op gang brengen

- Populair hulpmiddel voor het ontdekken van medicijnen is nu 10 keer sneller geworden

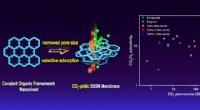
- Eenfasige covalente organische raamwerkmembranen maken CO2-selectieve scheiding mogelijk
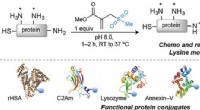
- Hoe een chemische kettingreactie aan te wakkeren?
- Onderzoekers bouwen een duurzame moleculaire coderingssleutel van sequentiegedefinieerde polymeren

 Groot-Brittannië publiceert langverwacht luchtvervuilingsplan
Groot-Brittannië publiceert langverwacht luchtvervuilingsplan Hoe word je een legerlinguïst
Hoe word je een legerlinguïst  Voor het volgen van een epidemie zijn computermodellen nodig, maar wat als die modellen niet kloppen?
Voor het volgen van een epidemie zijn computermodellen nodig, maar wat als die modellen niet kloppen?  COVID-19 dwingt universiteiten om over te schakelen naar online lessen, maar zijn ze er klaar voor?
COVID-19 dwingt universiteiten om over te schakelen naar online lessen, maar zijn ze er klaar voor? Nieuwe vaardigheden van grafeen:afstembare roostertrillingen
Nieuwe vaardigheden van grafeen:afstembare roostertrillingen Nanodeeltjes trainen immuuncellen om kanker te bestrijden
Nanodeeltjes trainen immuuncellen om kanker te bestrijden  Vraag ons allesWelke van de volgende is een voorbeeld van Arrhenius-zuur?
Vraag ons allesWelke van de volgende is een voorbeeld van Arrhenius-zuur?  Bescherming van breedband RF-systemen in overbelaste elektromagnetische omgevingen
Bescherming van breedband RF-systemen in overbelaste elektromagnetische omgevingen
- Elektronica
- Biologie
- Zonsverduistering
- Wiskunde
- French | Italian | Spanish | Portuguese | Swedish | German | Dutch | Danish | Norway |

-
Wetenschap © https://nl.scienceaq.com

