
Wetenschap
Wat is het verschil van natuurkunde?
Hier is een uitsplitsing van het concept en de toepassingen ervan:
1. Wat is een verschil?
* Infinitesimale verandering: Een differentieel vertegenwoordigt een oneindig kleine verandering in een variabele. Het wordt vaak aangeduid met "D" gevolgd door de variabele, zoals "DX" voor een kleine verandering in X.
* snelheid van verandering: Differentiëlen zijn nauw verwant met het concept van derivaten. De afgeleide van een functie vertelt ons de onmiddellijke snelheid van verandering van die functie ten opzichte van de invoervariabele.
2. Voorbeelden in de natuurkunde:
* Verplaatsing en snelheid: Als u een bewegend object heeft, verandert de positie (verplaatsing) in de loop van de tijd. Het differentieel van verplaatsing, "DX", vertegenwoordigt een kleine verandering in positie. Door deze verandering in positie te verdelen door de verandering in de tijd (DT), krijgt u de onmiddellijke snelheid:dx/dt =v.
* Force and Acceleration: Het differentieel van snelheid, "dv", vertegenwoordigt een kleine verandering in snelheid. Door deze verandering in snelheid te verdelen door de verandering in de tijd (DT), krijgt u de versnelling:dv/dt =a.
* werk en energie: Het werk dat op een object is gedaan, is gelijk aan de kracht die wordt toegepast, vermenigvuldigd door de afgelegde afstand. Als u een kleine verandering in verplaatsing "dx" en een kracht "f" hebt, "is het werk dat wordt gedaan over die kleine verplaatsing" f * dx ".
3. Belangrijkste toepassingen:
* Begaande beweging: Verschillen zijn essentieel voor het in detail beschrijven van beweging, omdat ze ons in staat stellen te analyseren hoe snelheid en versnelling in de loop van de tijd veranderen.
* Velden analyseren: Differentiëlen worden gebruikt in het begrijpen van velden zoals elektrische en magnetische velden, waarbij de veldsterkte over de ruimte verandert.
* Vergelijkingen oplossen: Veel fysieke vergelijkingen worden uitgedrukt met behulp van differentiëlen, zoals de tweede bewegingswet van Newton (F =MA). Om deze vergelijkingen op te lossen, gebruiken we calculustechnieken met verschillen.
Samenvattend:
Differentiëlen zijn een krachtig hulpmiddel in de natuurkunde, waardoor we de ingewikkelde relaties tussen fysieke hoeveelheden kunnen analyseren en hoe ze veranderen ten opzichte van elkaar. Ze zijn van fundamenteel belang voor het begrijpen van beweging, krachten, velden en vele andere aspecten van de fysieke wereld.
 Wat is de coëfficiënt van thermische expansie benzine?
Wat is de coëfficiënt van thermische expansie benzine?  Wat zijn de vier soorten metaal?
Wat zijn de vier soorten metaal?  Wat zijn enkele fysische eigenschappen van Berkelium?
Wat zijn enkele fysische eigenschappen van Berkelium?  Welke eigenschap zou u kunnen testen door het ene mineraal rechtstreeks tegen een ander mineraal te wrijven?
Welke eigenschap zou u kunnen testen door het ene mineraal rechtstreeks tegen een ander mineraal te wrijven?  Innovatieve verwerking en verpakking voor veilige, hoge kwaliteit, biologische bessenproducten
Innovatieve verwerking en verpakking voor veilige, hoge kwaliteit, biologische bessenproducten
 Is er fossiel bewijs voor de menselijke evolutie?
Is er fossiel bewijs voor de menselijke evolutie?  Overeenkomst van Parijs:vijf jaar later, het is tijd om de handel in koolstof op te lossen
Overeenkomst van Parijs:vijf jaar later, het is tijd om de handel in koolstof op te lossen Studie vindt organische bodemvangsten, houdt meer koolstof vast
Studie vindt organische bodemvangsten, houdt meer koolstof vast Hoe klaproosbloemen die levendige kleuren krijgen die insecten lokken
Hoe klaproosbloemen die levendige kleuren krijgen die insecten lokken  Italië's droogte gezien vanuit de ruimte
Italië's droogte gezien vanuit de ruimte
Hoofdlijnen
- Zijn zuur snelle bacteriën gram positief of negatief?
- Wat zijn de SAB-branches van de evolutiebiologie?
- Is het bevruchte ei een eencellulair organisme?
- Maak de functies van het celmembraan op de lijst?
- Welke witte bloedcellen produceren antilichamen en spelen een rol bij de immuunrespons?
- Welke soorten organen vormen het resortory -systeem?
- Wat bedoelen wetenschappers met mutaties zijn willekeurig?
- Een nieuwe strategie om cold case-onderzoeken te versnellen
- Wat is de verdediging van de wetenschap?
- Visualisatie van mechanische golven in een vloeibaar medium

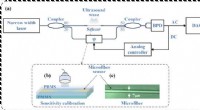
- Geminiaturiseerde, zeer gevoelige ultrasone sensor voor fotoakoestische beeldvorming
- Onverwachte hindernis ontdekken voor stellarator-fusiefaciliteiten

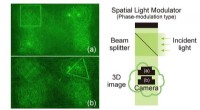
- Razendsnelle algoritmen kunnen de belasting van het genereren van 3D-hologrammen verlichten
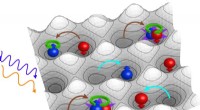
- Op weg naar een planetarium voor de kwantummetertheorie
 Een croquetbal van 0,50 kg bevindt zich aanvankelijk in rust op het gras wanneer het wordt getroffen door een gemiddelde kracht van de hamer die het 235 N uitoefende als snelheid na 3,1 ms hoe lang was de?
Een croquetbal van 0,50 kg bevindt zich aanvankelijk in rust op het gras wanneer het wordt getroffen door een gemiddelde kracht van de hamer die het 235 N uitoefende als snelheid na 3,1 ms hoe lang was de?  Nieuw interactief mozaïek maakt gebruik van NASA-beelden om Mars in levendige details weer te geven
Nieuw interactief mozaïek maakt gebruik van NASA-beelden om Mars in levendige details weer te geven  Wat gebeurt er als je een ei verwarmt?
Wat gebeurt er als je een ei verwarmt?  Opmerkelijke uitbarstingen vanuit het galactische centrum
Opmerkelijke uitbarstingen vanuit het galactische centrum Borstimplantaten markeren met tomaten-DNA om namaak te voorkomen
Borstimplantaten markeren met tomaten-DNA om namaak te voorkomen Kakkerlakkenboerderijen veranderen voedselafval in schatten
Kakkerlakkenboerderijen veranderen voedselafval in schatten  AEGIS op schema om vrije val van antimaterie te testen
AEGIS op schema om vrije val van antimaterie te testen Waarom voegen boeren kalksteen toe aan de bodem?
Waarom voegen boeren kalksteen toe aan de bodem?
- Elektronica
- Biologie
- Zonsverduistering
- Wiskunde
- French | Italian | Spanish | Portuguese | Swedish | German | Dutch | Danish | Norway |

-
Wetenschap & Ontdekkingen © https://nl.scienceaq.com

