
Wetenschap
Hoe berekent u de theoretische frequentie?
1. Begrijp het waarschijnlijkheidsmodel:
* Identificeer de verdeling: De theoretische frequentie hangt af van de waarschijnlijkheidsverdeling waarmee u werkt. Gemeenschappelijke verdelingen zijn de binomiale, Poisson-, normale en uniforme distributies.
* Ken de parameters: Elke verdeling heeft specifieke parameters die zijn vorm en gedrag bepalen. De binomiale verdeling heeft bijvoorbeeld de kans op succes (P) en het aantal proeven (N) nodig.
2. Bereken de waarschijnlijkheid van de gebeurtenis:
* Gebruik de waarschijnlijkheidsverdelingsformule: Elke verdeling heeft een formule die de waarschijnlijkheid van een specifiek resultaat berekent. U moet de relevante parameters aansluiten en het evenement waarin u geïnteresseerd bent.
* Voorbeeld: Als je een eerlijke munt hebt en de theoretische frequentie van het krijgen van koppen in 10 flips wilt weten, is de kans op koppen in een enkele flip 0,5 (p =0,5). U kunt de binomiale distributieformule gebruiken om de kans te berekenen om bijvoorbeeld precies 6 koppen te krijgen.
3. Vermenigvuldig de waarschijnlijkheid met het totale aantal waarnemingen:
* theoretische frequentie =waarschijnlijkheid * Aantal observaties
* Voorbeeld: Als u de munt 100 keer omdraait, zou de theoretische frequentie van het krijgen van 6 koppen de kans zijn om 6 koppen in 10 flips te krijgen vermenigvuldigd met 100.
Voorbeeld:binomiale verdeling
Stel dat u een munt hebt die 60% van de tijd kopt (p =0,6). Je draait het 20 keer om (n =20). Wat is de theoretische frequentie om precies 12 koppen te krijgen?
1. Binomiale waarschijnlijkheidsformule: P (x =k) =(nck) * p^k * (1 - p)^(n -k), waarbij nck de binomiale coëfficiënt is.
2. Bereken de kans: P (x =12) =(20C12) * 0.6^12 * 0.4^8 =0.1798 (ongeveer)
3. Theoretische frequentie: Als u dit experiment 100 keer uitvoert, zou de theoretische frequentie van het krijgen van 12 koppen 0.1798 * 100 =17,98 zijn. Je zou verwachten ongeveer 18 resultaten te krijgen met 12 hoofden in 100 proeven.
Sleutelpunten:
* theoretische frequentie is niet hetzelfde als waargenomen frequentie. Waargenomen frequentie is het werkelijke aantal keren dat een gebeurtenis plaatsvindt in een experiment.
* theoretische frequentie is gebaseerd op het onderliggende waarschijnlijkheidsmodel. Het is een theoretische voorspelling, geen garantie.
* Hoe dichter de waargenomen frequentie is bij de theoretische frequentie, hoe beter de pasvorm van het waarschijnlijkheidsmodel.
Laat het me weten als u een specifieker voorbeeld wilt of vragen heeft over het berekenen van theoretische frequenties voor een bepaalde verdeling.
Hoofdlijnen
- Hoe komen de spermacellen in een stuifmeelkorrel aan bij de eicelklus in een plant-ovule?
- Uit welk monomeer bestaat het enzym?
- Hoe is het segregatieprincipe van toepassing op bewegingschromosomen in meiose?
- Begrazing van vee schaadt leefgebied van reuzenpanda's
- Een ecologische afweging? Zonne-energie op nutsschaal belemmert bedreigde panters uit Florida
- Hoe cellen 'klimmen' om luchtpijpen van fruitvliegjes te bouwen
- Wat doet speeksel het eten?
- Hoe hersendood werkt
- Wat is de belangrijkste roofdier van Algaes?
- Natuurkunde kan nog steeds geen materie identificeren die het grootste deel van het universum vormt

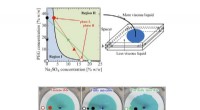
- Ontdekking van een nieuwe vloeistof-vloeistof grensvlakvervorming door gedeeltelijke mengbaarheid
- Nieuwe optische spectrometer voor het meten van atmosferische deeltjes

- Skyrmions kan gegevensopslag van de volgende generatie bieden

- Nieuwe methode gebruikt ruis om spectrometers nauwkeuriger te maken

 Hoe bepalen geologen het risico op aardbevingen?
Hoe bepalen geologen het risico op aardbevingen?  Fusion-onderzoekers onderschrijven het streven naar een proefcentrale in de VS
Fusion-onderzoekers onderschrijven het streven naar een proefcentrale in de VS De geheimen van wormen- en spinrag ontrafelen
De geheimen van wormen- en spinrag ontrafelen Wat is de zwaartekrachtpotentiaal energie van een microscoop met massa 0,49 kg op plank 1,6 m van de vloer?
Wat is de zwaartekrachtpotentiaal energie van een microscoop met massa 0,49 kg op plank 1,6 m van de vloer?  Apparaat brengt silicium rekenkracht naar hersenonderzoek en protheses
Apparaat brengt silicium rekenkracht naar hersenonderzoek en protheses Een ouderlijke paradox voor zwarte meisjes in het rechtssysteem
Een ouderlijke paradox voor zwarte meisjes in het rechtssysteem Tropisch bos ter grootte van Engeland vernietigd in 2018:rapport
Tropisch bos ter grootte van Engeland vernietigd in 2018:rapport Is het waar dat alle lichtgolven zich met verschillende snelheden in materialen voortbewegen?
Is het waar dat alle lichtgolven zich met verschillende snelheden in materialen voortbewegen?
- Elektronica
- Biologie
- Zonsverduistering
- Wiskunde
- French | Italian | Spanish | Portuguese | Swedish | German | Dutch | Danish | Norway |

-
Wetenschap © https://nl.scienceaq.com


