
Wetenschap
Wat is de relatie tussen rechtlijnige en cirkelvormige beweging?
rechtlijnige beweging:
* Definitie: Beweging langs een rechte lijn.
* Key -functies:
* Snelheid en versnelling zijn vectoren met richting langs de bewegingslijn.
* Eenvoudig te analyseren, vaak met constante snelheid of versnelling.
* Voorbeelden:een auto die over een rechte weg rijdt, een bal die verticaal valt.
Circulaire beweging:
* Definitie: Beweging langs een cirkelvormig pad.
* Key -functies:
* Snelheid is altijd raakzaam aan het cirkelvormige pad (richting verandert voortdurend).
* Versnelling is gericht op het midden van de cirkel (centripetale versnelling genoemd).
* Vereist een centripetale kracht om het cirkelvormige pad te behouden.
* Voorbeelden:een satelliet in een baan om de aarde, een bal vastgebonden aan een touw die in een cirkel slingert.
De relatie:
De belangrijkste verbinding ligt in het feit dat circulaire beweging kan worden gezien als een combinatie van twee rechtlijnige bewegingen . Hier is hoe:
1. Component van snelheid: Stel je een punt voor dat in een cirkel beweegt. Op elk moment kan de snelheid ervan worden ontleed in twee componenten:
* tangentiële component: Deze component is verantwoordelijk voor de beweging van het punt langs de omtrek van de cirkel.
* Radiale component: Deze component is nul omdat het punt niet naar of weg van het midden beweegt.
2. Component van versnelling: Evenzo kan de versnelling worden afgebroken in:
* Centripetale versnelling: Deze component wordt naar het midden gericht en houdt het punt in een cirkel bewegen.
* tangentiële versnelling: Deze component is verantwoordelijk voor elke verandering in de snelheid van de cirkelvormige beweging.
In wezen is cirkelvormige beweging een speciaal geval van rechtlijnige beweging waarbij de bewegingsrichting voortdurend verandert, wat resulteert in een gebogen pad.
Toepassingen:
Deze relatie heeft belangrijke implicaties op verschillende gebieden:
* ruimtevaartuigen: Het begrijpen van circulaire beweging is cruciaal voor het lanceren en onderhouden van satellieten in een baan.
* Roterende machines: Het analyseren van cirkelvormige beweging helpt ingenieurs om efficiënte motoren, turbines en andere roterende systemen te ontwerpen.
* Inzicht in planetaire beweging: Kepler's wetten van planetaire beweging zijn afhankelijk van de principes van circulaire beweging.
Conclusie:
Hoewel onderscheidend in hun paden, zijn rechtlijnige en cirkelvormige beweging onderling verbonden. Circulaire beweging kan worden opgevat als een meer complexe vorm van rechtlijnige beweging, waarbij de snelheidsrichting continu verandert. Deze relatie is van fundamenteel belang bij het begrijpen van verschillende fysieke fenomenen en technische toepassingen.
 Hoe klimaatverandering inheemse gemeenschappen beïnvloedt
Hoe klimaatverandering inheemse gemeenschappen beïnvloedt  Wanneer ontwikkeling en behoud botsen in de Serengeti
Wanneer ontwikkeling en behoud botsen in de Serengeti Hoe vogels hun vleugels kregen:Fossiele gegevens laten zien dat de schubben van ledematen zijn veranderd, afkomstig van dinosauriërs
Hoe vogels hun vleugels kregen:Fossiele gegevens laten zien dat de schubben van ledematen zijn veranderd, afkomstig van dinosauriërs  Atmosferische wetenschappers brengen het verlies van zee-ijs in de Noordpool in verband met sterke El Niño-gebeurtenissen
Atmosferische wetenschappers brengen het verlies van zee-ijs in de Noordpool in verband met sterke El Niño-gebeurtenissen  Klimaatverandering veroorzaakt een dramatische daling van de biodiversiteit en het visserijpotentieel van de Perzische Golf
Klimaatverandering veroorzaakt een dramatische daling van de biodiversiteit en het visserijpotentieel van de Perzische Golf
Hoofdlijnen
- Wat zijn de Charcteristics of Ambahan?
- Wat is de wetenschappelijke naam van rijst in Filipijns?
- Wat is in microbiologie het primaire gebruik van bouillons?
- Studie ontdekt hoe kankerverwekkende bacterie celdood stimuleert
- Intron: definitie, functie en belang bij RNA-splitsing
- Nieuw onderzoek laat zien hoe complex bonobo-communicatie vergelijkbaar is met die van menselijke baby's
- Wat controleert de biochemische routes van cellen?
- Wat is een vorm van genetische manipulatie waarin planten of dieren worden geselecteerd om te fokken en nakomelingen te geven met gewenste kenmerken die bekend staan?
- De sleutel tot het kweken van natuurlijk weefsel voor de reconstructie van het vrouwelijk voortplantingssysteem ontgrendeld
- Grafische kaartenboerderij om te helpen bij het zoeken naar nieuwe fysica bij LHCb

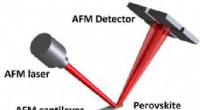
- Onderzoekers vinden eerste overtuigend bewijs van nieuwe eigenschap die bekend staat als ferroelasticiteit in perovskieten
- Elektronen breken rotatiesymmetrie in exotische supergeleider bij lage temperatuur

- Onderzoekers demonstreren labelvrije superresolutiemicroscopie

- Een lucifer op het toilet slaan helpt de PU te maskeren

 Wat vertegenwoordigt de stippellijn tussen watermoleculen?
Wat vertegenwoordigt de stippellijn tussen watermoleculen?  IJsbindende moleculen stoppen ijsgroei, fungeren als natuurlijke antivries
IJsbindende moleculen stoppen ijsgroei, fungeren als natuurlijke antivries Hoeveel elektronen in kwik?
Hoeveel elektronen in kwik?  Welke richting bekijkt u de aarde die wordt weergegeven door de cirkel?
Welke richting bekijkt u de aarde die wordt weergegeven door de cirkel?  Elektrische auto's:speciale kleurstoffen kunnen onnodige motorvervangingen voorkomen
Elektrische auto's:speciale kleurstoffen kunnen onnodige motorvervangingen voorkomen Wat is het doel van verwarming die in apparaten wordt gegenereerd?
Wat is het doel van verwarming die in apparaten wordt gegenereerd?  Nieuwe inzichten in hoe celmembranen de ontwikkeling van peptiden bij de ziekte van Alzheimer beïnvloeden
Nieuwe inzichten in hoe celmembranen de ontwikkeling van peptiden bij de ziekte van Alzheimer beïnvloeden  Welk instrument is verankerd op de grond en registreert de bewegingen van de aarde?
Welk instrument is verankerd op de grond en registreert de bewegingen van de aarde?
- Elektronica
- Biologie
- Zonsverduistering
- Wiskunde
- French | Italian | Spanish | Portuguese | Swedish | German | Dutch | Danish | Norway |

-
Wetenschap © https://nl.scienceaq.com

