
Wetenschap
Wat zijn de vergelijkingen van lineaire beweging alleen van toepassing als systeemversnelling?
De sleutelvergelijking
De meest fundamentele vergelijking voor lineaire beweging met constante versnelling is:
* v =u + bij
* v: Eindsnelheid
* u: Eerste snelheid
* a: Versnelling
* t: Tijd
afleiding en andere vergelijkingen
Deze vergelijking is afgeleid van de definitie van versnelling (a =ΔV/Δt) en uitgaande constante versnelling. Hieruit kunnen we andere nuttige vergelijkingen afleiden:
* s =ut + ½at² (Verplaatsing)
* v² =u² + 2AS (Relatie tussen snelheden en verplaatsing)
Waarom deze vergelijkingen alleen van toepassing zijn op versnelling
* Constante versnelling: De bovenstaande vergelijkingen zijn alleen geldig wanneer de versnelling constant is. Als de versnelling verandert, hebben we meer complexe calculus-gebaseerde methoden nodig.
* nulversnelling (constante snelheid): Als de versnelling nul is (wat betekent dat het object met een constante snelheid beweegt), vereenvoudigen de vergelijkingen aanzienlijk. De eerste vergelijking wordt bijvoorbeeld v =u, wat betekent dat de uiteindelijke snelheid gelijk is aan de beginsnelheid.
belangrijke overwegingen
* richting: Deze vergelijkingen zijn vectorvergelijkingen. Dat betekent dat u zich bewust moet zijn van de richting van de versnelling, snelheid en verplaatsing.
* Tekenconventie: Wees consistent met uw tekenconventie (bijvoorbeeld positief voor beweging rechts, negatief voor beweging naar links).
Voorbeeld
Laten we zeggen dat een auto begint vanaf rust (u =0 m/s) en 5 seconden versnelt op 2 m/s². We kunnen de vergelijkingen gebruiken om te vinden:
* Eindsnelheid (V): v =0 + (2 m/s²) (5 s) =10 m/s
* verplaatsing (s): S =(0 m/s) (5 s) + ½ (2 m/s²) (5 s) ² =25 m
Samenvattend zijn deze vergelijkingen van vitaal belang voor het beschrijven van lineaire beweging wanneer een object een constante verandering in snelheid ondergaat. Ze zijn de bouwstenen om meer complexe beweging te begrijpen.
 Waarom duiken plastic flessen in tijdens koud weer?
Waarom duiken plastic flessen in tijdens koud weer?  Plasticvrije campagnes hoeven niet te choqueren of te schamen. Shoppers zijn al aan boord
Plasticvrije campagnes hoeven niet te choqueren of te schamen. Shoppers zijn al aan boord Overweldigende internationale steun voor meer overheidsoptreden op milieugebied, bericht-test experiment vondsten
Overweldigende internationale steun voor meer overheidsoptreden op milieugebied, bericht-test experiment vondsten Wanneer water in een dunne laag over land stroomt, is dit dan?
Wanneer water in een dunne laag over land stroomt, is dit dan?  Gesteentemonsters suggereren dat de zuurstofniveaus tijdens het Lomagundi-evenement hoog genoeg waren om de voortgang van de levensontwikkeling te ondersteunen
Gesteentemonsters suggereren dat de zuurstofniveaus tijdens het Lomagundi-evenement hoog genoeg waren om de voortgang van de levensontwikkeling te ondersteunen
Hoofdlijnen
- Waar worden vezels gefermenteerd in het spijsverteringskanaal van varkens?
- Welk type organisme vormt de basis een piramide -getallen?
- De voedingsrelaties tussen planten en dieren die verschillende in een biotische gemeenschap worden genoemd, worden 1. Trofic 2. Biomassa 3. Symbiose 4. Niche 5. Voedselweb?
- Indringende vraag:Waarom overleefden zoogdieren het 'K/T-uitsterven'?
- Hoe creëer je een hypothese over wetenschappelijk probleem?
- Waar zijn stamcellen gevestigd?
- Wat zijn dunne Hread -achtige structuren gevonden in het cytoplasma van een cel?
- Hoe modificeren wetenschappers watermeloenen genetisch?
- Wat is de basis voor uitzonderingen op het Aufbau-principe?
- XENON1T-experimentele gegevens stellen de strengste limiet voor donkere materie vast

- Onderzoekers verbeteren algoritmen voor het leren van kwantummachines
- Team produceert unieke simulatie van magnetische herverbinding

- Nieuwe methode zorgt voor snelle, nauwkeurige meting van kwantumtoestanden

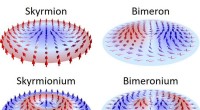
- Bimeronium:een nieuw lid van de familie van topologische spintexturen
 Hoe de natuurkunde de evolutie van medicijnresistentie verandert
Hoe de natuurkunde de evolutie van medicijnresistentie verandert  Waar is een aardbevingsvrije zone op aarde?
Waar is een aardbevingsvrije zone op aarde?  Wat is intellectuele energie?
Wat is intellectuele energie?  Hommels kunnen volgens de Californische instandhoudingswet als vissen worden geclassificeerd, zegt de rechtbank
Hommels kunnen volgens de Californische instandhoudingswet als vissen worden geclassificeerd, zegt de rechtbank Welke kracht werkt altijd op de verticale as?
Welke kracht werkt altijd op de verticale as?  Wat is de versnelling van een 2000 -kilogrammen vrachtwagen als Force 4200 N gebruikt om het vooruit te laten gaan?
Wat is de versnelling van een 2000 -kilogrammen vrachtwagen als Force 4200 N gebruikt om het vooruit te laten gaan?  Nieuwe grijswaardentechniek opent een derde dimensie voor lithografie op nanoschaal
Nieuwe grijswaardentechniek opent een derde dimensie voor lithografie op nanoschaal Dodelijke instorting van de dam in Brazilië roept angst op voor milieuproblemen
Dodelijke instorting van de dam in Brazilië roept angst op voor milieuproblemen
- Elektronica
- Biologie
- Zonsverduistering
- Wiskunde
- French | Italian | Spanish | Portuguese | Swedish | German | Dutch | Danish | Norway |

-
Wetenschap © https://nl.scienceaq.com

