
Wetenschap
Wat is de oorsprong van Fokker-Planck-vergelijking?
Hier is een uitsplitsing van zijn oorsprong:
1. Brownse beweging en Langevin -vergelijking:
* De fundering ligt in de observatie van Brownse beweging, de schijnbaar willekeurige beweging van deeltjes gesuspendeerd in een vloeistof.
* Albert Einstein en Marian Smoluchowski legde deze beweging uit met behulp van statistische mechanica, waaruit blijkt dat het wordt veroorzaakt door het continue bombardement van de deeltjes door de moleculen van de omliggende vloeistof.
* Paul Langevin Later geformuleerd een differentiaalvergelijking (Langevin -vergelijking) om de beweging van een deeltje te modelleren die onderworpen is aan zowel een deterministische kracht (bijvoorbeeld wrijving) als een willekeurige kracht.
2. Langevin verbinden met waarschijnlijkheid:
* De Langevin -vergelijking beschrijft het traject van een enkel deeltje. Om het collectieve gedrag van veel deeltjes te begrijpen, moeten we werken met waarschijnlijkheidsverdelingen.
* Andrey Kolmogorov en Adriaan Fokker Onafhankelijk ontwikkeld de Fokker-Planck-vergelijking door een probabilistische benadering van de Langevin-vergelijking toe te passen.
3. Afleiding:
* Ze gebruikten het idee van een diffusievergelijking , die de verspreiding van een stof beschrijft vanwege willekeurige beweging.
* Door de drift- en diffusietermen in de Langevin -vergelijking te overwegen, hebben ze een gedeeltelijke differentiaalvergelijking afgeleid die de tijdevolutie van de waarschijnlijkheidsdichtheidsfunctie regelt.
4. Belangrijkste bijdragen:
* Fokker gericht op het afleiden van de vergelijking aan een specifiek fysiek model, terwijl planck werkte aan zijn wiskundige kader.
* Kolmogorov Later generaliseerde de vergelijking om een bredere klasse van stochastische processen te beschrijven, wat leidde tot de naam Kolmogorov voorwaartse vergelijking.
In wezen overbrugt de Fokker-Planck-vergelijking de kloof tussen de deterministische beschrijving van individuele deeltjesbeweging (Langevin-vergelijking) en de probabilistische beschrijving van het collectieve gedrag van veel deeltjes (waarschijnlijkheidsdichtheidsfunctie).
Toepassingen:
De Fokker-Planck-vergelijking heeft wijdverbreide toepassingen op verschillende gebieden gevonden, waaronder:
* Natuurkunde: Brownse beweging, diffusieprocessen, plasmalysica
* chemie: Chemische kinetiek, reactiediffusiesystemen
* Biologie: Populatiedynamiek, genexpressie
* Financiën: Optieprijsmodellen, prijzen voor activa
Het is een krachtig hulpmiddel voor het begrijpen en voorspellen van het gedrag van systemen die onderworpen zijn aan willekeurige schommelingen.
 Onderzoek suggereert dat helium een oppasrol speelt bij het vormen van stabiele chemische verbindingen onder hoge druk
Onderzoek suggereert dat helium een oppasrol speelt bij het vormen van stabiele chemische verbindingen onder hoge druk Wat is een groep paar honderd chlorofyl B en carotenoïde moleculen die fungeren als lichte verzameleenheid die wordt genoemd?
Wat is een groep paar honderd chlorofyl B en carotenoïde moleculen die fungeren als lichte verzameleenheid die wordt genoemd?  Wat is het verschil tussen een thermodynamisch gunstige en ongunstige reactie?
Wat is het verschil tussen een thermodynamisch gunstige en ongunstige reactie?  Hoe verfijn je het oxidatiegetal in een reactie?
Hoe verfijn je het oxidatiegetal in een reactie?  Zijn deeltjes die dicht bij elkaar zijn in gasvloeistof of vaste stof?
Zijn deeltjes die dicht bij elkaar zijn in gasvloeistof of vaste stof?
 Biologen gebruiken de Sinatra-vlieg om te laten zien hoe je de blauwe en groene tinten ziet
Biologen gebruiken de Sinatra-vlieg om te laten zien hoe je de blauwe en groene tinten ziet  De winter is een belangrijke motor voor de uitstoot van lachgas uit boreale meren
De winter is een belangrijke motor voor de uitstoot van lachgas uit boreale meren Jouw duurzame voeding voor het jaar 2050:Meer noten, minder suiker en rood vlees
Jouw duurzame voeding voor het jaar 2050:Meer noten, minder suiker en rood vlees Wat zijn de eigenschappen van bijzondere eigenschappen?
Wat zijn de eigenschappen van bijzondere eigenschappen?  Klimaatverandering verandert de beschikbaarheid van terrestrisch water
Klimaatverandering verandert de beschikbaarheid van terrestrisch water
Hoofdlijnen
- Waarom heeft eencellig organisme geen systeem nodig voor transportmateriaal?
- Gedragswetenschap wordt zowel als een kunst beschouwd als uitleg?
- Hoe classificeerde John Ray organismen?
- Camponotini-mierensoorten hebben hun eigen verschillende microbiomen
- Waarom is het belangrijk in de wetenschap dat we tests ontwerpen en uitvoeren die in staat zijn om een hypothese te vervalsen?
- Studie meldt eerste bewijs van sociale relaties tussen chimpansees en gorilla's
- Wat zorgen voor koolhydraten voor de cel?
- Waarom was de uitvinding van microscoop belangrijk in studiecellen?
- Wat worden de gegevens weergegeven in een cel?
- Bewijs van verval van Higgs-deeltjes in quarks

- Onderzoekers ontwikkelen nieuw metamateriaal dat de MRI-kwaliteit kan verbeteren en de scantijd kan verkorten
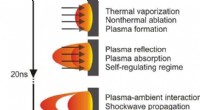
- High-fidelity simulaties wijzen de weg naar het optimaliseren van warmteoverdracht in huidige en volgende generatie reactoren

- Nieuwe ultrasnelle meettechniek laat zien hoe lasers beginnen vanuit chaos

- Hoe lasers kunnen helpen bij het monitoren van nucleaire non-proliferatie
 Ride-hailing verhoogt de afgelegde voertuigkilometers
Ride-hailing verhoogt de afgelegde voertuigkilometers Wat gebeurt er als de dichtheid van een vaste stof meer dan vloeistof is?
Wat gebeurt er als de dichtheid van een vaste stof meer dan vloeistof is?  Oceaancirculatie kan de sleutel zijn tot het vinden van leven op exoplaneten
Oceaancirculatie kan de sleutel zijn tot het vinden van leven op exoplaneten Wat is een diepe vallei met steile kanten onder de oceaan?
Wat is een diepe vallei met steile kanten onder de oceaan?  Hoeveel is 165 kilogram in ponden?
Hoeveel is 165 kilogram in ponden?  Zijn bacteriën hetzelfde als parasieten?
Zijn bacteriën hetzelfde als parasieten?  Hoe contragewichtgewichten te berekenen
Hoe contragewichtgewichten te berekenen Is er meer verbinding dan elementen?
Is er meer verbinding dan elementen?
- Elektronica
- Biologie
- Zonsverduistering
- Wiskunde
- French | Italian | Spanish | Portuguese | Swedish | German | Dutch | Danish | Norway |

-
Wetenschap © https://nl.scienceaq.com

