
Wetenschap
Hoe breuken af te trekken

Iedereen kan leren breuken aftrekken . Het is ongeveer net zo eenvoudig als het vermenigvuldigen van breuken, maar het aftrekkingsproces verschilt afhankelijk van het feit of de noemers van de twee breuken, of de onderste getallen, hetzelfde zijn.
Inhoud
- Breuken met dezelfde noemer aftrekken
- Breuken met ongelijke noemers aftrekken
- Veelgemaakte fouten die u moet vermijden bij het aftrekken van breuken
Breuken met dezelfde noemer aftrekken
Bij het aftrekken van getallen met een gelijke noemer (wat betekent dat hetzelfde getal onderaan beide breuken staat), is de berekening eenvoudig. Je trekt gewoon de tellers, of bovenste getallen, van elkaar af en houdt de twee noemers hetzelfde. Hier is een voorbeeld:
3/4 – 1/4 =2/4Wanneer de teller en de noemer een gemeenschappelijke deler hebben, vereenvoudigt u de breuk door de gemeenschappelijke deler te vinden en beide daardoor te delen. In het geval van 2/4 is de gemeenschappelijke factor 2, en de vereenvoudigde versie van 2/4 is 1/2.
Merk op dat 2/4 en 1/2 precies dezelfde hoeveelheid vertegenwoordigen.
Breuken met ongelijke noemers aftrekken
Stap 1:Vind de kleinste gemene deler
Bij het aftrekken van breuken met verschillende noemers is de eerste taak het vinden van een gemeenschappelijke noemer. Kijk naar de twee ongelijke noemers en zoek een getal dat een veelvoud is van beide, wat betekent dat het een getal is dat gelijkmatig door elk van de noemers kan worden gedeeld.
Stel dat we breuk B (2/5) aftrekken van breuk A (3/4):
3/4 – 2/5 =?
De noemer van breuk A is 4 en die van breuk B is 5, en we weten dat het kleinste gemene veelvoud van 4 en 5 20 is. Het is prima om tijdens het aftrekken een ander gemeenschappelijk veelvoud te gebruiken, zoals 40, maar het is gebruikelijk om de kleinste gemene deler (LCD), het kleinste getal dat voor beide noemers werkt.
Opmerking :Soms kom je een gemengd getal tegen (ook wel gemengde breuk genoemd), wat de combinatie is van een geheel getal en een echte breuk. Bij het aftrekken van gemengde breuken, zoals 2 1/2 – 1 3/4 , moet je de waarden omzetten in onechte breuken voordat je de kleinste gemene deler vindt. In dit voorbeeld wordt 2 1/2 5/2 en 1 3/4 7/4.
Stap 2:Converteer beide breuken
In een rekenkundige uitdrukking kun je elke breuk met 1 vermenigvuldigen; dat is altijd legaal.
Dus voor elke breuk wil je weten waarmee je de noemer kunt vermenigvuldigen om de kleinste gemene deler te krijgen bij het aftrekken van breuken. Dit cijfer heeft altijd dezelfde noemer als de andere breuk.
Omdat breuk A 4 als noemer heeft, moet je vermenigvuldigen met 5 – maar je kunt de noemer niet zomaar met 5 vermenigvuldigen. In plaats daarvan vermenigvuldig je de hele breuk met 5/5, wat gelijk is aan 1, en daarom eerlijk. spel. Je vermenigvuldigt breuk B met 4/4.
Hier ziet u hoe het eruit ziet om de twee ongelijke breuken om te zetten in breuken met een gemeenschappelijke noemer:
3/4 – 2/5 =[(5/5) x (3/4)] – [(4/4) x (2/5)] [(5/5) x (3/4)] – [ (4/4) x (2/5)] =15/20 – 8/20Stap 3:Trek de twee tellers af
Nu ben je klaar om de tellers af te trekken.
15/20 – 8/20 =7/20Er is geen vereenvoudiging nodig in dit probleem, omdat er geen gemeenschappelijke deler bestaat tussen 7 en 20.
Veelgemaakte fouten die u moet vermijden bij het aftrekken van breuken
Het aftrekken van breuken kan eenvoudig zijn, maar zelfs kleine fouten kunnen tot onjuiste antwoorden leiden. Hier zijn enkele veelvoorkomende fouten waar u op moet letten.
Met uitzicht op de gemeenschappelijke noemer
Een van de meest voorkomende fouten is het aftrekken van breuken met ongelijke noemers zonder eerst de LCD te vinden. Onthoud altijd dat breuken een gemeenschappelijke noemer moeten hebben om van elkaar afgetrokken te kunnen worden. Voor 2/3 − 4/5 is bijvoorbeeld een LCD van 15 nodig.
Verwarring van tellers met noemers
Houd na het uitlijnen van de noemers bij welke getallen de tellers zijn (boven) en welke de noemers (onder). Als u deze door elkaar haalt, kan dit leiden tot onjuiste aftrekkingen en een foutief resultaat.
Onjuiste behandeling van gemengde nummers
Het aftrekken van gemengde getallen zonder ze eerst om te zetten in onechte breuken is een recept voor fouten. 2 1/2 − 1 3/4 moet bijvoorbeeld worden omgezet naar 5/2 − 7/4, waarna een LCD wordt gevonden.
Breuken voortijdig vereenvoudigen
Weersta de verleiding om breuken te vereenvoudigen voordat u de aftrekking hebt uitgevoerd. Vereenvoudig alleen het uiteindelijke antwoord om er zeker van te zijn dat u geen gemeenschappelijke factoren over het hoofd hebt gezien.
Dit artikel is bijgewerkt in combinatie met AI-technologie, vervolgens op feiten gecontroleerd en bewerkt door een HowStuffWorks-editor.
Dat is interessantAls we het woord 'fractie' schrijven, komt het van het Latijnse fractus , wat 'kapot' betekent.
Veel beantwoorde vragen
Kun je twee breuken aftrekken?
Ja. Om twee breuken van elkaar af te trekken, zoek je een gemeenschappelijke noemer tussen de twee breuken en trek je de tellers ervan af.Kan ik breuken met verschillende noemers direct aftrekken?
Nee, je kunt breuken met verschillende noemers niet direct van elkaar aftrekken. Eerst moet je het kleinste gemene veelvoud (LCM) van de noemers vinden om ze hetzelfde te maken. Met deze gemeenschappelijke noemer kunt u de tellers op de juiste manier van elkaar aftrekken.Hoe trek ik gemengde getallen af?
Om gemengde getallen af te trekken, converteer je ze eerst naar onechte breuken. Hierbij wordt het gehele getal met de noemer vermenigvuldigd en de teller aan het resultaat toegevoegd. Zodra beide gemengde getallen zijn omgezet, gaat u verder met aftrekken zoals u dat met gewone breuken zou doen.Is er een snelle manier om breuken met dezelfde noemer af te trekken?
Wanneer u breuken met dezelfde noemer aftrekt, trekt u eenvoudigweg de tellers af en blijft de noemer ongewijzigd. Vereenvoudig vervolgens de resulterende breuk indien mogelijk.Wat moet ik doen als ik hierdoor een onechte breuk krijg?
Als uw aftrekking resulteert in een onechte breuk (waarbij de teller groter is dan de noemer), kunt u dit omzetten in een gemengd getal voor een duidelijkere weergave, of gewoon als een onechte breuk.Hoe vereenvoudig ik een breuk na het aftrekken?
Om een breuk te vereenvoudigen, zoekt u de grootste gemene deler (GGD) van zowel de teller als de noemer en deelt u beide door dit getal. Als er geen andere GCD is dan 1, heeft de breuk al de eenvoudigste vorm. Antacida helpt tuberculosebacteriën te overleven
Antacida helpt tuberculosebacteriën te overleven Onderzoeksteam ontwikkelt een draadloze sensor voor het opsporen van chemische oorlogsmiddelen
Onderzoeksteam ontwikkelt een draadloze sensor voor het opsporen van chemische oorlogsmiddelen  Snel, betrouwbare test voor besmetting met micro-organismen
Snel, betrouwbare test voor besmetting met micro-organismen Video:Hoe je onhandig met mensen in een bar omgaat met behulp van scheikunde
Video:Hoe je onhandig met mensen in een bar omgaat met behulp van scheikunde Hoe komt zure regen in de watercyclus?
Hoe komt zure regen in de watercyclus?
 natte winter, lente verlichten droogte in staat
natte winter, lente verlichten droogte in staat Vergelijkbare nettostraling tussen het hooggelegen Tibetaanse plateau en het laaggelegen Yangtze-riviergebied:studie
Vergelijkbare nettostraling tussen het hooggelegen Tibetaanse plateau en het laaggelegen Yangtze-riviergebied:studie  Arctisch zee-ijs bezwijkt voor Atlantificatie
Arctisch zee-ijs bezwijkt voor Atlantificatie Afbeelding:Portugal brandwonden littekens
Afbeelding:Portugal brandwonden littekens De effecten van donder en bliksem op mens en natuur
De effecten van donder en bliksem op mens en natuur
Hoofdlijnen
- Kenmerken van Animal-like Protists
- Drie van de meest bizarre relaties van de natuur
- Wat maakt een goede boer in Aotearoa?
- Termieten houden van het broeikaseffect, het tempo van hun houtkauwen wordt aanzienlijk sneller bij warmer weer
- Waarom onderzoekers geïnteresseerd zijn in het gezond houden van (sommige) koraalduivels
- Het herprogrammeren van bacteriën in plaats van ze te doden kan het antwoord zijn op antibioticaresistentie
- Wat zijn lobben in een kern?
- Een geïntegreerde beoordeling van vaatplantensoorten in Amerika
- Chimpansees bleken arm- en monduitdrukkingen te gebruiken om afstand over te brengen
- Spiegels gebruiken om de kwaliteit van lichtdeeltjes te verbeteren

- Fotonica-ontdekking voorspelt dramatische efficiëntie in siliciumchips
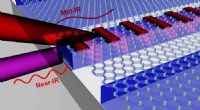
- Nieuw onderzoek draagt bij aan het werk van Prandtl, vader van de moderne aerodynamica

- Geminiaturiseerde, zeer gevoelige ultrasone sensor voor fotoakoestische beeldvorming
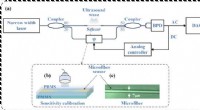
- Theoretisch model kan moleculair mysterie helpen oplossen
 Zeewater thuis repliceren
Zeewater thuis repliceren Polymeren voorkomen mogelijk gevaarlijke nevel tijdens tandartsbezoek
Polymeren voorkomen mogelijk gevaarlijke nevel tijdens tandartsbezoek Hoeveel sterrenlicht is er sinds het begin der tijden uitgestraald?
Hoeveel sterrenlicht is er sinds het begin der tijden uitgestraald?  In niet-vluchtige geheugentechnologieën kunnen 2D-materialen een grote sprong voorwaarts maken
In niet-vluchtige geheugentechnologieën kunnen 2D-materialen een grote sprong voorwaarts maken Houtafval transformeren voor duurzame productie
Houtafval transformeren voor duurzame productie  Welke soorten onzichtbare vlekken detecteren Black Lights?
Welke soorten onzichtbare vlekken detecteren Black Lights?  Nintendo lanceert in september een Switch Lite-console voor $ 200
Nintendo lanceert in september een Switch Lite-console voor $ 200 Onderzoekers ontwikkelen batterijloze chemische detector
Onderzoekers ontwikkelen batterijloze chemische detector
- Elektronica
- Biologie
- Zonsverduistering
- Wiskunde
- French | Italian | Spanish | Portuguese | Swedish | German | Dutch | Danish | Norway |

-
Wetenschap © https://nl.scienceaq.com

