
Wetenschap
Knoopjes in de resonator:elegante wiskunde in nederige natuurkunde

Een klaverknoop. Krediet:Wikipedia.
In het hart van elke resonator - of het nu een cello, een zwaartekrachtgolfdetector of de antenne in je mobiele telefoon is - zit een prachtig stukje wiskunde dat tot nu toe niet werd erkend.
Yale-natuurkundigen Jack Harris en Nicholas Read weten dit omdat ze knopen in hun gegevens begonnen te vinden.
In een nieuwe studie in het tijdschrift Nature , Harris, Read en hun co-auteurs beschrijven een voorheen onbekende eigenschap van resonatoren. Een resonator is elk object dat alleen op een bepaalde reeks frequenties trilt. Ze zijn alomtegenwoordig in sensoren, elektronica, muziekinstrumenten en andere apparaten, waar ze worden gebruikt om trillingen op specifieke frequenties te produceren, te versterken of te detecteren.
Het nieuwe kenmerk dat het Yale-team vond resultaten van vergelijkingen die elke middelbare school algebrastudent zou herkennen, maar die natuurkundigen niet hadden gewaardeerd als een basisprincipe van resonatoren.
Het is dit:als u een grafiek maakt van hoe de frequenties van de resonator veranderen terwijl u de resonator "afstemt" - door de eigenschappen ervan op bijna elke manier te variëren - toont de grafiek vlechten en knopen.
"De resonanties draaien om elkaar heen. Het is geweldig," zei Harris. "Het betekent dat elke keer dat je een instrument stemt, je een vlecht maakt. En als je het zo stemt dat je twee van de resonanties gelijk houdt, maak je een knoop."
Harris is een experimenteel natuurkundige. Zijn brood en boter onderzoekt de manieren waarop topologie en kwantummechanica geluid en licht beïnvloeden. Vaak voert hij experimenten uit met behulp van resonatoren die licht of geluid vangen in fysieke holtes.
Maar ondanks de hoogtechnologische aard van het werk, zijn er analogen met het werken met veel eenvoudigere instrumenten.
"Als je een viool aan het ontwerpen bent en je wilt weten hoe hij kan trillen, dan doe je hetzelfde als wij in mijn lab," zei Harris. "Het is de fysica van trillingen."
Een paar jaar geleden probeerde Harris enkele merkwaardige kenmerken te begrijpen die in zijn gegevens verschenen toen hij een holte afstemde. Hij wendde zich tot zijn collega Read, de Henry Ford II hoogleraar natuurkunde en hoogleraar toegepaste natuurkunde en wiskunde aan Yale.
Read legde uit dat deze kenmerken vlechten waren en gewoon uitdrukkingen waren van een fundamenteel wiskundig principe. "Maar toen hij uitlegde dat onze gegevens klaverknopen zouden moeten bevatten, was ik verslaafd", zei Harris.
Een klaverknoop is een figuur die in de iconografie van veel culturen voorkomt. Het is ook te vinden in het kunstwerk van M.C. Escher. Dit soort knopen zijn heel bekend bij wiskundigen, maar komen niet vaak voor in de natuurkunde.
Harris en Read ontwierpen een experiment waarin ze drie frequenties van een resonator afstemden en inderdaad de voorspelde vlechten en knopen observeerden.
De ontdekking, hoewel fundamenteel voor wiskunde, kan nuttig zijn voor natuurkundigen en ingenieurs. "Het is een potentieel krachtig hulpmiddel, wetende dat frequenties in een resonator kunnen vlechten," zei Harris. "Dat komt omdat een vlecht een topologisch object is, wat betekent dat het zijn essentiële karakter niet verandert als je het een beetje vervormt. Het blijft een vlecht tenzij je het echt verknoeit. Dit is een speciaal soort robuustheid waarvan we denken dat het kan worden gebruikt om fouten te voorkomen in toepassingen die afhankelijk zijn van het nauwkeurig afstemmen van resonatoren." + Verder verkennen
Het is eenrichtingsverkeer voor geluidsgolven in deze nieuwe technologie
 Redenen voor fouten in een chemie-experiment
Redenen voor fouten in een chemie-experiment  Lichtgevende gels voor een groot aantal toepassingen, van namaak tot bio-sensing
Lichtgevende gels voor een groot aantal toepassingen, van namaak tot bio-sensing De vonk die het leven schiep
De vonk die het leven schiep Wetenschappers ontwikkelen Venus flytrap-biosensoren om verontreinigende stoffen te vangen
Wetenschappers ontwikkelen Venus flytrap-biosensoren om verontreinigende stoffen te vangen Wetenschappers gebruiken koolstofnanobuistechnologie om robuuste ontziltingsmembranen voor water te ontwikkelen
Wetenschappers gebruiken koolstofnanobuistechnologie om robuuste ontziltingsmembranen voor water te ontwikkelen
 Met behulp van gegevens uit de echte wereld, wetenschappers beantwoorden belangrijke vragen over een atmosferische release
Met behulp van gegevens uit de echte wereld, wetenschappers beantwoorden belangrijke vragen over een atmosferische release Bescherming voor volle zee is cruciaal om kwetsbare kustgemeenschappen te beschermen - nieuw onderzoek
Bescherming voor volle zee is cruciaal om kwetsbare kustgemeenschappen te beschermen - nieuw onderzoek 8,3 miljard metrische ton:wetenschappers berekenen de totale hoeveelheid ooit geproduceerd plastic
8,3 miljard metrische ton:wetenschappers berekenen de totale hoeveelheid ooit geproduceerd plastic Hydrologische simulatiemodellen die beleidsbeslissingen informeren, zijn moeilijk te interpreteren
Hydrologische simulatiemodellen die beleidsbeslissingen informeren, zijn moeilijk te interpreteren Warmtevasthoudende koolstofdioxide in lucht bereikt nieuw record (update)
Warmtevasthoudende koolstofdioxide in lucht bereikt nieuw record (update)
Hoofdlijnen
- Waarom walvissen geen hersenbeschadiging oplopen als ze zwemmen
- Hersenonderzoek onthult hoe insecten de weg naar huis vinden
- Stropers richten zich op Afrikaanse leeuwen, gieren met vergif
- Helpers bij het nest kunnen moedervogels toestaan kleinere eieren te leggen
- Hoe nauwkeurig is ons mentale beeld van onszelf?
- Wat veroorzaakt DNA-mutatie?
- De wortels van biodiversiteit:hoe eiwitten verschillen tussen soorten
- Het redden van Indonesische paradijsvogels dorp voor dorp
- Hoe zal de aarde er over 50 uitzien,
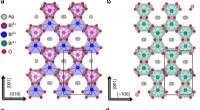
- Het beheersen van kwantuminteracties in een enkel materiaal
- Hollow-core vezels voor nauwkeurige positionering in de ruimte

- Wetenschappers ontdekken nieuwe manieren om licht te draaien en te verschuiven

- Magnetische stormen ontstaan dichter bij de aarde dan eerder werd gedacht, dreigende satellieten

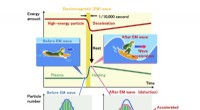
- Het proces van golven die plasmawarmte dragen, wordt voor het eerst waargenomen
 Berekening van CT-ratio
Berekening van CT-ratio  Een 3D-cel maken
Een 3D-cel maken Steden werpen schaduw bij stijgende hitte
Steden werpen schaduw bij stijgende hitte Feiten van kinderen over de Prairie Biome
Feiten van kinderen over de Prairie Biome  Team werpt nieuw licht op ontwerp van anorganische materialen voor hersenachtige computers
Team werpt nieuw licht op ontwerp van anorganische materialen voor hersenachtige computers Voedselkwaliteitscontrole sneller en gemakkelijker gemaakt
Voedselkwaliteitscontrole sneller en gemakkelijker gemaakt Google Earth onthult oude stenen poorten in Saoedi-Arabië
Google Earth onthult oude stenen poorten in Saoedi-Arabië Experts:overstromingen in Europa tonen noodzaak om emissies te beteugelen, aanpassen
Experts:overstromingen in Europa tonen noodzaak om emissies te beteugelen, aanpassen
- Elektronica
- Biologie
- Zonsverduistering
- Wiskunde
- French | Italian | Spanish | Portuguese | Swedish | German | Dutch | Danish | Norway |

-
Wetenschap © https://nl.scienceaq.com

