
Wetenschap
Snelheidslimieten voor kwantumverschijnselen zijn uitgebreid tot objecten van macroformaat
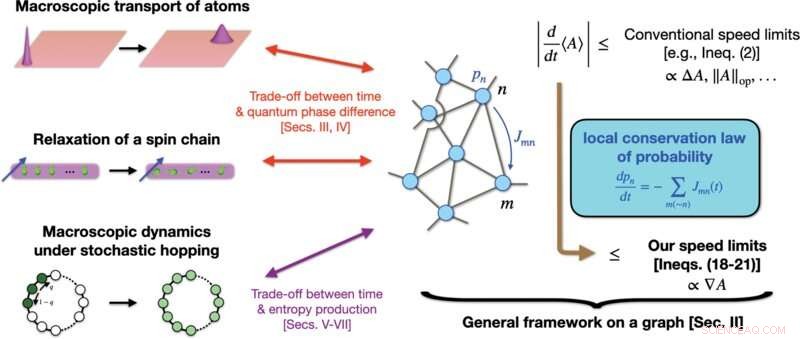
Schematische weergave van onze prestaties. We stellen een algemeen kader vast voor het afleiden van kwalitatief strakkere snelheidslimieten van een hoeveelheid A dan veel conventionele, die afhankelijk zijn van het hele bereik van A , zoals ΔA of ∥A ∥op . Onze strategie is om algemene dynamiek van ons belang in kaart te brengen met dynamiek in een grafiek, waarbij we de lokale behoud van waarschijnlijkheid gebruiken. In tegenstelling tot conventionele grenzen, hebben onze snelheidslimieten betrekking op de helling ∇A van A op de grafiek, die de grens aanzienlijk kan verscherpen wanneer ∇A ≪ΔA of ∥A ∥op . Wanneer toegepast op macroscopische kwantumsystemen (zoals macroscopisch transport van atomen of relaxatie van een lokaal verstoorde spinketen), wijst onze theorie op een nieuwe wisselwerking tussen tijd en het kwantumfaseverschil. Wanneer toegepast op macroscopische stochastische dynamiek, inclusief de kwantum, geeft onze theorie een wisselwerking aan tussen tijd en hoeveelheden, zoals de entropieproductie. Krediet:PRX Quantum (2022). DOI:10.1103/PRXQuantum.3.020319
Een uitdrukking voor de maximale snelheid waarmee veranderingen in macroscopische systemen kunnen optreden, is afgeleid door een theoretisch fysicus van RIKEN. Dit zal ons begrip van kwantumverschijnselen in systemen die niet in evenwicht zijn, verdiepen.
Een van de moeilijkst te begrijpen aspecten van de kwantummechanica is het onzekerheidsprincipe van Heisenberg dat stelt dat het niet mogelijk is om zowel de positie als het momentum van een object tegelijkertijd vast te stellen. Met andere woorden, hoe nauwkeuriger de positie van een deeltje wordt bepaald, hoe groter het bereik van zijn mogelijke impuls wordt (en vice versa).
In 1945 richtten twee natuurkundigen, Leonid Mandelstam en Igor Tamm, zich op een ander type van de onzekerheidsrelatie, namelijk die tussen tijd- en energiefluctuatie, en toonden aan dat overgangen in kwantumsystemen niet onmiddellijk plaatsvinden; in plaats daarvan wordt de snelheid waarmee een overgang plaatsvindt beperkt door een hoeveelheid die wordt bepaald door hoeveel de energie van het systeem fluctueert.
Er zijn vervolgens veel andere zogenaamde kwantumsnelheidslimieten afgeleid, die hebben bijgedragen aan een beter begrip van de fysica van kwantumsystemen en die nuttig zijn geweest in verschillende kwantumtoepassingen.
Maar er ontstaan grote problemen wanneer kwantumsnelheidslimieten worden toegepast op macroscopische systemen. "Vroegere kwantumsnelheidslimieten, die nuttig zijn voor kleine systemen, worden meestal zinloos voor macroscopische overgangen", merkt Ryusuke Hamazaki van het Nonquilibrium Quantum Statistical Mechanics RIKEN Hakubi Research Team op. "Bijvoorbeeld, conventionele kwantumsnelheidslimieten geven een oneindige bovengrens voor de snelheid van overgangen in een gas dat bestaat uit atomen."
Nu is Hamazaki erin geslaagd een kwantumsnelheidslimiet af te leiden voor overgangen in macroscopische systemen.
"Deze nieuwe afleiding biedt fundamentele limieten die kunnen worden toegepast op verschillende soorten niet-evenwichtige kwantummacroscopische verschijnselen", zegt hij. "Ik hoop dat veel fundamentele wetten en toepassingen met betrekking tot macroscopische kwantumdynamica zullen verschijnen op basis van de concepten die in deze studie zijn geïntroduceerd."
Hamazaki heeft de strengere kwantumsnelheidslimiet afgeleid door een algemeen raamwerk te ontwikkelen op basis van de behoudswet van waarschijnlijkheid, een fundamenteel principe in de natuurkunde.
Een onverwachte uitkomst voor Hamazaki was de ontdekking van een nieuwe ruilrelatie. "In plaats van een wisselwerking tussen tijd en energiefluctuatie, zoals in de Mandelstam-Tamm-grens, vond ik er een tussen tijd en de gradiënt van de kwantumfase - een fundamentele grootheid in de kwantumfysica."
Hamazaki is nu van plan zijn strategie uit te breiden om te zien of het kan worden gebruikt om kwantumsnelheidslimieten af te leiden voor grootheden zoals de groei van kwantumverstrengeling. + Verder verkennen
Quantum snelheidslimieten zijn niet echt quantum
 Alles samenvoegen:inspiratie voor taaie en zelfherstellende materialen
Alles samenvoegen:inspiratie voor taaie en zelfherstellende materialen Ultrastabiel, selectieve katalysator voor propaandehydrogenering ontwikkeld
Ultrastabiel, selectieve katalysator voor propaandehydrogenering ontwikkeld Nieuwe methode voor synthese van moleculaire waterstof stelt maatstaf voor platinavrije elektrokatalysatoren
Nieuwe methode voor synthese van moleculaire waterstof stelt maatstaf voor platinavrije elektrokatalysatoren Zonne-energie omzetten in waterstofbrandstof, met hulp van fotosynthese
Zonne-energie omzetten in waterstofbrandstof, met hulp van fotosynthese Computerprogramma's voor bio-informatica helpen biologen intrinsiek ongeordende eiwitten te begrijpen
Computerprogramma's voor bio-informatica helpen biologen intrinsiek ongeordende eiwitten te begrijpen
 Nieuw perspectief op de relatie tussen grootte en intensiteit van tropische cyclonen
Nieuw perspectief op de relatie tussen grootte en intensiteit van tropische cyclonen Detectie van hydrothermale bronnen in vulkanische meren
Detectie van hydrothermale bronnen in vulkanische meren Kikker-eieren zoeken
Kikker-eieren zoeken Ongekende niveaus van stikstof kunnen risico's opleveren voor het milieu op aarde
Ongekende niveaus van stikstof kunnen risico's opleveren voor het milieu op aarde Onderzoek naar platentektoniek herschrijft de geschiedenis van de continenten van de aarde
Onderzoek naar platentektoniek herschrijft de geschiedenis van de continenten van de aarde
Hoofdlijnen
- 3 fasen van interfase
- Hoe maak je een Bacterial Flowchart
- Wat is de levensduur van huidcellen?
- Hittetolerante broccoli voor de toekomst
- Bestudeer eerst om onkruidverdelger Roundup te koppelen aan stuiptrekkingen bij dieren
- Verschil tussen bacteriële en plantencelwand
- Hoe is een Cells DNA net als de boeken in een bibliotheek?
- Wat doet ethanol in een DNA-extractie?
- Ideeën voor Cookie Science Fair Projects
- Aansturen van ultrasterke licht-materie koppeling bij kamertemperatuur

- Spintronics:Giant Rashba-halfgeleiders vertonen een onconventionele dynamiek met potentiële toepassingen

- Upgrades leveren meer cryogeen vermogen op bij Large Hadron Collider

- Cartwheeling-licht onthult nieuw optisch fenomeen
- BASE opent nieuwe mogelijkheden in de zoektocht naar koude donkere materie

 Onderzoekers verkennen snoekbaarzen voor aquacultuur
Onderzoekers verkennen snoekbaarzen voor aquacultuur Hoe narcistische leiders van binnenuit vernietigen
Hoe narcistische leiders van binnenuit vernietigen Supercharged biomacromoleculen kunnen hun opnieuw geordende structuren behouden, bijvoorbeeld, door een vingertopaanraking
Supercharged biomacromoleculen kunnen hun opnieuw geordende structuren behouden, bijvoorbeeld, door een vingertopaanraking Genomics-onderzoek identificeert een unieke set eiwitten die het gehoor bij zebravissen herstellen
Genomics-onderzoek identificeert een unieke set eiwitten die het gehoor bij zebravissen herstellen Nieuw eenvoudig apparaat verbetert de analyse van de reactiekinetiek aanzienlijk
Nieuw eenvoudig apparaat verbetert de analyse van de reactiekinetiek aanzienlijk Deskundige wiskundigen stomverbaasd door eenvoudige aftrekkingen
Deskundige wiskundigen stomverbaasd door eenvoudige aftrekkingen Afgestudeerde student bedenkt nieuw voertuig voor het afleveren van kankermedicijnen
Afgestudeerde student bedenkt nieuw voertuig voor het afleveren van kankermedicijnen Hoe werkt een transducer?
Hoe werkt een transducer?
- Elektronica
- Biologie
- Zonsverduistering
- Wiskunde
- French | Italian | Spanish | Portuguese | Swedish | German | Dutch | Danish | Norway |

-
Wetenschap © https://nl.scienceaq.com

