
Wetenschap
De evolutie van Maxwell-knopen volgen
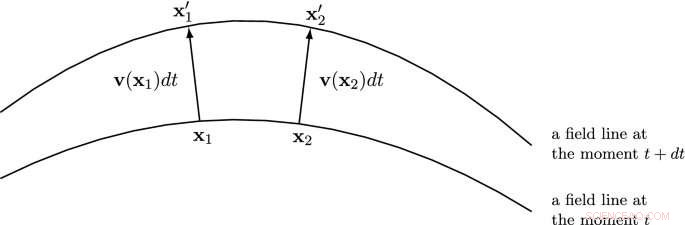
De afbeelding toont de voorwaarde waaraan het vectorveld v moet voldoen om de zelfconsistente tijdsevolutie van de veldlijnen te definiëren. Voor twee willekeurige punten op een veldlijn op het moment t liggen de uiteinden van de vectoren vdt op de corresponderende punten op een veldlijn die is gedefinieerd op het moment t+dt DOI 10.1140/epjc/s10052-020-08745-7
Maxwell-vergelijkingen bepalen de evolutie van elektromagnetische velden, waarbij licht een specifieke oplossing is van deze vergelijkingen in ruimten zonder elektrische lading. Een nieuwe studie gepubliceerd in EPJ C door Alexi Morozov en Nikita Tselousov, van het Moscow Institute of Physics and Technology en het Institute of Transmission Problems, Rusland, respectievelijk, geeft bijzondere oplossingen voor de Maxwell-vergelijkingen - de zogenaamde Maxwell-knopen. Het onderzoek kan toepassingen hebben op het gebied van wiskundige fysica en snaartheorie.
"We denken meestal aan licht als de vlakke golven. Het was een doorbraak toen 'geknoopte' lichtoplossingen werden ontdekt, " legt Tselousov uit. "De knoopaard van deze oplossing bestaat uit de structuur van de elektrische en magnetische veldlijnen. Je kunt zien dat sommige veldlijnen gesloten lussen zijn en niet-triviaal geknoopt."
Elektrische en magnetische veldlijnen veranderen in de loop van de tijd volgens de Maxwell-vergelijkingen. Terwijl de velden veranderen, bewegen hun veldlijnen op de een of andere manier in de ruimte. Hoewel onderzoekers geen willekeurige veldlijn kunnen volgen, gesloten veldlijnen zijn speciaal en kunnen worden waargenomen terwijl ze in de loop van de tijd evolueren.
"In onze krant we doen een vermoeden, dat geknoopte veldlijnen op een heel bijzondere manier bewegen waarbij de geknoopte structuur blijft, Tselousov gaat verder. Met andere woorden, men kan zeggen dat deze keer evolutie nooit zelfoverschrijdingen of kruisingen van twee veldlijnen inhoudt."
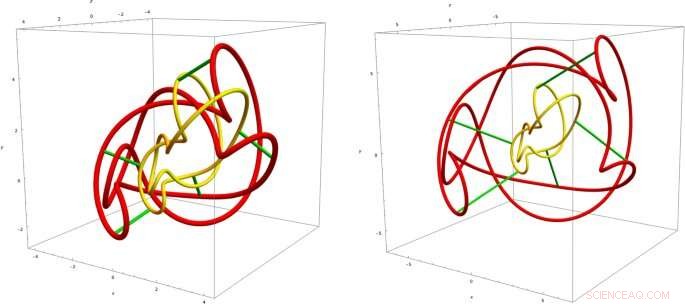
De kleine gele knoop wordt de grote rode onder tijdsevolutie. Er zijn foto's van twee opeenvolgende momenten in de tijd. De groene curven zijn de trajecten. De topologische structuur van knoop verandert niet onder de tijdsevolutie DOI 10.1140/epjc/s10052-020-08745-7
Tselousov is van mening dat als dit vermoeden - tot stand gekomen met behulp van complexe computersimulaties - correct zou zijn, het behoud van de knopen houdt in dat hun evolutie integreerbaar is - in staat om de wiskundige functie-integratie te ondergaan. Dit betekent dat de evolutie ervan gerelateerd kan worden aan andere modellen en systemen, in het bijzonder met niet-lineaire vergelijkingen, waarvan bekend is dat ze deze eigenschap delen.
"Het is zeer zeldzaam en altijd een plezier om de integreerbare eigenschappen van systemen te observeren, omdat het een dieper begrip en mogelijke verdere vooruitgang betekent. We zijn van plan om in deze richting te gaan en meer verbanden te vinden met integreerbaarheid, " Tselousov concludeert. "In mijn gedachten, een van de verbluffende feiten is dat licht, zo bekend bij iedereen, geheimen verbergen die we eeuwenlang negeerden."
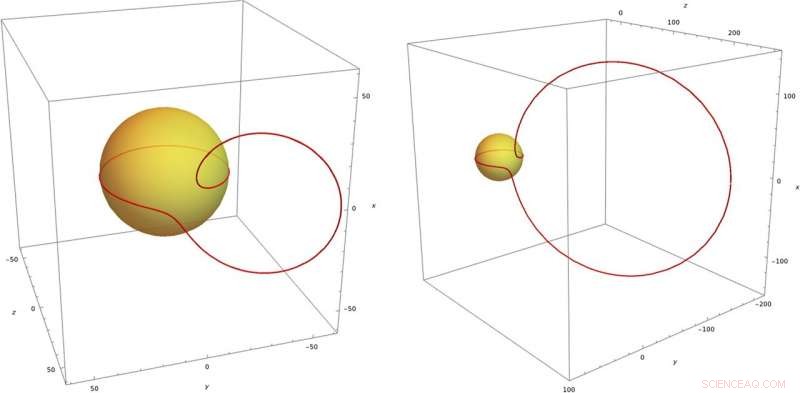
De gele bol is de lichtkegel x2+y2+z2=t2x2+y2+z2=t2. De rode lijnen zijn elektrische veldlijnen op het moment t=30t=30. Een deel van de veldlijn ligt op de evenaar van de bol. Het andere deel heeft de neiging een cirkel te vormen DOI 10.1140/epjc/s10052-020-08745-7
 Elektronenstraal versterkt recyclebaar nanocomposiet
Elektronenstraal versterkt recyclebaar nanocomposiet Een nieuwe strategie voor de synthese van complexe natuurlijke producten
Een nieuwe strategie voor de synthese van complexe natuurlijke producten Machine learning-software voorspelt gedrag van bacteriën
Machine learning-software voorspelt gedrag van bacteriën Nieuwe techniek kan helpen bij het ontwerpen van vervuild waterfilter, menselijke weefsels
Nieuwe techniek kan helpen bij het ontwerpen van vervuild waterfilter, menselijke weefsels Volgorde aanbrengen in, mRNA, of misschien nanokristallen? Wijd open veld voor Nobelprijs voor Scheikunde
Volgorde aanbrengen in, mRNA, of misschien nanokristallen? Wijd open veld voor Nobelprijs voor Scheikunde
Hoofdlijnen
- Hoe symbiose werkt
- Hadley Cell Effects
- Synthetische seks in gist belooft veiligere medicijnen voor mensen
- Wat hebben we geleerd van het Human Genome Project?
- Wetenschappers vinden antarctische microben die alleen van lucht leven
- Ontrafelen wat genomics kan doen
- Welke structurele rol spelen fosfolipiden in cellen?
- Hoe kolonies in de microbiologie te tellen
- Bij voetbalsucces draait alles om vaardigheid:studeren
- Optische technieken bieden snelle, efficiënte COVID-19-detectie

- Nieuwe aanpak kan HVAC-warmtewisselaars vijf keer efficiënter maken

- Hoe de hydraulische perskracht te berekenen in ton

- Praktisch anoniem communicatieprotocol ontwikkeld voor kwantumnetwerken

- Ultrasnelle kwantumsimulaties:een nieuwe draai aan een oude benadering

 Startup schaalt koolstof nanobuismembranen op om koolstofvrije brandstoffen te maken voor minder dan fossiele brandstoffen
Startup schaalt koolstof nanobuismembranen op om koolstofvrije brandstoffen te maken voor minder dan fossiele brandstoffen Voorbij LED's:helderder, nieuwe energiebesparende flatpanellampen op basis van koolstofnanobuisjes
Voorbij LED's:helderder, nieuwe energiebesparende flatpanellampen op basis van koolstofnanobuisjes Methaan in schorren
Methaan in schorren Onderzoekers ontdekken heetste lava die in de afgelopen 2,5 miljard jaar is uitgebarsten
Onderzoekers ontdekken heetste lava die in de afgelopen 2,5 miljard jaar is uitgebarsten Levering startup Instacart gewaardeerd op $ 7,6 miljard in financieringsronde
Levering startup Instacart gewaardeerd op $ 7,6 miljard in financieringsronde Onderzoekers kunnen nu eigenschappen van ongeordende polymeren voorspellen
Onderzoekers kunnen nu eigenschappen van ongeordende polymeren voorspellen Sprinkhaan springt op Bloch-bol en vindt nieuwe kwantuminzichten
Sprinkhaan springt op Bloch-bol en vindt nieuwe kwantuminzichten Is het een vogel? Is het een vliegtuig?
Is het een vogel? Is het een vliegtuig?
- Elektronica
- Biologie
- Zonsverduistering
- Wiskunde
- French | Italian | Spanish | Portuguese | Swedish | German | Dutch | Danish | Norway |

-
Wetenschap © https://nl.scienceaq.com

