
Wetenschap
Sprinkhaan springt op Bloch-bol en vindt nieuwe kwantuminzichten

Krediet:CC0 Publiek Domein
Nieuw onderzoek aan de Universiteit van Warwick heeft (excuseer de woordspeling) een nieuwe draai gegeven aan een wiskundige analogie met een springende sprinkhaan en zijn ideale gazonvorm. Dit werk zou ons kunnen helpen de spintoestanden van kwantumverstrengelde deeltjes te begrijpen.
Het sprinkhanenprobleem is bedacht door natuurkundigen Olga Goulko (toen bij UMass Amherst), Adrian Kent en Damián Pitalúa-García (Cambridge). Ze vroegen om de ideale gazonvorm die de kans zo groot mogelijk zou maken dat een sprinkhaan, beginnend vanaf een willekeurige positie op het gazon en een vaste afstand in een willekeurige richting springen, landt weer op het gazon. Intuïtief zou je verwachten dat het antwoord een cirkelvormig gazon is, tenminste voor kleine sprongen. Maar Goulko en Kent bewezen eigenlijk het tegendeel:verschillende vormen, van een tandradpatroon tot enkele losgekoppelde stukken gazon, presteerden beter voor verschillende spronggroottes (link naar de technische paper).
Naast verrassingen over gazonvormen en sprinkhanen, het onderzoek leverde nuttig inzicht op in ongelijkheden van het Bell-type met betrekking tot waarschijnlijkheden van de spintoestanden van twee gescheiden kwantumverstrengelde deeltjes. De Bell-ongelijkheid, bewezen door natuurkundige John Stewart Bell in 1964 en later op vele manieren gegeneraliseerd, toonde aan dat geen enkele combinatie van klassieke theorieën met de speciale relativiteitstheorie van Einstein de voorspellingen (en latere feitelijke experimentele waarnemingen) van de kwantumtheorie kan verklaren.
De volgende stap was om het sprinkhanenprobleem op een bol te testen. De Bloch-bol is een geometrische representatie van de toestandsruimte van een enkele kwantumbit. Een grote cirkel op de Bloch-bol definieert lineaire polarisatiemetingen, die gemakkelijk kunnen worden geïmplementeerd en vaak worden gebruikt in Bell en andere cryptografische tests. Vanwege de antipodale symmetrie voor de Bloch-bol, een gazon beslaat de helft van de totale oppervlakte, en de natuurlijke hypothese zou zijn dat het ideale gazon halfbolvormig is. Onderzoekers van de afdeling Computerwetenschappen aan de Universiteit van Warwick, in samenwerking met Goulko en Kent, onderzocht dit probleem en ontdekte dat het ook niet-intuïtieve gazonpatronen vereist. Het belangrijkste resultaat is dat het halfrond nooit optimaal is, behalve in het speciale geval dat de sprinkhaan precies een even aantal sprongen nodig heeft om rond de evenaar te gaan. Dit onderzoek toont aan dat er voorheen onbekende soorten Bell-ongelijkheden zijn.
Een van de auteurs van het artikel, Dmitry Chistikov van het Center for Discrete Mathematics and its Applications (DIMAP) en het Department of Computer Science, aan de Universiteit van Warwick, commentaar:
"Geometrie op de bol is fascinerend. De sinusregel, bijvoorbeeld, ziet er mooier uit voor de bol dan het vliegtuig, maar dit maakte ons werk niet gemakkelijk."
De andere auteur uit Warwick, Professor Mike Paterson FRS, zei:
"Sferische geometrie maakt de analyse van het sprinkhanenprobleem ingewikkelder. Dmitry, van de jongere generatie, gebruikte een leerboek uit 1948 en pen-en-papier berekeningen, terwijl ik mijn toevlucht nam tot mijn goede oude Mathematica-methoden."
De krant, getiteld "Globe-hopping, " is gepubliceerd in de Proceedings van de Royal Society A . Het is interdisciplinair werk waarbij wiskunde en theoretische natuurkunde betrokken zijn, met toepassingen op de kwantuminformatietheorie.
 Onderzoekers creëren grootste, langste multiphysics aardbevingssimulatie tot nu toe
Onderzoekers creëren grootste, langste multiphysics aardbevingssimulatie tot nu toe Onderzoekers ontdekken aanvullend bewijs voor enorme zonnestormen
Onderzoekers ontdekken aanvullend bewijs voor enorme zonnestormen Kunstmatige bodems kunnen de sleutel zijn bij het herstel van de kolenmijnen in Latrobe Valley
Kunstmatige bodems kunnen de sleutel zijn bij het herstel van de kolenmijnen in Latrobe Valley Nieuwe online tool toont klimaatverandering in je achtertuin
Nieuwe online tool toont klimaatverandering in je achtertuin Weer bovengemiddelde Atlantische orkaanactiviteit verwacht in 2021
Weer bovengemiddelde Atlantische orkaanactiviteit verwacht in 2021
Hoofdlijnen
- Wat is de meest logische volgorde van stappen voor het splitsen van vreemd DNA?
- Cellen voelen en verkennen hun omgeving
- Cephalization of Earthworms
- Wat zijn de niveaus van organisatie in de biologie?
- Met uitsterven bedreigde mus in Centraal-Florida die in het wild waarschijnlijk niet zal overleven
- Onderzoekers onthullen hoe stamcellen beslissingen nemen
- Wat zijn klaprozen?
- De locatie van Cilia en Flagella
- Verouderd DNA kan genen anders activeren
- Een nieuwe manier om laserinteracties te observeren, zou de op laser gebaseerde productie kunnen verbeteren
- Natuurkundige onderzoekt de mogelijkheid van overblijfselen van een universum voorafgaand aan de oerknal

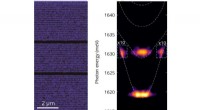
- Niet-lineaire effecten in gekoppelde optische microholtes
- Fragmenten van energie - geen golven of deeltjes - kunnen de fundamentele bouwstenen van het universum zijn

- Grote groepen fotonen op aanvraag - een equivalent van fotonisch geïntegreerd circuit

 Druk op Britse moslimouders om extremisme tegen te gaan is schadelijk
Druk op Britse moslimouders om extremisme tegen te gaan is schadelijk Lijst van zoogdieren in Tennessee
Lijst van zoogdieren in Tennessee STAR Detector onderweg
STAR Detector onderweg De polsslag van een vulkaan kan worden gebruikt om de volgende uitbarsting te voorspellen
De polsslag van een vulkaan kan worden gebruikt om de volgende uitbarsting te voorspellen Jeff Bezos schiet naar rijkste persoon ter wereld
Jeff Bezos schiet naar rijkste persoon ter wereld Wat is de oorzaak van magnetiseren?
Wat is de oorzaak van magnetiseren?  Reumatoïde artritis behandelen met micromotoren
Reumatoïde artritis behandelen met micromotoren Ceria-nanodeeltjes kunnen de schade door ischemische beroertes verminderen
Ceria-nanodeeltjes kunnen de schade door ischemische beroertes verminderen
- Elektronica
- Biologie
- Zonsverduistering
- Wiskunde
- French | Italian | Portuguese | Swedish | German | Dutch | Danish | Spanish | Norway |

-
Wetenschap © https://nl.scienceaq.com

