
Wetenschap
Het onderwijzen van natuurkunde aan neurale netwerken verwijdert chaosblindheid
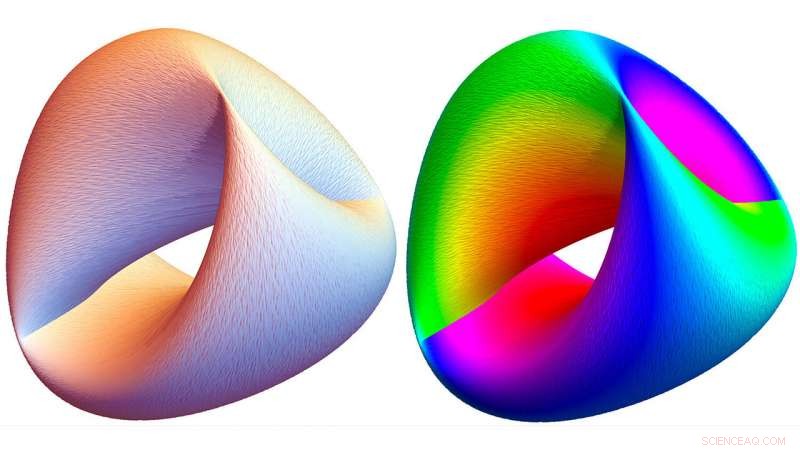
De Hamiltoniaanse stroom weergegeven als een donutachtige torus; regenboogkleuren coderen een vierde dimensie. Krediet:North Carolina State University
Onderzoekers van de North Carolina State University hebben ontdekt dat het aanleren van natuurkunde aan neurale netwerken die netwerken in staat stelt zich beter aan te passen aan de chaos in hun omgeving. Het werk heeft implicaties voor verbeterde toepassingen van kunstmatige intelligentie (AI), variërend van medische diagnostiek tot geautomatiseerde drone-piloten.
Neurale netwerken zijn een geavanceerd type AI dat losjes is gebaseerd op de manier waarop onze hersenen werken. Onze natuurlijke neuronen wisselen elektrische impulsen uit op basis van de sterke punten van hun verbindingen. Kunstmatige neurale netwerken bootsen dit gedrag na door numerieke gewichten en vooroordelen tijdens trainingssessies aan te passen om het verschil tussen hun werkelijke en gewenste output te minimaliseren. Bijvoorbeeld, een neuraal netwerk kan worden getraind om foto's van honden te identificeren door een groot aantal foto's te doorzoeken, raden of de foto van een hond is, zien hoe ver het is en dan zijn gewichten en vooroordelen aanpassen totdat ze dichter bij de realiteit zijn.
Het nadeel van deze neurale netwerktraining is iets dat 'chaosblindheid' wordt genoemd - een onvermogen om chaos in een systeem te voorspellen of erop te reageren. Conventionele AI is chaosblind. Maar onderzoekers van het Non-linear Artificial Intelligence Laboratory (NAIL) van NC State hebben ontdekt dat het opnemen van een Hamiltoniaanse functie in neurale netwerken hen in staat stelt om chaos binnen een systeem beter te "zien" en zich dienovereenkomstig aan te passen.
Simpel gezegd, de Hamiltoniaan belichaamt de volledige informatie over een dynamisch fysiek systeem - de totale hoeveelheid van alle aanwezige energieën, kinetisch en potentieel. Stel je een slingerende slinger voor, in de tijd heen en weer bewegen in de ruimte. Kijk nu eens naar een momentopname van die slinger. De momentopname kan u niet vertellen waar die slinger zich in zijn boog bevindt of waar hij vervolgens naartoe gaat. Conventionele neurale netwerken werken vanuit een momentopname van de slinger. Neurale netwerken die bekend zijn met de Hamiltoniaanse stroom begrijpen het geheel van de beweging van de slinger - waar het is, waar het zal of zou kunnen zijn, en de energieën die betrokken zijn bij zijn beweging.
In een proof-of-concept-project, het NAIL-team nam de Hamiltoniaanse structuur op in neurale netwerken, vervolgens toegepast op een bekend model van stellaire en moleculaire dynamica genaamd het Hénon-Heiles-model. Het Hamiltoniaanse neurale netwerk voorspelde nauwkeurig de dynamiek van het systeem, ook al bewoog het zich tussen orde en chaos.
"De Hamiltoniaan is echt de 'speciale saus' die neurale netwerken de mogelijkheid geeft om orde en chaos te leren, " zegt John Lindner, gastonderzoeker bij NAIL, hoogleraar natuurkunde aan The College of Wooster en corresponderende auteur van een paper waarin het werk wordt beschreven. "Met de Hamiltoniaan, het neurale netwerk begrijpt de onderliggende dynamiek op een manier die een conventioneel netwerk niet kan. Dit is een eerste stap in de richting van natuurkundig onderlegde neurale netwerken die ons kunnen helpen bij het oplossen van moeilijke problemen."
Het werk verschijnt in Fysieke beoordeling E en wordt gedeeltelijk ondersteund door het Office of Naval Research. NC State postdoctoraal onderzoeker Anshul Choudhary is eerste auteur. Bill Ditto, hoogleraar natuurkunde aan NC State, is directeur van NAIL. Bezoekend onderzoeker Scott Miller; Sudeshna Sinha, van het Indian Institute of Science Education and Research Mohali; en NC State afgestudeerde student Elliott Holliday droegen ook bij aan het werk.
 Het definiëren van de impact van orkaan Michael op St. Joe Bay, Florida
Het definiëren van de impact van orkaan Michael op St. Joe Bay, Florida Aqua Satellite vindt een meer georganiseerde, grote tropische storm Ampil
Aqua Satellite vindt een meer georganiseerde, grote tropische storm Ampil Nieuw onderzoek toont beschermende waarde van mangroven voor kustlijnen aan
Nieuw onderzoek toont beschermende waarde van mangroven voor kustlijnen aan Van marginale landbouwgronden winst maken voor boeren en ecosystemen
Van marginale landbouwgronden winst maken voor boeren en ecosystemen Sterke onderzeese aardbeving schudt Indonesië; geen tsunami-waarschuwing
Sterke onderzeese aardbeving schudt Indonesië; geen tsunami-waarschuwing
Hoofdlijnen
- Maak kennis met de kleine machines in cellen die virussen afslachten
- Onderzoekers rapporteren bevindingen over de controle van celdeling
- Hoe schimmels fruitvliegen manipuleren om sporen te ontvangen en vrij te geven?
- Franse regering verklaart de oorlog aan pesticiden
- Wat is een homologe eigenschap?
- Duizenden johannesbroodbomen geplant terwijl Cyprus het zwarte goud doet herleven
- Verschillen tussen een neuron en een neuroglia
- Het is wiskundig onmogelijk om veroudering te verslaan, wetenschappers zeggen:
- "DNA Model Project Ideas
- Optische chaos gebruiken om het momentum van licht te beheersen
- Gedetailleerde observatie van chemische processen met behulp van een tafellaser en speciale detector

- Nieuw inzicht in de stroom van polymeer en levende polymeeroplossingen
- Eerste willekeurige laser gemaakt van keramiek op papierbasis

- Studie observeert abnormaal verval van coherentie in een dissipatief veellichamensysteem
 De vormen van sterrenstelsels
De vormen van sterrenstelsels Sigarettenpeuken vormen een groot gevaar voor microplastics in de oceanen
Sigarettenpeuken vormen een groot gevaar voor microplastics in de oceanen Hooggerechtshof verwerpt beroep tegen netneutraliteit
Hooggerechtshof verwerpt beroep tegen netneutraliteit Waarom voedingskeuzes een impact hebben op de wereldwijde fauna en menselijke populaties
Waarom voedingskeuzes een impact hebben op de wereldwijde fauna en menselijke populaties NASA ziet wedergeboorte van tropische storm Paulette
NASA ziet wedergeboorte van tropische storm Paulette Een gemakkelijke manier om 's werelds dunste materiaal te zien
Een gemakkelijke manier om 's werelds dunste materiaal te zien Europa, Ruimtevaartuig klaar voor Japan voor 7-jarige reis naar Mercurius
Europa, Ruimtevaartuig klaar voor Japan voor 7-jarige reis naar Mercurius Nanostructureringstechnologie om tegelijkertijd warmte en elektriciteit te regelen
Nanostructureringstechnologie om tegelijkertijd warmte en elektriciteit te regelen
- Elektronica
- Biologie
- Zonsverduistering
- Wiskunde
- French | Italian | Spanish | Portuguese | German | Dutch | Danish | Norway | Swedish |

-
Wetenschap © https://nl.scienceaq.com

